Mémento géométrie
Profondeur d'une calotte sphérique
Volume d'une calotte sphérique
Les coniques
L'hyperbole
La parabole
Le cercle
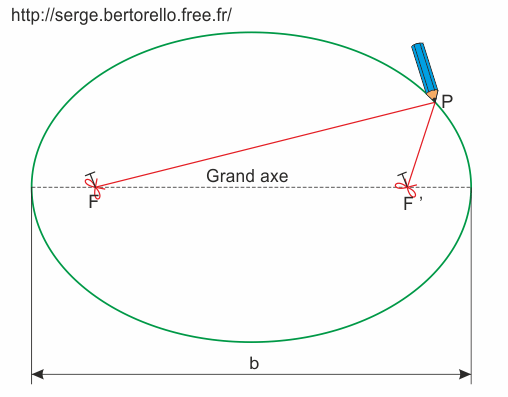
L'ellipse
Profondeur d'une calotte sphérique
On a souvent besoin de connaître cette valeur quand on fabrique une lentille ou un miroir pour maîtriser le rayon de courbure de sa surface.
En optique, on parle de la "flèche de courbure d'un miroir" pour désigner la profondeur de sa concavité.
La figure suivante montre le profil d'un miroir concave dont la surface épouse la forme d'une sphère de rayon R. On veut connaître la relation entre le rayon de la sphère R, le rayon du miroir H et la profondeur de la concavité p.

Voici tout d'abord des relations strictes :
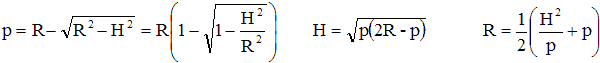
Voici maintenant des relations approchées qui sont suffisantes pour le calcul de concavité d'un miroir :

Exemple : Calculons la profondeur de la concavité d'un miroir de télescope de 200mm de diamètre et de 1000mm de distance focale. Dans ce cas nous avons :
H = 200 / 2 = 100mm
R = 2 x 1000 = 2000mm
L'emploi de la formule stricte nous donne :

L'emploi de la formule approchée nous donne :

Nous constatons que l'emploi de la formule approchée est suffisamment précis.
Volume d'une calotte sphérique
Nous voulons calculer le volume V d'une calotte sphérique de profondeur p et de rayon H (ce sont les notations précédentes).
Rappelons-nous que π = 3,1415926...

Exemple : Calculons la quantité de verre à enlever sur un disque de verre pour réaliser un miroir de 400mm de diamètre et de 1600mm de distance focale. Le paragraphe précédent nous permet de calculer la profondeur de l'usinage p = 6,256mm.

Ce calcul intéresse l'opticien qui va réaliser un miroir de télescope car le volume de la concavité à obtenir est proportionnel à la quantité d'abrasif nécessaire.
Les coniques
Les coniques sont des figures géométriques qui peuvent être définies comme l’intersection entre un cône de révolution et un plan.
Un cône de révolution est une surface engendrée par la rotation d'une ligne droite (la génératrice) autour d'une autre ligne droite (l'axe du cône) avec un angle constant entre elles. Ces deux lignes sont sécantes, elles se coupent au sommet du cône.
Comme on peut le voir sur la figure ci-contre, le cône possède deux composantes symétriques mais on évoque souvent une seule d'entre-elles.
L'hyperbole
L'hyperbole est l'intersection entre un cône de révolution et un plan orienté entre la direction de l'axe du cône et celle de sa génératrice.
Dans le cas de la figure ci-contre, ce plan est parallèle à l'axe du cône.
L'image de droite montre la portion du plan avec la trace hyperbolique (en rouge) de son intersection avec le cône.
La parabole
La parabole est l'intersection entre un cône de révolution et un plan parallèle à une direction de sa génératrice.
L'image de droite montre la portion du plan avec la trace parabolique (en rouge) de son intersection avec le cône.