Mémento trigonométrie
Trigonométrie plane : fonctions de base
Aire d'un triangle
Trigonométrie sphérique
Trigonométrie plane : fonctions de base
La connaissance des fonctions trigonométriques est très utile pour étudier les triangles, les cercles et les fonctions périodiques. Il existe six fonctions trigonométriques de base mais le sinus, le cosinus et la tangente sont de loin les plus employées et c'est surtout sur elles que nous porterons notre attention. Nous allons définir ces fonctions de deux façons.
Définitions à partir du cercle trigonométrique :
Soit un repère orthonormé dans le plan euclidien, le cercle trigonométrique est le cercle de rayon 1 dont le centre est l'origine du repère.
Soit un point M de ce cercle. Le rayon qui passe par M fait un angle θ avec l'axe horizontal (x).
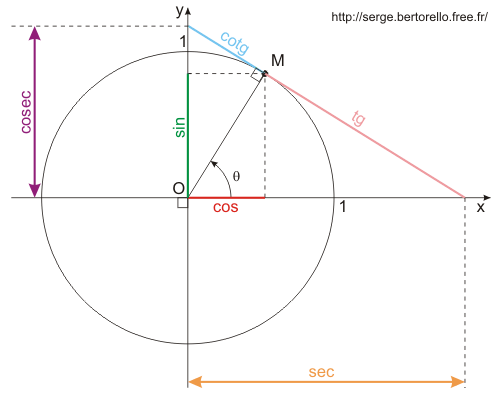
La figure ci-contre montre chacune des fonctions de base sous la forme d'un segment de droite qui possède une longueur égale à la valeur de la fonction correspondante.
Rappelons le nom de ces fonctions trigonométriques de base et leurs abréviations :
Cosinus (cos)
Tangente (tg, tan ou tang)
Cotangente (cotg, cotan ou cot)
Sécante (sec ou séc)
Cosécante (cosec ou coséc ou csc) Définitions sur un triangle rectangle :
Considérons un triangle ABC qui est rectangle en B et rappelons quelques définitions :
L'hypoténuse du triangle rectangle est le côté opposé à l'angle droit, ici c'est le côté b.
Le côté a est le côté opposé à l'angle A.
Le côté c est le côté adjacent à l'angle A. Sinus : Le sinus d'un angle est le rapport de la longueur du côté opposé à la longueur de l'hypoténuse.
Pour désigner le sinus de l'angle A, on peut écrire sin(A) ou sin A :
Cosinus : Le cosinus d'un angle est le rapport de la longueur du côté adjacent à la longueur de l'hypoténuse.
Pour désigner le cosinus de l'angle A, on peut écrire cos(A) ou cos A :
Tangente : La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent.
Pour désigner la tangente de l'angle A, on peut écrire tg(A) ou tg A :
On peut déterminer la valeur de la tangente d'un angle à partir de son sinus et de son cosinus :
Application du théorème de Pythagore :
Quel que soit l'angle θ, nous avons :
Unités d'angle :
Dans le langage commun on mesure habituellement les angles en degrés (°). Il faut 360° pour un tour complet.
Dans le langage des physiciens on mesure les angles en radians (rad). C'est une convention internationale définie dans le Système International d’unités - le SI.
Un angle de 1 rad est un angle qui, ayant son sommet au centre d'un cercle, intercepte, sur la circonférence de ce cercle, un arc d'une longueur égale à celle du rayon du cercle.
Souvent quand on exprime les angles en radians en fraction de π, on ne précise pas l'unité.
1 rad = 57,2958°
Il faut donc 2π radians pour faire un tour.
π rad équivaut à un angle plat de 180°.
Un angle droit (90°) vaut π/2.
Dans un espace euclidien :
L'équation suivante est valable pour tous les triangles, à condition qu'ils soient définis dans un espace euclidien. Cette égalité caractérise l'espace considéré et sa vérification permet de confirmer son caractère euclidien.
Autrement dit, la somme des angles d'un triangle quelconque est toujours égale à 180° (ou π radians).
Ainsi, quand on considère notre univers dans ses plus grandes dimensions, cette égalité n'est plus exacte. C'est la conséquence de la courbure de l'espace comme l'a exprimé en 1851 le mathématicien allemand Bernhardt Riemann (1826 - 1866).
Quelques valeurs particulières à retenir par cœur...

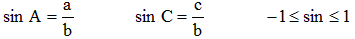



cos2 θ + sin2 θ = 1

A + B + C = 180° = π
avec A, B, C qui sont les trois angles du triangle.
| Angle | 0 | 30° ou π/6 | 45° ou π/4 | 60° ou π/3 | 90° ou π/2 |
| sin | 0 | 0,5 |  |
 |
1 |
| cos | 1 |  |
 |
0,5 | 0 |
| tg | 0 |  |
1 |  |
indéfinie |

L'aire "A" un triangle (ou sa surface), dans le plan euclidien, est égale à la moitié du produit de la longueur de sa base par sa hauteur :

Pour ce calcul, on prend un côté quelconque du triangle qu'on désigne comme sa base "b". La hauteur "h" est la longueur du segment de droite qui est perpendiculaire à la base et qui passe par son troisième sommet (celui qui n'appartient pas à la base).
L'illustration ci-contre montre un exemple de triangle dont l'aire est colorée en bleu.
On aurait pu prendre comme base un des deux autres côtés et la hauteur correspondante, le résultat du calcul de l'aire aurait été exactement le même.
La figure suivante montre des triangles qui ont la même longueur de base et la même hauteur. Ils ont donc tous une aire de même valeur. Notez au passage que, dans certains cas, la hauteur doit être mesurée à l'extérieur du triangle.

Observons cette dernière figure. Les différents triangles ont été obtenus à partir du premier en faisant simplement glisser le point "B" sur une ligne parallèle à la base comme le montre l'animation suivante.
Cette pratique est parfois utile pour résoudre des problèmes géométriques...

La trigonométrie sphérique étudie les angles des triangles sphériques. Un triangle sphérique est la surface limitée sur une sphère par trois grands cercles joignant trois points de cette sphère.
Cette discipline est très utile en astronomie car le repérage des astres se fait sur la "sphère céleste". En effet, nous pouvons considérer que nous sommes situés au centre d'une sphère sur la surface de laquelle sont positionnés les astres. Dans ce cas, la distance n'intervient pas.

Les grands cercles sont tracés sur la sphère et ont le même centre qu'elle. Ainsi, chaque grand cercle divise la sphère en deux parties égales. Les grands cercles sont des géodésiques. Cela signifie que, si nous considérons deux points d'une sphère, l'arc de cercle le plus court qui les joint appartient au grand cercle qui les contient.
Les côtés d'un triangle sphérique sont les longueurs des arcs qui limitent sa surface, le rayon de la sphère étant pris pour unité, ce sont donc des angles.
La figure ci-contre illustre en bleu l'aire d'un triangle simple. On le qualifie ainsi car tous ses côtés sont plus petits qu'une demi-circonférence. Cela signifie que la définition du triangle sphérique admet qu'on considère le triangle autrement. Ainsi, par exemple, nous aurions pu considérer que le côté BC du triangle ne soit pas l'arc b mais l'autre partie du grand cercle qui passe par B et C.
Il y a en tout 8 triangles distincts définis par trois points.
Dans ce qui va suivre, nous considérerons uniquement les triangles simples.
Nous utiliserons les lettres minuscules pour désigner les côtés du triangle et les lettres majuscules pour désigner indifféremment les sommets ou les angles des sommets.
Le côté "a", opposé à l'angle "A", est un arc de cercle défini par l'angle BOC.
De même, le côté "b", opposé à l'angle "B", est un arc de cercle défini par l'angle AOC.
Et le côté "c", opposé à l'angle "C", est un arc de cercle défini par l'angle AOB.
Propriétés
La somme des angles d'un triangle sphérique est toujours supérieure à 180° (ou π) :
Notons au passage que la différence entre cette somme et π nous permet de calculer l'aire A du triangle sphérique :
- A = (A + B + C - π) . R2
avec : R = rayon de la sphère
Par ailleurs, voici les relations remarquables :
- sin a . cos B = cos b . sin c - sin b . cos c . cos A
sin a . sin B = sin b . sin A
cos a = cos b . cos c + sin b . sin c . cos A
cos A = - cos B . cos C + sin B . sin C . cos a
sin A . cos b = cos B . sin C + sin B . cos C . cos a
A partir de ces relations, on peut déduire les autres équations par simple permutation des lettres.
Exemple d'application : Calcul de la séparation angulaire entre deux astres de coordonnées connues :
Considérons la figure précédente dans laquelle nous attribuons la position du pôle céleste Nord au point A. Les deux astres considérés sont placés respectivement sur les points B et C et leur séparation angulaire est a.
Dans ces conditions, nous pouvons dire que :
- c = 90° - déclinaison de B (puisque c est la distance angulaire entre B et le pôle A)
b = 90° - déclinaison de C (puisque b est la distance angulaire entre C et le pôle A)
A = ascension droite de C - ascension droite de B
La séparation angulaire recherchée est alors obtenue en appliquant la formule :
- cos a = cos b . cos c + sin b . sin c . cos A

