"Le savoir que l'on n'enrichit pas chaque année s'appauvrit tous les ans"
LAO TSEU (VI et V siècle avant JC)
Nombreux sont ceux qui apprécient l'astronomie sans avoir la moindre expérience des mathématiques. Pour un amateur cela n'est pas très important, les mathématiques sont des outils qui permettent aux spécialistes de mieux comprendre l'univers. On peut trouver du plaisir à pratiquer l'astronomie sans mathématiques, de même que l'on peut aimer les meubles sans être menuisier.
Hélas quelques portes restent désespérément fermées à celui qui n'est pas "matheux". Il aura du mal, par exemple, à calculer sa configuration optique ou le bulletin de contrôle de son miroir, à déterminer le temps de pose correct pour certaines photographies ou bien à comprendre la loi de la gravitation universelle.
L'exposé qui va suivre est destiné à ceux qui sont dans ce cas et qui souhaitent acquérir les quelques notions les plus utiles, sans trop entrer dans le détail. Il ne s'agit pas d'un cours de mathématiques rigoureux mais de quelques notions faisant appel à l'intuition du lecteur. Nous effectuerons ensuite quelques exercices simples et concrets qui montreront l'utilité de ces rudiments.
Ainsi, nous avons voulu répondre aux questions que beaucoup n'osent pas poser.
Ce qui surprend souvent les non-initiés lorsqu'ils lisent une formule mathématique, telle que la loi de la gravitation universelle, c'est qu'elles sont coupées en deux par un trait horizontal. Celui-ci signifie que la partie du haut, appelée numérateur, est divisée par la partie du bas, le dénominateur. Ce trait symbolise la division comme les deux points qui sont encore utilisés.
Parfois, ce trait de fraction peut être un trait incliné.
Exemple :
L'expression 
est équivalente à 3:5 et à 3/5. Elle signifie "trois divisé par cinq"
Dans une formule, certaines expressions peuvent être regroupées entre 2 parenthèses. Celles-ci isolent une partie de la formule qui doit être calculée séparément. Les parenthèses vont par couple, à une parenthèse ouvrante "(" correspond obligatoirement une parenthèse fermante ")".
Exemple :
est équivalent
à (3+7) divisé par (5x4) = (3+7):(5x4) = 10:20
= 0,5
Dans une formule, le point est le signe de la multiplication, il équivaut au signe "x".
Ainsi 3.5 est équivalent à 3x5 "trois multiplié par cinq".
Hélas, cet aspect est compliqué par le fait que les Anglo-saxons utilisent le point comme séparateur décimal. Dans ce cas, il est l'équivalent de notre virgule. Ainsi 3.5 pour un anglais ou un américain correspond à 3,5 pour un français.
Une formule mathématique est composée de lettres. Cela ne veut pas dire que l'on peut faire des opérations arithmétiques sur des lettres. On ne pourra jamais diviser une lettre A par une lettre B ! Ces lettres servent à remplacer des nombres connus ou inconnus qui seraient difficiles à manipuler.
Ainsi on utilise habituellement la lettre grecque π (lire "pi") pour désigner le rapport entre la circonférence et le diamètre du cercle. Dans ce cas là, π est une constante dont on connaît bien la valeur. π = 3,1415926... . On prend en compte un nombre plus ou moins grand de chiffres après la virgule selon la précision souhaitée pour le calcul.
Considérons la formule suivante, elle définit le périmètre (ou la circonférence) du cercle en fonction du diamètre :
P = π. D
Nous avons choisi arbitrairement d'affecter la lettre D au diamètre du cercle et la lettre P à son périmètre. Le point qui sépare π et D est le signe de la multiplication. Cette formule indique que le périmètre d'un cercle est égal au résultat de la multiplication de π par son diamètre.
Exemple :
Calculons le périmètre d'un cercle de 2 mètres de diamètre.
Appliquons la formule : P = π . D
Nous savons que π = 3,14 et que D = 2m
donc P = 3,14 x 2 = 6,28m
Il ne s'agit pas d'une figure géométrique. Le carré d'un nombre est la multiplication de ce nombre par lui-même, il se note par un petit chiffre 2 placé en haut et à droite de ce nombre.
Exemple :
b² se lit "b au carré", cela équivaut à b.b
b² = b x b = b.b "b au carré égale b que multiplie b"
Autres exemples
2² = 4 3² = 9
5² = 25
Il ne s'agit toujours pas d'une figure géométrique. Le cube d'un nombre est la multiplication de ce nombre par son propre carré, il se note de la même façon par un petit chiffre 3.
Exemple :
b³ se lit "b au cube", cela équivaut à b.b²
on peut aussi écrire
b³ = b.b.b "b au cube
égale b que multiplie b que multiplie b"
Autres exemples
2³ = 8 3³ = 27
5³ = 125
La racine carrée
La racine carrée est symbolisée par le signe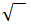 
sous lequel se trouve l'expression dont on doit extraire la racine carrée.
"racine carrée de quatre égale deux"
La racine carrée n'est pas toujours un nombre entier (un nombre entier est dépourvu de chiffres après la virgule). Ainsi la racine carrée de 2 vaut 1,4142... . On prend en compte un nombre plus ou moins grand de chiffres après la virgule selon la précision souhaitée pour le calcul.
Exemples :
"racine carrée de six plus trois égale racine carrée de neuf égale trois"
En multipliant un nombre par lui-même on obtient son carré, on dit aussi qu'on l'élève à la puissance deux. Ainsi 2² se lit aussi "deux élevé à la puissance deux". Nous avons vu quelques exemples de puissances, le cube est la puissance trois et la racine carrée est la puissance 0,5.
On note :
"racine carrée de b égale b élevé à la puissance 0,5"
L'exposant est ce petit chiffre en haut et à droite du nombre considéré. Cette notion peut être généralisée, on peut donc rencontrer n'importe quelle valeur comme exposant.
Notez bien les cas suivants :
"b élevé à la puissance un égale b lui-même"
En effet, élever un nombre à la puissance un ne le modifie pas.
Quel qu'il soit, un nombre non nul élevé à la puissance zéro égale un.
La connaissance des puissances est très utile, surtout lorsqu'elles concernent le nombre 10.
Comment pouvons-nous écrire l'âge de l'univers? Actuellement nous admettons qu'il est âgé de quinze milliards d'années, c'est à dire 15 000 000 000 d'années (quinze suivi de neuf zéros). Ce nombre est difficile à manipuler.
Un milliard égale dix à la puissance neuf (109), ou si vous préférez :
1 000 000 000 = 109 = 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10
Il est donc plus commode d'écrire que l'âge de l'univers vaut quinze fois dix à la puissance neuf :
Age de l'univers = 15.109 années
L'exposant du dix est égal au nombre de zéros qui suivent le un dans la notation classique. Ainsi nous avons :
10 = 101 100 = 102 1000 = 103 10 000 = 104 etc...
Les puissances de dix peuvent être négatives :
10-1 = 0,1 10-2 = 0,01 10-3 = 0,001 etc...
Dans ce dernier cas l'exposant du dix est égal au nombre de zéros qui précèdent le un en comptant aussi celui qui est avant la virgule.
Exemples :
1mm = 10-3m "un millimètre égale dix à la puissance moins trois mètre"
Un micromètre (populairement on dit un micron) se note μm et vaut un millionième de mètre ou un millième de millimètre :
1μm = 10-6m = 10-3mm "un micromètre égale dix à la puissance moins six mètre et égale dix à la puissance moins trois millimètre"
La longueur d'onde de la lumière Hα
( H alpha) de l'hydrogène est de 0,656 μm ou 0,656.10-6 mètre.
1. Nous savons calculer le périmètre d'un cercle à partir de son diamètre (voir plus haut). Supposons maintenant que nous connaissons le périmètre d'un cercle et que nous voulons en déduire le diamètre. Nous pouvons modifier la formule que nous avons vue précédemment, elle devient :
Calculez le diamètre d'un cercle dont le périmètre vaut 2872mm.
Solution :
Ceci est très précisément le diamètre du secteur d'entraînement du télescope de 400mm HERCULE de l'A.M.AS.
2. La surface d'un cercle est donnée par la formule :
S = π . r2 où r est le rayon du cercle, c'est à dire la moitié de son diamètre.
Calculez de combien de fois est augmenté l'éclat d'une étoile vue dans le télescope de 400mm, en considérant que la pupille de l'œil (son diamètre optique en quelque sorte) a un diamètre maximal de 6mm.
Solution :
La pupille de l'œil a un rayon de 3mm donc sa surface vaut :
Sœil = π.32 = 3,14 . 9 = 28,3mm2
La surface du miroir principal de 400mm de diamètre (donc 200mm de rayon) vaut :
Stel = π.2002 = 3,14 . 40 000 = 125 600mm2
Appelons R le rapport de ces deux surfaces :
Cela signifie que la surface du miroir est 4438 fois plus grande que la pupille de l'œil. Il entre donc 4438 fois plus de lumière dans cet instrument que dans l'œil nu. Ainsi en observant à travers ce télescope nous voyons les étoiles 4438 fois plus lumineuses ou si vous préférez nous percevons avec cet instrument des étoiles 4438 fois plus faibles que les plus faibles étoiles visibles à l'œil nu.
NB : Ce résultat est très approximatif car nous avons négligé plusieurs aspects (occultation par le miroir plan, facteur de réflexion, grossissement, ...)
3. Calculez la longueur de la diagonale d'un carré qui a un centimètre de côté (ici il s'agit bien de la figure géométrique).
Solution :
Dessinons quatre carrés de un centimètre de coté et juxtaposons-les comme sur la figure ci-contre. Nous avons aussi tracé une diagonale pour chacun de ceux-ci de façon à former un nouveau carré dont chaque côté vaut la diagonale des premiers carrés.
Ce nouveau carré est constitué par les quatre triangles A,B,C et D. Or chacun de ces triangles a une surface qui vaut la moitié de celle de nos premiers carrés. Donc le carré formé par les diagonales a une surface double de celle des petits carrés, soit 2 cm².
Notre problème consiste donc à déterminer la valeur d'un côté de ce nouveau carré.
Nous savons que la surface d'un carré vaut le carré de la valeur de son côté.
S = a² a est le côté du carré et S sa surface.
On peut dire aussi que le côté d'un carré est égal à la racine carrée de sa surface.
ceci est équivalent à la formule précédente.
Or ici S = 2cm²
donc 
Ainsi nous pouvons dire que la diagonale d'un carré est égale à son côté multiplié par racine carrée de deux.
4. Calculez le volume d'une sphère de 3m de diamètre à partir de la formule suivante :
D est le diamètre de la sphère
Solution :
5. Sachant qu'une année-lumière est la distance parcourue par la lumière en une année, exprimez la valeur d'une année lumière en kilomètres avec les puissances de dix.
Dans le vide, la vitesse de la lumière (on dit aussi sa célérité) est 300 000 Km par seconde.
Solution :
Il y a 365 jours dans une année, 24 heures dans une journée, 60 minutes dans une heure et 60 secondes dans une minute. Il y a donc 365 x 24 x 60 x 60 = 31 536 000 secondes dans une année.
En une seconde la lumière parcourt 300 000 Km donc en une année elle parcourt :
31 536 000 x 300 000 = 9 460 800 000 000 Km
Ce résultat s'exprime mieux avec les puissances de dix :
1 année-lumière = 9,4.1012Km
Ou, si vous préférez, une année-lumière vaut 9,4 millions de millions de kilomètres ou 9,4 billions de kilomètres.
Remarque : l'unité billion existe aussi en langue anglaise mais elle y a une définition différente. Ceci provoque habituellement des erreurs de traduction. En français, un billion vaut un million de millions alors que pour un anglais il vaut seulement mille millions (pour nous cela correspond à un milliard).
6. Connaissant le prix HT (Hors Taxe) et le taux de la TVA (Taxe à la Valeur Ajoutée), comment doit on faire pour calculer le prix TTC et inversement, connaissant le prix TTC, comment calcule-t-on le prix HT?
Nous considérons un objet qui coûte 80€ HT et le taux de la TVA est égal à 19,6%.
Solution :
Prix TTC = Prix HT + TVA
Pour calculer le prix TTC il faut ajouter les 19,6% de TVA aux 100% du prix HT. Autrement dit :
Prix TTC = (100% + 19,6%) x Prix HT
Ceci est équivalent à :
Prix TTC = 119,6% x Prix HT
Un pourcentage est un rapport à 100, on peut donc écrire :
119,6% = 119,6 / 100 = 1,196
et donc :
Prix TTC = Prix HT x 1,196
Ces considérations nous ont permis de remplacer la formule de la règle de 3 par une simple multiplication. Dans notre exemple, nous obtenons :
Prix TTC = 80 x 1,196 = 95,68€
Traitons maintenant du cas inverse. Nous connaissons le prix TTC = 95,68€ et nous voulons calculer le prix HT. Pour ce calcul, nous prenons l'opération inverse de la multiplication, c'est la division :
Prix HT = Prix TTC / 1,196 "Le Prix HT est égal au prix TTC divisé par 1,196"
Appliquons cette formule :
Prix HT = 96,68 / 1,196 = 80€
Nous retrouvons donc les 80€ HT que nous avions au début.
Association Marseillaise d'AStronomie
© Serge BERTORELLO : Tous les documents présents sur ce site sont protégés par les lois sur les droits d'auteur.
La reproduction et la diffusion de ces documents sont interdites sans le consentement de l'auteur.
