Lois de Kepler et principes de Newton
Oh ! Comme il est étrange d'apprendre ! La connaissance s'accroche à l'esprit dès qu'elle l'a touché, comme le lichen sur le rocher. (" Frankenstein " par Mary Shelley)
L'histoire de l'interprétation du mouvement des planètes a été marquée par des personnages extraordinaires qui ont fait progresser à pas de géant notre conscience de l'Univers. Notamment, les connaissances que nous ont transmises Kepler et Newton ont montré le chemin à la pensée humaine pour sortir de la gangue des superstitions et des croyances.
Nous allons montrer ici, par des démonstrations élémentaires, comment Newton a retrouvé les trois lois de Kepler à partir des principes fondamentaux qu'il a énoncés.
Nous commencerons par un rappel sur deux notions de géométrie ainsi que sur le contexte historique de ces deux personnages.
Notions de géométrie
Aujourd’hui la mécanique céleste est, par excellence, LE domaine d’application de l’algèbre et il serait difficile de présenter un exposé de mécanique céleste sans faire un grand étalage d’équations mathématiques. Mais, aux temps de Kepler et Newton, les démonstrations dans ce domaine se faisaient souvent avec la géométrie.
La géométrie est la partie des mathématiques qui étudie les relations entre points, droites, courbes, surfaces et volumes de l'espace. Les démonstrations géométriques consistent souvent en des comparaisons de longueurs ou d'angles.
Les deux notions très simples que nous allons examiner devraient être connues de tout astronome amateur.
Une ellipse est une conique, on peut l'obtenir par l'intersection entre un cône de révolution et un plan orienté entre la génératrice du cône et la perpendiculaire à son axe de symétrie.
Pour tracer cette figure sur une feuille de papier, je vous propose une méthode avec deux clous (ou deux punaises) et une ficelle comme illustré sur la figure 1.
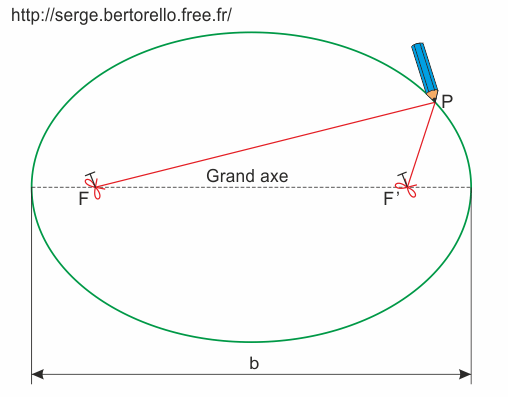
F et F' sont les foyers de l'ellipse.
Longueur de la ficelle (sans les nœuds) = longueur du grand axe.
Selon cette procédure, on plante les deux clous sur des points que l'on nomme foyers et on les relie par une ficelle plus longue que la distance qui les sépare. On trace l'ellipse en faisant glisser le crayon tout en tendant soigneusement le fil avec sa pointe.
Nous constatons alors une propriété fondamentale de l'ellipse : la somme des distances entre chaque foyer et le crayon est constante. Ainsi, pour chaque point "P" de l'ellipse, si on ajoute la distance entre ce point et un foyer (FP) à la distance entre ce point et l'autre foyer (F'P), on obtient une longueur constante. Le résultat de cette addition est le même pour tous les points de cette figure, il est égal à la longueur de la ficelle ainsi qu'à la longueur du grand axe "b" de l'ellipse.
Nous pouvons aussi exprimer cette idée avec l'équation suivante :
- b = FP + F'P [1]

L'aire "a" d'un triangle est égale à la moitié du produit de sa base "b" par sa hauteur "h" :
 [2]
[2]Pour ce calcul, on choisit un côté quelconque du triangle dont on considère qu'il est la base. Pour la figure 2, nous avons choisi le côté AC.
Ensuite, on détermine sa hauteur. La hauteur du triangle est la distance qui sépare la base du sommet qui lui est opposé, la hauteur est mesurée perpendiculairement à la base. Le segment de droite sur lequel on mesure cette hauteur peut être, selon le cas, à l'intérieur ou à l'extérieur du triangle.
Notez bien que, si nous avions pris pour base un autre côté du triangle tout en considérant la hauteur correspondante, le résultat du calcul de son aire aurait été le même.
Ainsi, différents triangles qui ont une base et une hauteur semblables auront la même aire. Tous les triangles de la figure 3 ont la même aire.

L'animation suivante illustre aussi cette idée.

Nous en savons maintenant assez pour suivre les traces des génies. Voyons tout d'abord le contexte dans lequel est arrivé Kepler.
Avant Kepler
Johannes Kepler est né le 27 décembre 1571 près de Stuttgart (Allemagne) en pleine période de la renaissance et il est mort le 15 novembre 1630 à Ratisbonne en Bavière.
Au moment de sa naissance, les personnes instruites discernaient mal ce qui appartenait au domaine des croyances de ce qui était du champ des connaissances. Pour le sujet qui nous intéresse ici, nous pouvons dire qu'il y avait une grande confusion entre astrologie et astronomie. Pour définir la trajectoire de la Lune, du Soleil et des planètes sur la voûte étoilée on se référait à Aristote et à Ptolémée. De plus, il était dangereux de contredire les quelques rares remarques astronomiques des "saintes écritures".
Conseil de lecture : "L'homme et le cosmos" par Stéphane GROUEFF.
Aristote
Aristote était un philosophe grec né en 384 avant JC et mort en 322 avant JC. Il avait une vision géocentrique de l'Univers. Il considérait que la Terre est fixe au centre de l'univers et que tous les astres tournent autour d'elle selon des trajectoires circulaires.
Cette idée permettait d'expliquer grossièrement les mouvements apparents de la Lune et du Soleil qui sont à peu près réguliers mais elle ne pouvait pas justifier la complexité du mouvement des planètes qui parcourent la voûte céleste en effectuant des boucles comme le montre la figure 5.

Carte obtenue avec le logiciel Skyglobe pour Windows.
Nous voyons la planète Mars se déplacer vers l'Est à travers les constellations puis elle ralentit pour ensuite rétrograder vers l'Ouest avant de repartir à nouveau en direction de l'orient. On constate aussi ce type de trajectoire pour les autres planètes.

La Terre est au centre et le Soleil tourne autour d'elle sur la 4ième sphère.
Pour les planètes Mercure et Vénus, ces boucles se forment autour de la position du Soleil dont elles ne s'éloignent jamais au-delà d'une limite propre à chacune d'elles.
La théorie d'Aristote n'explique pas ces parcours avec des retours en arrière. En effet, si toutes les planètes tournaient sur des cercles centrés sur la Terre, nous les verrions progresser toujours dans le même sens.
Cette hypothèse n'expliquait pas non plus les grandes variations de l'éclat lumineux des planètes, elle ne disait rien sur ce sujet.
Ptolémée
Pour rendre compte de ces aspects, Ptolémée a proposé une modification au modèle d'Aristote.

La trajectoire résultante de la planète est tracée en bleu.
Claude Ptolémée, communément appelé Ptolémée, était un astronome (et astrologue), probablement d'origine grecque, qui vivait à Alexandrie en Egypte au 2ième siècle. Il a conservé la position centrale et fixe de la Terre mais chaque planète tournait cette fois autour d'un point qui suit la trajectoire circulaire d'Aristote.
Ainsi chaque planète effectuait un petit cercle nommé épicycle dont le centre se déplaçait sur le déférent.
Cette disposition décrivait mieux les trajets des planètes et elle expliquait aussi les variations d'éclats par des variations de distances.
Pour Mercure et Vénus, il fallait compléter ce modèle en imposant à leur épicycle de rester sur la ligne qui relie la Terre au Soleil afin d'expliquer que ces planètes ne s'éloignent jamais du Soleil.
Le système de Ptolémée réussissait à décrire les rétrogradations des planètes et les variations de leurs éclats mais il n'expliquait pas d'autres irrégularités du mouvement des planètes. Pour améliorer la fidélité de son modèle, Ptolémée a ensuite considéré des excentriques, les cercles qui le composaient ne tournaient plus autour de leur centre mais autour d'un point voisin (excentrique)... Ce modèle devenait de plus en plus complexe sans jamais être complètement satisfaisant.
Copernic
Nicolas Copernic était un chanoine, médecin et astronome polonais né à Thorn en 1473 et mort à Frauenburg en 1543.

Copernic était conscient des insuffisances du système de Ptolémée et il l'a reconsidéré en mettant le Soleil au centre de l'Univers. Selon cette représentation, la rétrogradation est provoquée par la simple combinaison des déplacements de la Terre et de la planète considérée.
Il n'était certainement pas le premier à y avoir pensé mais, à cette époque on craignait la censure (et la répression) des autorités religieuses. Or l'idée de chasser la Terre (et l'homme) du centre de l'Univers était mal perçue par la communauté religieuse. Pour énoncer sans danger une telle théorie, il fallait donc avoir, comme Copernic, des solides appuis auprès de relations religieuses et politiques hautement placées, en plus de sérieuses compétences en astronomie.
Copernic a exposé son système planétaire dans son ouvrage "De Revolutionibus Orbium Coelestium" qui a été imprimé juste avant sa mort en 1543. Dans celui-ci, il indique que les planètes, y compris la Terre, tournent autour du Soleil en suivant des trajectoires parfaitement circulaires et toutes dans le même sens. Chacune d'elles évolue dans un plan différent qui est peu incliné par rapport au plan de l'orbite de la Terre (plan de l'écliptique).
Cet astronome a consacré beaucoup de temps et d'énergie au perfectionnement de sa théorie. Il a étudié une compilation d'observations remontant jusqu'à l'antiquité et il a lui-même arpenté inlassablement le ciel.

On n'a pas compris tout de suite que le système de Copernic constituait une avancée très importante pour la pensée humaine. Toutefois, hormis la rétrogradation, il n'explique pas mieux les irrégularités de la marche des planètes dans le ciel. Ceci fut une des causes de la parution très tardive de son livre qui a été un étonnant échec de librairie.
Finalement, pour que son modèle décrive mieux le comportement des planètes, Copernic a lui-aussi fait appel à des épicycles et des excentriques. Ainsi, malgré les apparences, ce système révolutionnaire n'est pas beaucoup plus simple que celui de Ptolémée.
Le système de Copernic ne s'est donc pas imposé aux esprits critiques de l'époque car il n'était pas assez convainquant.
Conseil de lecture : Jean-Pierre Luminet a écrit une biographie romancée de cet astronome intitulée "Le secret de Copernic".
Tycho Brahé
Tycho Brahé était un astronome Danois né à Knudstrup en 1546 et mort à Prague en 1601.

Quand on évoque ce truculent personnage du pays de Hamlet, on rappelle souvent qu'il a perdu un bout de son nez dans un duel, ce qui l'a ensuite condamné à porter un nez postiche.
Il s'est spécialisé dans la mesure de position des étoiles et des planètes. Il était très talentueux pour cela et il a disposé des meilleurs instruments qu'il était possible de fabriquer avant l'invention de la lunette astronomique.
La renommée de Tycho Brahé a commencé à s'imposer à l'occasion de l'apparition d'une étoile nouvelle dans la constellation de Cassiopée en novembre 1572. Ses observations ont montré avec une grande précision que le nouvel astre était immobile par rapport aux étoiles voisines prouvant ainsi qu'il s'agissait bien d'une étoile et non d'une planète. Au cours de l'année suivante, il a publié ces observations avec une description de ses propres instruments dans un livre intitulé "De Nova Stella".
Ce changement sur la voûte stellaire contredisait les enseignements d'Aristote qui affirmait que tout changement (ou "corruption") ne pouvait survenir qu'à proximité immédiate de la Terre. Celui-ci affirmait notamment que les comètes étaient des phénomènes sublunaires voire même atmosphériques. Le reste de l'Univers devait être immuable depuis sa création. Le sujet était donc délicat et c'est pour cela que Tycho Brahé a soigneusement expliqué ses méthodes.

Quelques années plus tard, un autre astre lui a encore permis de contredire Aristote. En effet, ses observations de la grande comète de 1577 ont prouvé que celle-ci voyageait à une distance au moins six fois plus grande que celle de la Lune.
De 1576 à 1597, Tycho Brahé s'est vu confié la direction de l'observatoire Uraniborg situé sur l'ile de Hveen.
Il était opposé aux thèses héliocentriques de Copernic et préférait considérer la Terre fixe au centre de l'Univers. En fait, il croyait que les planètes tournaient autour du Soleil et que celui-ci tournait autour de nous avec tout ce cortège. C'était une sorte de compromis entre le système d'Aristote et celui de Copernic.
C'est dans le but de prouver la supériorité de sa théorie sur celle de Copernic qu'il a effectué depuis Uraniborg un grand nombre de mesures de positions des planètes qu'il a soigneusement consignées par écrit. Cependant, Tycho Brahé était un observateur et il avait besoin d'un mathématicien pour exploiter ses mesures. Ceci le conduisit à rechercher la participation de Kepler.
C'est en 1600, que l'astronome et mathématicien Kepler rencontra Brahé et devint son collaborateur.
Quelques mois plus tard, la mort emporta Tycho Brahé et Kepler récupéra une partie de ses observations.
Conseils de lecture :
"Tycho Brahé l'homme au nez d'or", c'est une biographie romancée de Tycho Brahé par Henriette Chardak.
"L’île aux étoiles de Tycho", Biographie de Tycho Brahé, c'est un épisode de la série "À la mesure du ciel" de l'IMCCE.
Les lois de Kepler

Pendant les années qui ont suivi, l'astronome allemand Johannes Kepler (1571 - 1630) a alors étudié les mesures de Tycho Brahé dans le but de comprendre les mouvements des planètes.
Soyons bien conscients qu'à ce moment-là personne ne savait prédire la position de ces astres errants avec une précision convaincante.
Dans ses analyses, Kepler s'appuyait sur l'hypothèse héliocentrique (Soleil au centre du système) mais, comme ses contemporains, il a tout d'abord voulu faire coïncider les trajectoires des planètes avec des cercles éventuellement excentrés. Ce n'était pas possible.
Finalement, c'est de l'étude des positions de la planète Mars que la solution a commencé à germer dans l'esprit de Kepler.
En 1609, Kepler publia un livre intitulé "Astronomia nova" (Astronomie nouvelle) dans lequel il exposait les deux premières lois que l'histoire des sciences a attachées à son nom.
Neuf années plus tard, en 1618, il énonça sa troisième loi.
Conseil de lecture : "Kepler le chien des étoiles", c'est une biographie romancée de Johannes Kepler par Henriette Chardak.
Film recommandé : "L'œil de l'astronome" réalisé par Stan Neumann en 2012. Ce film nous présente la confrontation de Képler et de ses théories face aux réticences de ses contemporains.

Voilà ce qui manquait au système de Copernic pour être probant.
Jusqu'à l'énoncé de cette loi, l'intelligence des astronomes s'est perdue dans la croyance que les astres suivent des trajectoires circulaires. Grâce à cette première loi de Kepler, il n'est plus besoin de prendre en considération les épicycles, excentriques et autres complications des systèmes précédents.

Cette loi indique comment varie la vitesse de déplacement des planètes tout au long de leur révolution.
Ce que Kepler appelle "rayon vecteur" est la ligne imaginaire qui relie le centre de la planète considérée au centre du Soleil.
Considérons différentes portions de l'orbite parcourues par une planète pendant des durées égales. La deuxième loi de Kepler nous indique que la surface décrite par le rayon vecteur est la même pour chacune de ces portions.
Ceci signifie aussi que les planètes avancent plus vite quand elles sont proches du Soleil et plus lentement quand elles sont éloignées.
Aujourd’hui, nous dirions :
Les carrés des périodes de révolution des planètes sont proportionnels aux cubes des grands axes de leurs orbites.
Nous pouvons aussi énoncer cette règle avec l'expression suivante :
 [3]
[3]
avec : a = demi-grand axe de l'orbite
T = période de révolution
k = constante
Cette loi relie entre-elles toutes les planètes du système solaire. Elle explique que la durée de révolution autour du Soleil est d'autant plus longue que l'orbite de la planète est éloignée de l'étoile centrale.
Bien que Kepler ait beaucoup travaillé sur la nature des forces qui régissent le mouvement des planètes, il faut constater que ses trois fameuses lois n'expliquent rien. Elles se contentent de décrire les trajectoires planétaires.
Et encore, il faut être conscient que ces lois ne décrivent pas tous les mouvements du système solaire comme par exemple :
- Certaines comètes suivent des orbites qui n'obéissent pas à ces lois.
- Kepler ne dit rien sur les mouvements de précession comme ceux de la Terre et de la Lune.
Toutefois, sans le savoir, Kepler préparait le terrain pour Newton.
Isaac Newton
Selon notre calendrier grégorien, Isaac Newton est né le 6 janvier 1643 à Woolsthorpe en Angleterre dans le Lincolnshire et il est mort le 31 mars 1727 à Londres. A cette époque, les anglais employaient encore le calendrier julien et leurs dates étaient donc décalées d'une dizaine de jours par rapport aux nôtres. C'est pour cela que certains auteurs ont affirmé que Newton est né pendant l'année de la disparition de Galilée (1642). En fait, ils ont fait une confusion entre les deux calendriers.
Galileo Galilei dit Galilée est né à Pise le 15 février 1564 et mort à Arcetri près de Florence le 8 janvier 1642.
Isaac Newton s'est illustré dans un grand nombre de disciplines. Pour ce qui nous intéresse ici, il a notamment fait preuve de génie en mathématiques, physique et astronomie.
En 1687, il a publié un ouvrage d'une importance capitale dans l'histoire des sciences. Il l'a écrit en latin et intitulé "Philosophiae naturalis principia mathematica", ce qu'on peut traduire par "Principes mathématiques de la philosophie naturelle".

Dans ce livre, Newton a énoncé des principes qui constituent le fondement de la mécanique classique et de la loi de la gravitation universelle.
Les lois de Kepler étaient déduites des observations. Les lois de Newton sont d’une nature radicalement différente. Elles sont des hypothèses sur la réalité physique des relations entre matière, forces et mouvements. Nous allons les énoncer en vérifiant leur compatibilité avec celles de Kepler.
Cette loi inspirée par les travaux de Galilée est en opposition avec les idées d’Aristote qui pensait qu’un objet est forcément immobile si aucune force n’agit sur lui. Elle constitue la base de ce qu'on nomme aujourd'hui le "Principe d'Inertie".
La figure suivante illustre le déplacement rectiligne uniforme d'une planète hypothétique éloignée de toute force extérieure. Elle se déplace en ligne droite avec une vitesse uniforme.

Imaginons maintenant, comme Kepler l'avait fait pour les planètes autour du Soleil, le rayon vecteur qui relie ce corps à un point P que nous choisissons arbitrairement dans l'espace environnant. Ensuite, nous considérons plusieurs tronçons quelconques de la trajectoire du mobile parcourus avec la même durée.

Des aires parcourues par ces rayons vecteurs au cours de ces tronçons sont illustrées ci-après.

Ces aires sont des triangles qui ont la même hauteur et des bases de même valeur puisque celles-ci ont été parcourues pendant des durées identiques et avec la même vitesse. Comme nous l'avons vu précédemment, cela signifie que ces triangles parcourus pendant des durées égales ont la même aire.
Nous pouvons conclure que, en l'absence de force extérieure, le premier principe de Newton permet de trouver une propriété qui ressemble à la deuxième loi de Kepler. Nous utiliserons ce résultat plus loin.
Aujourd'hui, on considère que c'est le principe fondamental de la dynamique.
Les actions mutuelles de deux corps l’un sur l’autre sont toujours égales et dirigées en sens contraires.
C'est la loi qui exprime la réciprocité entre l'action et la réaction. Dans le contexte qui nous intéresse ici, elle indique que les planètes exercent sur le Soleil des forces égales et opposées aux forces que leur applique le Soleil.
C'est aussi avec ce principe que l'on démontre qu'un objet sphérique et homogène (planète ou Soleil) peut être considéré comme un simple point dans les calculs de trajectoire.
Nous n'utiliserons pas cette loi de façon explicite dans les raisonnements qui suivent mais c'est elle qui nous permet de simplifier notre étude en considérant Soleil et planètes comme des points sans dimension.
Principes de Newton et loi des aires
Selon le premier principe de Newton, une planète a tendance à se déplacer en ligne droite et avec une vitesse constante si aucune force n'agit sur elle. Selon le second principe, elle va acquérir un mouvement sous l'action de la force gravitationnelle du Soleil. Newton considère donc que la trajectoire d'une planète résulte de l'action de ces deux effets.
Newton nous propose d'étudier ce mouvement sur les figures suivantes dans lesquelles la lettre "S" désigne le Soleil et les lettres A,B,C,D indiquent des positions successives de la planète considérée à des intervalles de temps égaux et très petits.
Sur la figure suivante, nous considérons une planète au point A. Sous l'effet de son mouvement, le premier principe de Newton nous indique qu'elle va suivre un déplacement rectiligne avec une vitesse constante pour se rendre au point B après un petit intervalle de temps.
En fait, comme elle est attirée par le Soleil, elle acquiert pendant ce temps un mouvement dirigé vers cet astre. La vitesse de cette nouvelle composante du déplacement de la planète est figurée par la flèche rouge.

Après un deuxième intervalle de temps (égal au premier) et selon le premier principe, la planète devrait avoir parcouru la même distance dans la même direction si elle ne subissait pas la force du Soleil et elle arriverait au point "c" (figure 20).
Toutefois, la vitesse qu'elle a acquise en direction du Soleil incurve sa trajectoire et elle arrive au point "C" dont nous allons maintenant définir la position.
La vitesse en direction du Soleil acquise pendant le premier intervalle de temps provoque dans l'intervalle suivant un déplacement vers l'étoile centrale représenté par le segment Bv orienté lui-aussi vers le Soleil. Il nous faut donc reporter cette longueur à partir du point "c" pour obtenir le point "C". Ainsi, le segment cC est de même longueur et de même orientation que le segment Bv (cC est parallèle à Bv).
Remarquons que la figure définie par les points BvCc est un parallélogramme dont la planète parcourt la diagonale BC.

Et ainsi de suite, on va pouvoir figurer les intervalles suivants (figure 21).
Nous obtenons ainsi une trajectoire "brisée" alors que nous savons bien que la trajectoire réelle est lisse. Il ne faut pas oublier que les segments de droite que nous avons tracés ne servent qu'à supporter le raisonnement. Cela signifie que nous devons considérer que nos intervalles de temps sont "infiniment petits" pour retrouver l'aspect lisse du cheminement de la planète.

Considérons maintenant les aires décrites par les rayons vecteurs pendant deux intervalles de temps consécutifs.
Sur la figure 22, nous avons coloré les deux aires qui auraient été décrites en l'absence de la force d'attraction du Soleil. Seul le premier principe de Newton intervient ici et nous avons démontré plus haut que ces aires sont égales car les deux triangles (bleu et vert) ont la même hauteur et leurs bases AB et Bc sont de même longueur.
L'aire du triangle ABS est égale à celle du triangle BcS.

Or dans le cas présent, la force d'attraction du Soleil a infléchi la trajectoire de la planète et l'aire décrite pendant le second intervalle de temps est donc celle du triangle BCS qui est colorée en rose sur la figure 23.

Comme nous l'avons indiqué plus haut, le segment Cc est parallèle au segment Bv. Cela signifie que les triangles BcS et BCS ont la même hauteur "h" si on considère que leur base est BS.

Ils ont la même base et la même hauteur, cela signifie que les triangles BcS et BCS ont la même aire.
Nous avons vu précédemment que les aires des triangles ABS et BcS sont égales, nous pouvons donc déduire que les aires de ABS et BCS sont aussi égales.
Conclusion : pendant des intervalles de temps égaux, le rayon vecteur de la planète décrit des aires égales. C'est une façon d'exprimer la deuxième loi de Kepler.
Nous venons donc de retrouver la deuxième loi de Kepler à partir des principes de Newton et, pour cela, nous nous sommes initiés au calcul infinitésimal en décomposant par la pensée une trajectoire continue en petits segments de droites.
Nous voyons sur la figure 24 la page du livre "Philosophiae naturalis principia mathematica" qui présente l'illustration que Newton a employée pour présenter le raisonnement que nous venons de suivre. Avec cette démonstration, il a été l'initiateur du calcul infinitésimal, une méthode qui a pris par la suite une importance majeure en physique.
Variation de la force d'attraction gravitationnelle avec la distance
Les principes de Newton n'indiquent rien sur le lien qu'il peut y avoir entre la valeur de la force d'attraction gravitationnelle qui attire deux astres et la distance qui les sépare. Nous devrons faire appel aux lois de Kepler.
Pour établir notre raisonnement, nous allons considérer une planète hypothétique qui possède une orbite circulaire (le cercle est une ellipse dont l'excentricité est nulle) et nous allons construire son diagramme des vitesses.
Notons tout d'abord que la deuxième loi de Kepler nous indique que la vitesse de déplacement de cette planète est constante puisque sa distance au Soleil ne varie pas.
A gauche de la figure suivante, nous avons illustré la planète en deux positions successives séparées par un petit intervalle de temps. La flèche tout d'abord noire puis orange représente la vitesse de cet astre. Sa longueur est constante (vitesse constante) mais son orientation évolue tout au long de l'orbite.
Pour construire le diagramme des vitesses, nous récupérons ces flèches en leur donnant la même origine.

Si nous considérons l'évolution sur l'ensemble de l'orbite, nous constatons que la flèche du diagramme des vitesses décrit elle-aussi un cercle. Cette flèche tourne à la même vitesse que la planète mais elle est décalée de 90° puisque dans le cas d'une orbite circulaire le déplacement est toujours perpendiculaire au rayon vecteur.
Le parcours de son orbite par la planète est appelé "révolution" et la durée "T" de ce parcours est la "période de révolution".
Le rayon du cercle des vitesses est égal à la vitesse "v" de la planète (figure 26).

Calculons cette vitesse de déplacement de la planète sur son orbite en nous inspirant de l'image de gauche :
 [4]
[4]De la même façon, nous calculons la variation de la vitesse "Vv" ou, si vous préférez, la vitesse de déplacement du vecteur vitesse sur son diagramme qui est un cercle de rayon "v" parcouru par le vecteur pendant le temps "T" (image de droite), en n'oubliant pas que le deuxième principe de Newton indique que la variation de la vitesse est proportionnelle à la force appliquée :
 [5]
[5]
Le signe "~" signifie "est proportionnel à".
Remplaçons dans cette équation la vitesse "v" par son expression dans l'équation [4] :
 [6]
[6]Simplifions en nous concentrant sur F :
 [7]
[7]Eliminons l'expression constante (2π)2 :
 [8]
[8]Faisons maintenant appel à la troisième loi de Kepler avec la notation que nous avons ici. Nous pouvons l'exprimer en disant que T2 est proportionnel à R3. Remplaçons donc T2 par R3 dans l'équation [8] et nous obtenons :
 [9]
[9]Il ne nous reste plus qu'à simplifier cette fraction en divisant son numérateur et son dénominateur par R :
 [10]
[10]Conclusion : La force gravitationnelle avec laquelle le Soleil et les planètes s'attirent diminue avec le carré de la distance.
Forme des orbites planétaires
Pour analyser la forme de ces orbites, nous allons maintenant construire un nouveau diagramme des vitesses à partir duquel nous reconstruirons la forme de l'orbite. Cela nous permettra d'identifier ses propriétés et d'en déduire sa forme.
Observons la figure 27 en nous rappelant la deuxième loi de Kepler que nous avons retrouvée plus haut à partir des principes de Newton. Les deux zones colorées en bleu ont la même aire, elles ont été générées par des rayons vecteurs en des temps égaux.

Considérons maintenant des angles de parcours orbital égaux sur la figure 28.

La loi des aires nous indique que les temps de parcours correspondants aux deux zones bleutées sont proportionnels à leurs aires.
Par ailleurs, nous savons que l'aire d'une surface est proportionnelle au carré de ses dimensions.
Par conséquent, si nous divisons une orbite en angles de parcours égaux, le temps "t" mis par la planète pour parcourir un de ces angles est proportionnel au carré de la distance au soleil "R" :
- t ~ R2 [11]
Nous avons appris au chapitre précédent :
 [10]
[10]Le deuxième principe de Newton nous indique que la variation de vitesse "Vv" de la planète est proportionnelle à la force "F" qu'elle reçoit du Soleil. Elle est aussi proportionnelle à la durée "t" d'application de cette force :
- Vv ~ F.t [12]
Remplaçons "F" et "t" par les grandeurs proportionnelles indiquées par les relations [10] et [11] :
 [13]
[13]Cela signifie que, pour des angles de parcours orbital égaux, la variation de vitesse ne dépend pas de R, elle est constante.
Par conséquent, si nous divisons notre orbite en un certain nombre d'angles de parcours orbital égaux, le diagramme des vitesses correspondant sera un polygone avec autant de segments égaux qui correspondront à des variations de vitesse égales (c'est un polygone régulier).
Exemple : divisons l'orbite en 12 angles égaux, c'est à dire en 12 angles de 30° (en effet, 12x30=360) et construisons le diagramme des vitesses.

La partie gauche de la figure 29 montre l'orbite de la planète divisée en douze angles de 30° ainsi que le vecteur vitesse de la planète. Ce dernier est illustré par une flèche qui indique la direction de déplacement au point où elle est attachée et dont la longueur est proportionnelle à la vitesse. Nous récupérons ce vecteur vitesse dans la partie de droite pour commencer la construction du diagramme des vitesses.
Nous avons décidé arbitrairement de commencer cette construction à partir du point où la planète est le plus proche du Soleil et où sa vitesse est la plus grande, ce point se nomme "le périhélie".
Considérons maintenant le point suivant sur l'orbite, la ligne qui le relie au Soleil forme un angle de 30° avec la ligne qui relie le précédent (figure 30).

Rapportons le vecteur vitesse sur le diagramme en l'attachant au point origine des vitesses "O".
Le segment de droite "Vv" qui relie les extrémités des deux vecteurs vitesse représente la "Variation de vitesse" et avons démontré qu'il est un côté d'un polygone régulier à 12 faces. Il correspond donc à un angle de 30° dont le sommet est au centre "C" de ce polygone.
La figure 31 représente la construction du point suivant.

Et ainsi de suite... La figure 32 montre la construction complète de ce diagramme des vitesses des 12 points espacés de 30° que nous avons sélectionnés sur l'orbite de la planète.

Si nous avions divisé l'orbite en un nombre infiniment grand de secteurs conformément à la réalité, le diagramme des vitesses aurait été un cercle.
Remarquons que l'origine des vitesses n'est pas au centre de ce cercle.
Maintenant, nous allons effectuer la démarche inverse. A partir du diagramme circulaire des vitesses avec une origine des vitesses excentrée, nous allons reconstruire la forme de l'orbite.
La figure 33 illustre le début de cette procédure.

Dans le but de simplifier notre démarche, nous allons faire pivoter de 90° le diagramme des vitesses (figure 34).

Nous allons maintenant reconstruire la forme de l'orbite dans le diagramme des vitesses ainsi orienté.
Commençons par reconstruire le point P' qui correspond au point P de l'orbite (figure 35). Pour cela, nous allons considérer la médiatrice du vecteur vitesse dans le diagramme des vitesses. Grâce au pivotement, la médiatrice du vecteur vitesse est maintenant parallèle au vecteur vitesse de l'image de gauche.

Le point P' est situé à l'intersection de la médiatrice du vecteur vitesse et du rayon qui fait un angle θ avec le rayon origine. Voici pour un premier point.
Pour construire un autre point dont le rayon vecteur fait un angle γ avec la direction du périhélie, nous commençons par tracer un rayon du diagramme des vitesses qui forme un angle γ avec l'origine. Son intersection avec le cercle nous donne la position de l'extrémité de la flèche du vecteur vitesse. La médiatrice de ce vecteur coupe le nouveau rayon au point M', c'est notre deuxième point de la courbe.
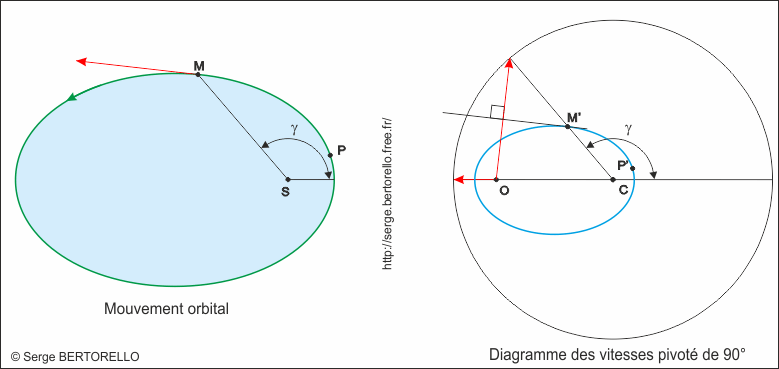
Et ainsi de suite, nous construisons une courbe à l'intérieur du diagramme des vitesses qui serait exactement superposable à la trajectoire de la planète si nous la tracions à la même échelle.
Notre problème actuel revient donc à déterminer la forme de cette dernière courbe.
Pour cela, nous allons considérer un point quelconque de cette trajectoire reconstruite, appelons-le "N" sur la figure 37.

Pour construire ce point, nous avons considéré le rayon quelconque Cb puis nous avons tracé le segment Ob qui correspond au vecteur vitesse. Enfin, la médiatrice de ce segment coupe le rayon Cb en N qui appartient à la courbe étudiée. Notre figure est terminée.
Considérons maintenant les deux triangles que nous avons colorés, l'un en rose et l'autre en bleu (OaN et baN). Le segment aN est un côté commun aux deux triangles. Par ailleurs, le point "a" est situé au milieu de Ob et les deux triangles ont en ce point un angle droit (par définition de la médiatrice).
Ces deux triangles ont donc deux côtés et un angle égaux. Ils sont donc superposables (en pliant la figure selon la médiatrice aN) et leurs troisièmes côtés sont donc aussi égaux :
- ON = bN [14]
La relation ente bN et le rayon R est évidente :
- R = bC = bN + NC [15]
L'égalité [14] nous permet de remplacer bN par ON, nous obtenons :
- R = ON + NC [16]
Comme la longueur du rayon R est constante, le point N est sur une courbe pour laquelle la somme des segments ON et Nc est constante. Ceci définit une ellipse comme nous l'avons rappelé plus haut (rappel sur l'ellipse). Notons aussi que dans notre construction, le point C correspond à la position du Soleil. Celui-ci occupe donc un foyer de l'ellipse.
Ainsi, nous venons de démontrer la première loi de Kepler.
Je dois indiquer que je me suis inspiré d'un cours de Richard Feynman (physicien américain 1918 - 1988) pour développer cette dernière démonstration. Newton a employé une démarche différente.
Conseil de lecture : "Philosophiae naturalis principia mathematica" par Isaac Newton, voici deux sites où vous pouvez le consulter :
- UQAC - Université du Québec à Chicoutimi
- Cambridge Digital Library
La loi de la gravitation universelle
Universalité
Dans les démonstrations précédentes, nous sommes restés au niveau des conceptions élémentaires telles que les a présentées Newton dans son ouvrage "Philosophiae Naturalis Principia Mathematica". Certains aspects de celles-ci peuvent paraître naïfs aujourd'hui.
Ces principes de Newton sont à la base de ce que nous appelons aujourd'hui la "loi de la gravitation universelle" qui s'exprime de la façon suivante :
Notez bien qu'il s'agit d'une formulation moderne. Newton ne l'a jamais énoncée ainsi.
On la formule aussi avec l'égalité suivante :
 [17]
[17]
avec : F = force d'attraction gravitationnelle entre un objet de masse "m" et un autre objet de masse "M".
R = distance entre les deux objets (entre leurs centres de gravité).
G = Constante de la gravitation = 6,674 28 . 10-11 N.m2.kg-2
Le principe fondamental de la dynamique (deuxième principe de Newton) est lui-aussi décrit d'une façon différente de nos jours. On l'exprime avec la relation suivante :
 [18]
[18]
avec : F = Force appliquée sur un objet de masse "m"
γ = accélération subie par l'objet (c'est la variation de sa vitesse par unité de temps).
Une flèche est placée sur certaines grandeurs pour préciser qu'elles sont orientées
(on les qualifie alors de vectorielles).
On considère que cette loi de la gravitation est universelle car on a montré qu'elle se manifeste partout dans l'Univers. Elle explique le mouvement des galaxies lointaines, elle décrit le comportement des étoiles doubles que nous observons dans notre propre galaxie, elle nous permet de comprendre le mouvement des planètes de notre système solaire, elle justifie la chute d'une pomme sur la tête d'un génie...
Cette loi explique aussi les comportements des astres qui n'étaient pas appréhendés par Kepler. Ainsi, elle est efficace pour étudier les mouvements de précession des astres (ou d'un gyroscope), les perturbations des planètes entre-elles ou pour prédire la trajectoire non-elliptique de certaines comètes, objets qui peuvent suivre des paraboles ou des hyperboles.
Aristote prétendait que le monde terrestre corrompu sur lequel nous habitons n'est pas régi par les mêmes lois que le monde céleste où selon-lui tout est parfait... Avec la loi de la gravitation universelle, Newton a pulvérisé cette croyance.
Limites
L'énoncé des principes de Newton a bouleversé la physique. Avec eux, les astronomes ont décrit les mouvements célestes avec un grand luxe de précision. Ils ont notamment permis à Urbain Le Verrier de prédire par le calcul l'existence de la planète Neptune grâce à l'analyse de ses perturbations sur l'orbite de la planète Uranus.
Urbain Le Verrier (1811 - 1877) était un astronome français spécialiste de la mécanique céleste.
Ces lois ont permis de résoudre des problèmes qui avaient résisté depuis des millénaires à la sagacité des hommes. Les développements scientifiques à partir de cette base ont été particulièrement prolifiques en résultats spectaculaires (génie civil, architecture, balistique, astrophysique, mécanique, etc.) à un tel point qu'on n'imaginait pas que leur portée puisse être limitée d'une quelconque façon.
Avant le 20ième siècle, ces succès ont conduit de nombreux scientifiques à développer dans leur esprit des certitudes excessives. C'est ainsi qu'ils ont aveuglé certains d'entre-eux comme William THOMSON (1824 - 1907), éminent physicien plus connu sous le nom de Lord KELVIN, quand il a déclaré en 1892 :
- - Il n'y a plus rien à découvrir en physique. Il ne reste à faire que des mesures de plus en plus précises.
Il a même ajouté :
- La physique est définitivement constituée dans ses concepts fondamentaux : tout ce qu'elle peut désormais apporter, c'est la détermination précise de quelques décimales supplémentaires. Il y a bien deux petits problèmes : celui du résultat négatif de l'expérience de Michelson et celui du corps noir, mais ils seront rapidement résolus et n'altèrent en rien notre confiance.
Pourtant, les "deux petits problèmes" qu'il évoquait ont conduit à d'autres révolutions majeures telles que les théories de la relativité pour l'un et la mécanique quantique pour l'autre...
En fait, il y avait un autre problème qui avait résisté aux astronomes et notamment à Urbain Le Verrier. Quand celui-ci a voulu établir les tables du mouvement de la planète Mercure, cet habile calculateur rencontra un obstacle inattendu. Les tables qu'il a calculées avec la "physique newtonienne" ne correspondaient pas parfaitement avec les observations. Pour rétablir l'accord avec le calcul, il devait considérer que le périhélie de Mercure avance d'une quarantaine de secondes d'arc par siècle en plus de toutes les corrections nécessaires pour tenir compte des perturbations par les autres planètes.
Fort de son succès avec la découverte de Neptune et pour ne pas remettre en cause la loi de Newton, il émis l'hypothèse que cette anomalie est provoquée par une planète inconnue qui circulerait entre Mercure et le Soleil et à laquelle il donna le nom de "Vulcain".
On n'a jamais découvert une telle planète qui perturberait suffisamment Mercure pour expliquer l'avance séculaire de son périhélie. Aujourd'hui, nous sommes certains qu'elle n'existe pas.
En 1915, Albert Einstein a formulé la théorie de la relativité générale. Avec celle-ci, on montre que la loi de Newton est valable à un très haut degré d'approximation pour les planètes éloignées du Soleil mais que les effets de la gravitation n'obéissent plus à une règle aussi simple quand on s'approche de la masse imposante du Soleil.
Cette théorie de la relativité générale explique parfaitement l'avance du périhélie de Mercure.
Mais ceci est une autre histoire...
Conseils de lecture :
- "Le mouvement des planètes autour du Soleil", le cours perdu de Richard FEYNMAN.
- "L'histoire du concept de gravitation" par Sébastien CHARNOZ



