Détermination de la règle de Christiaan Huygens

Considérons un oculaire composé de deux lentilles réalisées dans le même verre. Nous allons déterminer une disposition corrigée de l'inégalité chromatique du grossissement.
Nous considérerons que les lentilles sont minces, cela signifie que nous négligerons leur épaisseur.
Distance focale de L1 = f1
Distance focale de L2 = f2
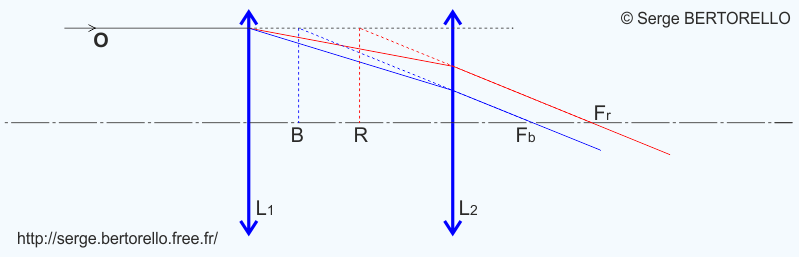
Le rayon de lumière passant par O provient du centre de l'objectif. Comme celui-ci est très éloigné en comparaison aux distances focales de nos lentilles, nous considérons que ce rayon lumineux est parallèle à l'axe optique.
Le rayon de lumière blanche incident sur la première lentille est décomposé par l'aberration chromatique et, après la sortie de la deuxième lentille les rayons sont dispersés en fonction de la longueur d'onde.
Les points Fb et Fr ne peuvent pas être confondus car les lentilles sont faites du même verre mais nous voulons que les rayons de couleurs différentes (ici bleu et rouge) sortent selon des trajets parallèles. Leur direction sera donc indépendante de la longueur d'onde de la lumière. Nous aurons obtenu l'égalité chromatique du grossissement.
On peut l'exprimer aussi en disant que la distance focale résultante ne dépendra pas de la longueur d'onde. Les distances focales dans le rouge et dans le bleu sont égales (B Fb = R Fr).
La distance focale d'une lentille mince est donnée par la formule :
 [1]
[1]n est l'indice de réfraction du verre, R1 et R2 sont les rayons de courbure de la première et de la deuxième face de la lentille. A est la courbure totale de la lentille, c'est la différence des inverses des rayons de courbure.
Comme nous l'avons démontré dans une autre page, la distance focale d'un groupe de deux lentilles minces est donnée par la relation suivante :
 [2]
[2]F est la distance focale résultante, f1 et f2 les distances focales des deux lentilles et e est la distance qui les sépare.
Démonstration de la règle de Huygens utilisant les dérivées
Je vous propose une première démonstration qui nécessite la connaissance des dérivées de fonctions mathématiques.
Exprimons la relation [2] sous la forme équivalente suivante :
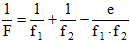 [3]
[3]Associons les deux équations [1] et [3]:
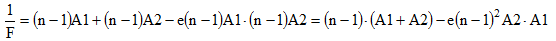 [4]
[4]Pour obtenir l'égalité chromatique du grossissement, il faut que la distance focale ne varie pas en fonction de l'indice de réfraction. La dérivée de cette expression par rapport à la longueur d'onde λ doit donc être nulle :
 [5]
[5]ceci correspond à
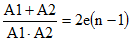 [6]
[6]Or l'équation [1] nous indique que :
 [7]
[7]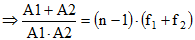 [8]
[8]Rapprochons cette expression de l'équation [6] et nous obtenons :
 [9]
[9]Divisons les deux termes de l'égalité par (n-1) :
- 2e = f1 + f2 [10]
Démonstration de la règle de Huygens sans utiliser les dérivées
N'oublions pas que la technique des dérivées en mathématiques n'existait pas encore à l'époque de Christiaan Huygens.
On pourra estimer que je détaille trop la démonstration suivante. C'est parce que je crains que certains soient grandement surpris par mes affirmations. Je dois donc les justifier systématiquement.
Rappelons notre équation [2]
 [2]
[2]F est la distance focale résultante, f1 et f2 les distances focales des deux lentilles et e est la distance qui les sépare.
Une petite variation de la longueur d'onde de la lumière provoque une même variation relative de la longueur focale de chaque lentille mais nous voulons que la distance focale résultante reste inchangée.
Sous l'effet de la petite variation de longueur d'onde la distance focale de la première lentille devient (1+ε).f1 et la distance focale de la deuxième lentille devient (1+ε).f2.
Nous voulons que F reste inchangée malgré cette petite variation. Par conséquent, un accroissement ε de la distance focale de chacune des deux lentilles ne doit pas entrainer de changement de F :
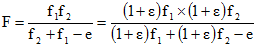 [11]
[11]Regroupons les facteurs :
 [12]
[12]Divisons chacun des deux termes de l'égalité par le produit f1.f2 :
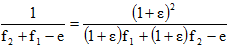 [13]
[13]Dans l'expression de droite, divisons le numérateur et de dénominateur par (1+ε) :
 [14]
[14]Or puisque ε est très petit, nous pouvons considérer que diviser par (1+ε) équivaut à multiplier par (1-ε). Ce qui nous donne :
 [15]
[15]Développons :
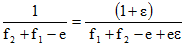 [16]
[16]Dans l'expression de droite, nous multiplions le numérateur et le dénominateur par (1-ε) en considérant que (1-ε).(1+ε) = 1 puisque ε est très petit et son carré est négligeable.
 [17]
[17]Inversons les deux termes et l'égalité est encore valide :
- f1 + f2 - e = (1 - ε)(f1 + f2 - e) + eε(1 - ε) [18]
Le carré de ε étant négligeable, nous pouvons affirmer que eε(1-ε) = eε. Nous avons donc :
- f1 + f2 - e = (1 - ε)(f1 + f2 - e) + eε [19]
Développons :
- f1 + f2 - e = f1 + f2 - e - ε(f1 + f2 - e) + eε [20]
Retranchons (f1+f2-e) de chaque côté de l'égalité :
- 0 = -ε(f1 + f2 - e) + eε [21]
Divisons les deux termes par -ε :
- 0 = f1 + f2 - 2e [22]
Autrement exprimé :
- 2e = f1 + f2 [23]
Nous venons de retrouver la règle de Christiaan Huygens
Cette seconde démonstration nous rappelle d'une façon plus évidente que cette règle est valide seulement pour un petit domaine spectral. Plus ce dernier est large et moins le résultat est valide.
Conclusion
Un oculaire à deux lentilles, faites du même verre, est corrigé de l'inégalité chromatique du grossissement si la somme des distances focales des deux lentilles est égale au double de la distance qui les sépare.
Avant d'employer ce résultat, il faut bien se rappeler que nous avons fait des approximations pour l'obtenir : Nous avons considéré des lentilles minces et un "petit" domaine spectral.