NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
Grossissement et grandissement
Les instruments d'observation astronomique fournissent des images en leur foyer (primaire ou secondaire) qui méritent d'être observées de près ou qui doivent être agrandies afin de les enregistrer photographiquement avec une meilleure résolution.
Nous allons commencer par faire une distinction entre les différents concepts.
La notion de grossissement est employée pour l'observation visuelle avec un instrument optique, elle peut être considérée de différentes façons :
- - A l'il nu, nous obtenons une image de l'objet observé sur notre rétine. A l'aide d'un instrument d'observation, nous obtenons sur la rétine une image d'une autre taille (généralement, elle est plus grande). On appelle grossissement le rapport qu'il y a entre la dimension de l'image sur la rétine vue à travers l'instrument et celle obtenue à l'il nu.
Bien entendu, cette conception est théorique puisque on ne peut habituellement pas mesurer directement la dimension de l'image sur la rétine.
- Avec un instrument d'observation, on voit un objet comme s'il était situé à une distance différente (généralement, elle est plus petite).
On considère que le grossissement est le rapport entre ces deux distances. Ainsi, une longue-vue qui grossit 20 fois permet d'observer un objet éloigné comme s'il était placé à une distance 20 fois moins grande.
Pour les petits objets, on considère par convention que l'il humain fournit des images nettes en s'approchant jusqu'à 250mm de l'objet observé. Le grossissement d'un microscope se rapporte donc à cette distance. Ainsi, un microscope grossissant 100 fois permet d'obtenir sur la rétine une image semblable à celle qu'on aurait, si cela était possible, en approchant l'il à la distance de 2,5mm de l'objet (=250/100).
- En fait, les considérations ci-dessus montrent que le grossissement est une affaire d'angles. Admettons que la dimension angulaire d'un objet est définie par l'angle formé par les points extrêmes de l'objet et l'il de l'observateur. Vu à travers un instrument d'observation, la dimension angulaire de cet objet est différente (généralement, elle est plus grande). On appelle grossissement le rapport entre ces deux dimensions angulaires.
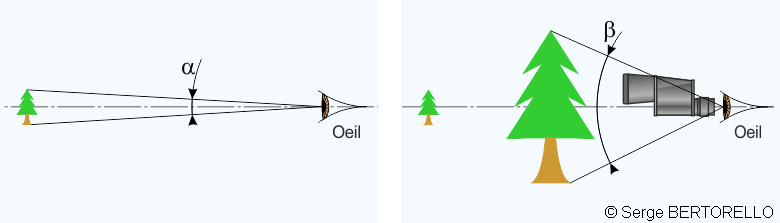
L'objet est aperçu à l'il nu avec une dimension angulaire α. Avec un instrument grossissant, il apparaît avec la dimension angulaire β.
La valeur du grossissement peut être modifiée en changeant l'oculaire de l'instrument.
Considérons le schéma suivant qui représente une lunette astronomique.

L'axe optique de l'instrument (en noir) passe par le centre C de l'objectif, par le foyer F de l'objectif et par le centre O de l'oculaire représenté ici par une lentille simple.
Le segment Fi représente la dimension de l'image d'un objet qui est vu à l'il nu sous un angle α, cet objet est vu à travers l'oculaire sous l'angle β.
La longueur du segment CF est égale à la distance focale F image de l'objectif.
La longueur du segment OF est égale à la distance focale f objet de l'oculaire.
Nous allons considérer que les angles α et β sont petits, ce sont les conditions de Gauss. Par conséquent, nous pourrons aussi considérer que la valeur de chacun de ces angles (en radian) est égale à la valeur de sa propre tangente.
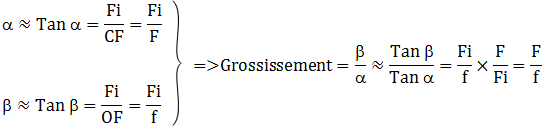
Le grossissement d'une lunette astronomique s'obtient donc en divisant la distance focale de l'objectif par la distance focale de l'oculaire.
Pour être complet, il faudrait aussi tenir compte des signes car dans ce montage la distance focale objet de l'un possède un signe différend de la distance focale image de l'autre. On trouverait ainsi une valeur négative pour le grossissement qui correspond au fait que l'image est inversée.
Ce raisonnement peut être appliqué à la plupart des instruments astronomiques. Pour les instruments plus complexes, comme les longues vues avec leur véhicule, il faut donner à F la valeur de la distance focale résultante.
Un lecteur attentif pourra répliquer en disant que j'ai considéré ici que les angles sont "petits" et donc la formule obtenue est critiquable si les angles sont plus grands. En effet, le grossissement pourrait varier lorsqu'on s'écarte de l'axe. Cela signifierait que l'instrument souffre d'une aberration nommée distorsion que nous avons évoquée dans un précédent exposé.
En conclusion, la formule du grossissement G=F/f est définie pour des petits angles (optique paraxiale) et ne tient jamais compte de la distorsion.
Remarquez-bien que les définitions précédentes montrent que l'expression "grossissement" ne peut pas être employée pour une photographie.
Pour le cliché d'un petit objet, on peut employer la notion de "grandissement" car il y une relation logique entre les dimensions de l'objet et celles de son image (le grandissement est le rapport entre ces deux dimensions).
L'échelle d'une carte ou d'un cliché
Pour la photographie d'un objet éloigné, nous avons vu que la notion de grossissement n'est pas adaptée et, de plus, la notion de grandissement est absurde. Par exemple : la comparaison entre la dimension d'une galaxie (une centaine de milliers d'années-lumière) et la dimension de son image sur le cliché (quelques millimètres) n'aboutit pas à un résultat intéressant...
Pour caractériser la dimension de la carte ou de la photographie d'une portion du ciel, on indique son échelle angulaire, c'est à dire la correspondance entre une valeur angulaire sur le ciel et une longueur mesurée sur la carte ou sur l'image (exemple : 1 degré par centimètre = 1°/cm). Avec un capteur électronique on pourra faire allusion aux dimensions des photosites ou des pixels (exemple : 5 secondes d'arc par pixel = 5"/pixel).
Parfois, on indique simplement la dimension angulaire du champ que la photo représente sur le ciel.
Observation visuelle : Les oculaires
L'image fournie par l'objectif de l'instrument d'observation est petite et l'il nu ne peut pas en apprécier tous les détails.
On considère conventionnellement qu'un il humain peut voir un objet avec netteté en s'approchant de lui jusqu'à 25cm. Cela signifie, par exemple, que l'image d'un objet lointain qui serait formée par un objectif de 1m (ou 100cm) de distance focale et examinée par un il placé à 25 cm de celle-ci serait perçue avec un grossissement de 4 fois (100 / 25 = 4). C'est bien peu sans compter que, dans ces conditions, la plus grande partie des rayons lumineux recueillis par l'objectif ne sont pas utilisés.
Dans le but d'agrandir l'image pour l'observation visuelle dans de bonnes conditions, on va transformer l'image focale réelle en une image virtuelle destinée à l'il de l'observateur. Pour cela, on peut envisager deux types de dispositifs :
- - L'oculaire divergent : Il s'agit d'une lentille divergente placée avant le foyer. Si l'objectif seul fournit une image inversée, celle-ci est vue droite avec l'oculaire divergent. C'est l'oculaire de la lunette de Galilée. Il n'est quasiment plus employé de nos jours.
- L'oculaire convergent : Dans le principe, il s'agit tout simplement d'une loupe disposée après le foyer qui permet une analyse détaillée de l'image focale de l'objectif. Si l'objectif seul fournit une image inversée, celle-ci est vue inversée avec ce type d'oculaire. Il en existe une grande variété avec des performances diverses et des coûts très variés...
Quel que soit le type auquel il appartient, un oculaire est caractérisé par sa distance focale. Le grossissement G de l'instrument sur lequel on l'emploie est déterminé par la relation suivante :

avec
F = distance focale de l'objectif
f = distance focale de l'oculaire
Dans ce qui suit, nous évoquerons seulement les oculaires convergents. Leur distance focale est habituellement comprise entre 4 et 50mm.
Remarque au sujet des oculaires pour microscopes :
Les amateurs d'astronomie peuvent être tentés d'employer des oculaires de microscope sur leur instrument d'observation du ciel. C'est bien naturel, surtout qu'on peut trouver ces oculaires d'occasion à très petit prix. Problème : leur distance focale n'est pas indiquée (ou rarement), au lieu de cela on trouve une indication de grossissement sous la forme d'un nombre suivi de la lettre "x". Pour comprendre cela, il faut se rappeler que l'oculaire est une loupe et son grossissement est comparé à ce que l'il humain peut voir depuis la plus petite distance conventionnelle de vision nette, soit 250mm.
Pour déterminer la distance focale de l'oculaire, il suffit donc de diviser 250mm par son grossissement.

avec
f = distance focale de l'oculaire en mm
g = grossissement de l'oculaire
Ceci étant dit, je dois tenter de tempérer l'enthousiasme de ceux qui voudraient employer un oculaire de microscope sur un télescope car ces accessoires ne sont pas prévus pour des grandes ouvertures (ou petits rapports F/D). On arrive quand même à trouver de bonnes occasions : à mes débuts j'avais acheté un oculaire orthoscopique de microscope de 17x pour 10 francs, il me sert encore aujourd'hui.
Généralement, ce sont plutôt des oculaires de Huygens, Dollond ou Kellner.
Le grossissement n'est donc pas une caractéristique de la lunette astronomique ou du télescope, c'est une grandeur que l'on doit adapter à l'objet que l'on observe par un choix de l'oculaire.
Ainsi, on peut souhaiter un faible grossissement pour étudier un astre étendu ou pour faire une recherche d'un objet faible.
Pour observer les fins détails de la surface d'une planète, on choisira le grossissement maximal en fonction des circonstances (turbulence atmosphérique, luminosité de l'astre, contraste des détails, ...).
Pour séparer les composantes serrées d'une étoile double, on utilisera le grossissement maximal possible.
En augmentant le grossissement, on affaiblit la luminosité de l'image d'un objet étendu et du fond du ciel mais pas celle d'un objet ponctuel comme une étoile. Ainsi, par un choix judicieux de la longueur focale de l'oculaire, on peut optimiser le contraste de l'image pour la recherche d'un objet faible.
Ce sont là des principes généraux qui guident l'observateur pour choisir le grossissement. Pour chaque observation, l'astronome devra choisir le meilleur compromis en fonction des circonstances. Il appréciera pour cela d'avoir une "nombreuse" collection d'oculaires.
Le grossissement minimal d'un instrument :
Il existe un grossissement minimal en dessous duquel il n'est pas intéressant d'utiliser une lunette ou un télescope. On considère généralement que c'est le grossissement qui fournit une pupille de sortie de six millimètres de diamètre, c'est le diamètre conventionnel que prend la pupille de l'il humain dans l'obscurité. Dans ce cas, notre il profite de l'intégralité de la lumière qui pénètre dans l'instrument (observation nocturne). Avec un grossissement plus faible, on perdrait une partie de la lumière qui ne pénètrerait pas dans l'il.

Exemples :
- - une lunette de 60 mm devra être utilisée avec un grossissement supérieur ou égal à 10 fois.
- un télescope de 150 mm devra être utilisé avec un grossissement supérieur ou égal à 25 fois.
Bien entendu, pour une personne âgée ces valeurs doivent être modifiées. Il faut dans ce cas rechercher une pupille de sortie de trois ou quatre millimètres de diamètre.
Le grossissement maximal d'un instrument :
De même, il existe aussi une limite maximale au grossissement. En effet, si le faisceau lumineux qui entre dans l'il est trop étroit, il est dispersé par les défauts de la cornée et du cristallin. La limite généralement admise est 0,4 millimètre pour le diamètre de la pupille oculaire. Heureusement, le grossissement correspondant est largement suffisant pour nous permettre de voir tous les détails que donne l'objectif.
- Grossissement maxi = (diamètre de l'objectif en millimètres) x 2,5
Exemples :
- une lunette de 60 mm devra être utilisée avec un grossissement inférieur ou égal à 150 fois.
- un télescope de 150 mm devra être utilisé avec un grossissement inférieur ou égal à 375 fois.
Je vous invite donc à vous méfier d'une brochure commerciale qui donnerait des indications au-delà de ces valeurs...
Le grossissement résolvant (appelé aussi grossissement utile) :
C'est le grossissement qui permet à un il normal de distinguer tous les plus fins détails fournis par l'objectif. Ainsi, un télescope de 12cm de diamètre sépare des détails de 1 seconde d'arc (voir Pouvoir séparateur des instruments d'observation). Avec un grossissement de 60 fois, il nous montre ces détails avec un écart d'une minute d'arc. Ceci permet donc à un il normal de les distinguer car le pouvoir de résolution d'un il normal est de 1 minute d'arc.
Par convention, pour définir le grossissement résolvant, on prend une marge de sécurité et on considère avec pessimisme que l'il a un pouvoir séparateur de 2 minutes d'arc. Ainsi dans notre exemple le grossissement résolvant est de 120 fois. Ce grossissement résolvant d'un télescope ou d'une lunette est numériquement égal au diamètre de l'instrument exprimé en millimètres. Notez que je vais utiliser cette définition dans la suite de cet exposé mais d'autres auteurs peuvent choisir une considération différente.
En suivant cette définition, on constate que le grossissement résolvant est obtenu avec un oculaire dont la distance focale en millimètres s'exprime avec le même nombre que le rapport d'ouverture F/D de l'objectif. Ainsi, avec une lunette ouverte à F/D=15, nous obtiendrons le grossissement résolvant avec un oculaire de 15mm. De même, un télescope ouvert à F/D=4 donnera son grossissement résolvant avec un oculaire de 4mm.
Oculaires constitués d'une seule lentille : Oculaire de Kepler
Johannes Kepler est né le 27 décembre 1571 près de Stuttgart (Allemagne) et il est mort le 15 novembre 1630 à Ratisbonne en Bavière.
Tels que les a définis leur inventeur Kepler, les premiers oculaires convergents étaient composés d'une seule lentille. C'était vraiment une simple loupe avec laquelle on étudiait l'image fournie par un objectif qui était lui-même une lentille simple de très grande distance focale (Exemple : la focale pouvait avoir plus de 10m pour un diamètre de 10cm).
Dans ces conditions, les astronomes ont pu faire des découvertes fondamentales mais aujourd'hui le contexte est tout à fait différent. En effet, les astronomes cherchent désormais à obtenir des images performantes avec des instruments compacts. Comme nous allons le voir, ce but est incompatible avec l'emploi d'une lentille simple en guise d'oculaire car le résultat serait entaché de graves aberrations (chromatique, de sphéricité, distorsion, astigmatisme, coma).
L'examen de cet oculaire simple va nous permettre d'évoquer les différentes grandeurs qui caractérisent ce type d'accessoire.
Comme chacune des illustrations suivantes, la figure 2 montre la constitution d'un oculaire de 10mm de distance focale avec une échelle graduée qui permet de juger ses dimensions.

Ici il s'agit d'une lentille équiconvexe, mais à l'origine, elle avait une forme plan-convexe avec la face plane tournée vers l'il.
La lumière vient de l'objectif situé à gauche de la figure qui forme une image réelle sur son plan focal.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
Quand l'oculaire est correctement placé, il fournit derrière-lui une image de l'objectif qu'on appelle la "pupille oculaire" ou "l'anneau oculaire". C'est précisément à cet endroit que l'observateur doit placer la pupille de son il pour obtenir les meilleures conditions d'observation.
La distance entre la pupille oculaire et la dernière surface de verre (le dernier dioptre) se nomme "dégagement oculaire". Parfois, on l'appelle aussi "tirage d'anneau" ou même "relief d'il". Cette dernière expression vient d'une mauvaise traduction du terme anglais correspondant.
Si un porteur de lunettes veut observer sans se défaire de ses verres correcteurs, il doit employer un oculaire qui dispose d'un long dégagement oculaire. Toutefois, pour l'observation astronomique à l'oculaire, je déconseille de garder les lunettes sur le nez car la mise au point peut corriger le défaut de vue. Seuls les forts astigmates devront conserver leurs verres correcteurs lors des observations à faible grossissement.
Hormis ce cas spécial, je considère qu'un grand dégagement oculaire n'est pas souhaitable même si les débutants le préfèrent, car il oblige à maintenir l'il loin de l'oculaire, ce qui est incommode. Moi-même, je préfère garder le contact avec la monture de l'oculaire par l'intermédiaire des sourcils ou de la peau. Ainsi, je peux m'assurer de conserver longtemps la bonne position. Quand il n'y a pas ce contact, il est très difficile de maintenir l'il au bon endroit, il faut sans-cesse rechercher la bonne position et on se fatigue extrêmement vite.
La monture de l'oculaire doit être conçue pour compenser le dégagement oculaire s'il est excessif.
En comparaison avec les types que nous allons examiner ensuite, l'oculaire de Kepler possède un dégagement oculaire important (il est approximativement égal à sa distance focale).
C'est le champ de vision procuré par l'oculaire, il est habituellement limité par le trou d'un diaphragme de champ. Celui-ci masque le bord du champ où les images sont de mauvaise qualité.
On exprime le champ d'un oculaire avec l'angle formé par l'il et les bords du champ.
Un oculaire fournit ses meilleures images au centre de son champ, c'est à dire sur l'axe optique, et la qualité se dégrade au fur et à mesure qu'on s'en éloigne. Le graphique disposé à droite de la figure 2 nous permet d'évaluer cette dégradation.
On appelle coulant de l'oculaire la partie cylindrique que l'on doit glisser dans le porte-oculaire de l'instrument et par lequel cet accessoire est maintenu.
Le diamètre du coulant est normalisé selon les valeurs du tableau suivant :
Pour illustrer les performances des oculaires présentés dans cet exposé, je propose sur la droite de chaque figure un graphique dont les courbes montrent la plus grande dimension des images stellaires obtenues avec le grossissement résolvant en fonction de la distance à l'axe optique mesurée dans le champ de l'oculaire. Chacun de ces graphes est issu d'une simulation informatique.
Les instruments considérés ici sont des télescopes de Newton de 1m de distance focale. J'ai choisi ce type d'instrument car il est très bien défini et qu'il n'a pas d'aberration chromatique.
Les différentes courbes de couleurs correspondent à des rapports d'ouvertures différents et des distances focales d'oculaires choisies pour obtenir le grossissement résolvant. Ainsi, la courbe attribuée au rapport F/D=15 est obtenue avec un oculaire de 15mm et un objectif de 66,66mm de diamètre, la courbe du rapport F/D=10 est réalisée avec un oculaire de 10mm et un objectif de 100mm de diamètre, et ainsi de suite. Ainsi, nous considérons toujours le grossissement résolvant car nous utilisons systématiquement un oculaire dont la distance focale en millimètres est égale numériquement au rapport d'ouverture F/D de l'instrument.
Les courbes en trait plein correspondent à la plus grande dimension de l'image stellaire en considérant le domaine spectral entre 480nm et 656nm. Ce domaine spectral est très étendu en comparaison avec le chromatisme résiduel des lunettes astronomiques. Si j'avais choisi une lunette astronomique pour la simulation, ces courbes auraient été trop dégradées par son chromatisme résiduel.
Les courbes en pointillé sont obtenues en considérant uniquement la longueur d'onde de 546nm qui correspond approximativement au maximum de la sensibilité spectrale de l'il humain. Ces courbes pointillées sont tracées avec la même couleur que le trait plein et le nombre d'ouverture auxquels elles correspondent.
Le graphe de la figure 2 nous montre que l'oculaire de Kepler est décevant. Il fournit des images acceptables uniquement près de l'axe optique avec un objectif de faible ouverture (grand rapport F/D).
Il n'est plus employé de nos jours pour l'observation astronomique.
Oculaires constitués avec deux lentilles simples
Christiaan Huygens était un physicien néerlandais (1629 - 1695), il a proposé de remplacer l'oculaire de Kepler par une combinaison de deux lentilles taillées dans le même verre qui corrige les aberrations hors de l'axe ainsi que l'aberration chromatique du grossissement.
Tout d'abord, je vous propose sur une page séparée le calcul de la distance focale d'un groupe de deux lentilles. Le résultat s'exprime avec la formule suivante :

Dans cette expression, F représente la distance focale résultante d'un groupe de deux lentilles simples de distances focales f1 et f2 espacées par la distance e.
J'expose sur une autre page le calcul qui conduit à la règle de Christiaan Huygens que doivent satisfaire les deux lentilles pour former un oculaire corrigé de l'inégalité chromatique du grossissement. Il s'agit de la condition suivante :
- 2e = f1 + f 2
Autrement dit : Un oculaire à deux lentilles, faites du même verre, est corrigé de l'inégalité chromatique du grossissement si la somme des distances focales des deux lentilles est égale au double de la distance qui les sépare.
On oublie trop souvent que ces deux formules ont été établies en partant de quelques approximations, elles ne sont donc pas des relations exactes. En les suivant lors de la conception d'un oculaire, on obtient une distance focale qui peut être légèrement supérieure (suivant le type de combinaison) et le résultat obtenu peut être sensiblement amélioré en optimisant la distance entre les lentilles.
Vous pourrez accéder aux caractéristiques de fabrication d'un oculaire en cliquant sur l'image qui le représente.
La règle qu'il a définie a guidé Christiaan Huygens pour concevoir la formule d'oculaire qui porte son nom. Dans l'oculaire de Huygens, la première lentille appelée "verre de champ" a une longueur focale égale à 4 unités. Une distance de 3 unités la sépare de la deuxième lentille, le verre d'il, dont la distance focale vaut 2 unités. On exprime cette formule par la série [4-3-2]. Sa distance focale vaut 8/3 de l'unité considérée.
Cet oculaire vérifie bien la règle de Huygens puisque : 2 x 3 = 4 + 2

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
L'illustration nous montre que la lentille de champ de l'oculaire de Huygens est disposée avant le foyer, c'est pour cela qu'on le qualifie d'oculaire négatif.
Nous constatons aussi que le dégagement oculaire est plus court que pour l'oculaire de Kepler.
Son champ est habituellement limité entre 30° et 40° par un diaphragme.
Le graphique de droite indique que cet oculaire est plus performant que le précédent car il fournit une image nette sur un plus grand champ. Il faut toutefois admettre qu'il n'est pas raisonnable de l'employer sur des instruments qui ont un rapport F/D inférieur à 15.
Cette formule peut être considérée comme une variante de celle de Huygens avec laquelle on la confond souvent. On la doit à John Dollond (1706 - 1761) qui l'a conçue selon la formule [3-2-1].

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
Cet oculaire ressemble à celui de Huygens mais en plus mauvais pour la finesse des images. Il est donc étonnant de constater qu'il est beaucoup plus utilisé que celui de Huygens.
La lentille de champ disposée avant le foyer en fait un oculaire négatif.
Le dégagement oculaire est peu différent de celui de l'oculaire de Huygens.
Son champ est habituellement limité entre 30° et 40° par un diaphragme.
Il ne faut pas employer l'oculaire de Dollond sur des instruments qui ont un rapport F/D inférieur à 15.
Remarque : En démontant des oculaires de Huygens ou de Dollond du commerce, j'ai souvent constaté que les lentilles étaient équiconvexes. Cette disposition dégrade la qualité des images et elle est contraire aux recommandations de Huygens et Dollond qui préconisaient des lentilles plan-convexes avec la convexité dirigée vers l'objectif.
Cet oculaire constitué par deux lentilles identiques a été conçu par Jesse Ramsden (1735-1800).
Si les deux lentilles ont la même distance focale, la règle de Christiaan Huygens que nous avons vu plus haut nous indique qu'elles doivent être séparées par la valeur de leur distance focale pour obtenir la formule [1-1-1]. Cela entraîne deux conséquences gênantes :
- - La lentille de champ est au foyer image de la lentille d'il. On voit donc nettement les poussières ou les rayures qui peuvent éventuellement être présentes sur sa surface.
- Le dégagement oculaire est nul. Il est donc impossible de disposer l'il sur la pupille de sortie.
C'est pour cela qu'on rapproche habituellement les lentilles aux 2/3 environ de la distance focale. La formule devient [3-2-3] et elle ne satisfait plus à la condition définie par Huygens. Pourtant le résultat est favorable et les performances de cet oculaire sont sensiblement meilleures que celles des précédents.
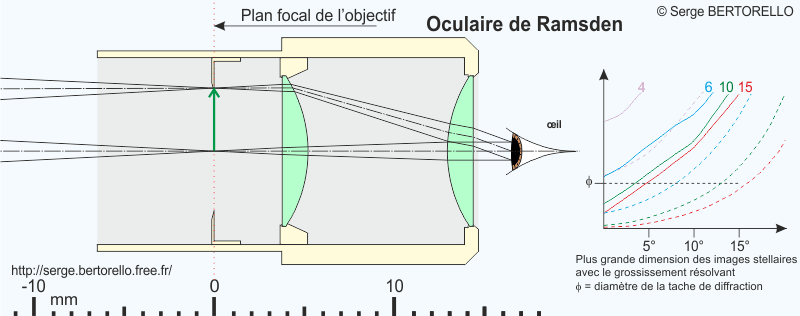
Parfois le diamètre de la lentille d'il est plus petit que celui de la lentille de champ mais elles doivent avoir la même distance focale. La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée après le foyer en fait un oculaire positif, on peut donc envisager de l'équiper d'un réticule au niveau du diaphragme de champ.
Le dégagement oculaire peut être ajusté en jouant sur la distance entre les lentilles mais il est plus court que celui de l'oculaire de Huygens.
Son champ est habituellement limité entre 30° et 40° par un diaphragme.
On peut employer l'oculaire de Ramsden sur des instruments dont le rapport F/D est égal ou supérieur à 8.
Les oculaires précédents sont limités aux instruments faiblement ouverts à cause de leur aberration chromatique résiduelle et des limitations de leur champ. Aujourd'hui, pour l'observation astronomique, on ne les trouve plus que dans les instruments économiques.
Toutefois, ils sont encore très appréciés quand on les utilise sur des microscopes... mais ce n'est pas notre sujet.
Nous allons maintenant examiner des oculaires dont les lentilles sont constituées de verres différents.
Le choix des verres associé à un plus grand nombre de lentilles permet à l'opticien de mieux corriger les aberrations sur un grand champ.
La plupart des livres qui présentent l'optique astronomique font allusion à plusieurs types d'oculaires achromatiques (Erfle, Bertele...) qu'on ne rencontre jamais (dans la réalité?). De plus, mes simulations informatiques m'ont clairement montré que ces solutions sont dénuées d'intérêt pour l'observation astronomique. Je n'en parlerai donc pas.
Cet oculaire conçu par Carl Kellner (1829-1855) est analogue à un oculaire de Ramsden dans lequel la lentille d'il est remplacée par un doublet avec élément divergent à l'extérieur.
Cet oculaire est très répandu notamment dans les jumelles et dans les longues-vues. C'est le plus économique des oculaires achromatiques.
L'opticien peut choisir d'employer deux ou trois verres différents pour réaliser ses trois lentilles.
La formule et ses qualités varient selon le choix des verres pour la composition de ses lentilles mais les performances sont toujours intéressantes. On rencontre parfois des oculaires de Kellner avec une lentille de champ équiconvexe au lieu de la forme plan-convexe préconisée, cela apporte des aberrations qui dégradent la qualité des images au bord du champ.
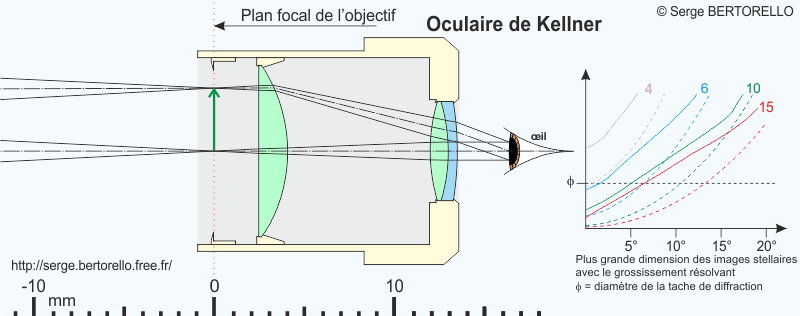
La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée après le foyer en fait un oculaire positif, on peut donc envisager de l'équiper d'un réticule au niveau du diaphragme de champ.
Le dégagement du cercle oculaire est confortable, il est comparable à celui de l'oculaire de Huygens.
On limite habituellement son champ à 40° environ.
On peut employer l'oculaire de Kellner sur des instruments dont le rapport F/D est égal ou supérieur à 8.
C'est le physicien allemand Ernst Abbe (1840-1905) qui a conçu cet oculaire en cherchant à minimiser la distorsion, c'est cette caractéristique qui lui donne le qualificatif "orthoscopique". Toutefois, cette qualité ne le rend pas particulièrement intéressant pour l'observation astronomique car les autres formules d'oculaires communément employées ne sont pas affectées par une distorsion inconvenante.
L'oculaire orthoscopique s'apparente à l'oculaire de Ramsden. Sa lentille de champ est composée d'un triplet sur-corrigé constitué par 3 lentilles accolées. On a besoin de trois verres différents pour réaliser ses quatre lentilles.
Parmi les différentes versions de cet oculaire que j'ai étudiées, aucune ne possède des performances qui se démarquent nettement de celles d'un bon oculaire de Kellner. Vous comprendrez donc que je n'ai pas une bonne opinion pour cette formule.
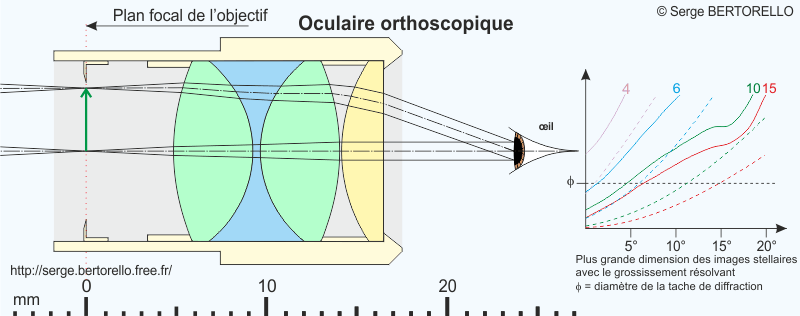
La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée après le foyer en fait un oculaire positif, on peut donc envisager de l'équiper d'un réticule au niveau du diaphragme de champ.
Le dégagement du cercle oculaire est plus long que pour les formules précédentes.
Son champ est habituellement limité à 40° environ (parfois 45°).
On peut employer l'oculaire orthoscopique sur des instruments dont le rapport F/D est égal ou supérieur à 6.
Cet oculaire conçu par Georg Simon Plössl (1794-1868) est analogue à un oculaire de Ramsden dans lequel chaque lentille est constituée par un doublet avec élément divergent à l'extérieur. Ces deux doublets doivent être identiques mais parfois l'opticien réduit le diamètre de celui qui est proche de l'il. Comme l'achromatisme ne dépend pas de la position des lentilles, on rapproche celles-ci au maximum.
Deux verres différents sont nécessaires pour réaliser les quatre lentilles.
La formule et ses qualités varient légèrement selon le choix des verres pour la composition de ses lentilles mais les performances sont toujours intéressantes.

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée après le foyer en fait un oculaire positif, on peut donc envisager de l'équiper d'un réticule au niveau du diaphragme de champ.
Le dégagement du cercle oculaire est confortable, il est comparable à celui de l'oculaire orthoscopique.
Son champ est habituellement limité à 50° environ.
C'est mon type d'oculaire préféré, je l'emploie sur des télescopes dont le rapport F/D est compris entre 4 et 5.
Cet oculaire à grand champ a été conçu par Al Nagler, fondateur de la société Televue.
Deux verres différents sont nécessaires pour réaliser ses sept lentilles.
C'est un dispositif encombrant et lourd. Pour illustrer un modèle de 10mm de distance focale sur la figure suivante, je n'ai pas pu conserver l'échelle des illustrations précédentes.

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée avant le foyer en fait un oculaire négatif, on ne peut donc pas envisager de l'équiper d'un réticule.
Les porteurs de lunettes apprécient le dégagement de son cercle oculaire qui est très grand.
Son champ est habituellement limité à 75° environ.
Cet oculaire de Nagler a fait une apparition très remarquée dans le milieu des astronomes amateurs français pendant les années 1980. On peut l'employer sur des télescopes très ouverts (c'est à dire avec un petit rapport F/D).
Il s'agit du premier oculaire à grand champ qui est devenu populaire. Ce type de dispositif répond à différentes demandes d'observateurs :
- - Les utilisateurs des télescopes de Dobson devenant de plus en plus nombreux désirent des oculaires à grand champ pour pallier aux difficultés de pointage de leur instrument qui n'a bien souvent pas de mécanisme de suivi. Ces oculaires permettent de profiter du spectacle quelques instants entre chaque repointage du télescope.
- Certains objets célestes fournissent un très beau spectacle à travers ces oculaires qui permettent d'oublier les limites du champ même si les bords de celui-ci ne sont pas aussi nets que le centre...
La combinaison optique de cet oculaire se compose d'un ensemble divergent semblable à une lentille de Barlow (voir plus loin) suivie par un groupe de lentilles convergent qui permet d'analyser l'image ainsi agrandie. Cette disposition a été ensuite reprise pour d'autres formules à grand champ.
Il faut noter que ce premier oculaire de Nagler souffre d'une forte aberration de sphéricité sur sa pupille de sortie. Cela a pour conséquence un agrandissement "très important" de cette pupille de sortie, il ne faut donc pas l'employer pour les faibles grossissements surtout quand le rapport F/D est petit sinon on perdrait de la lumière (comme si on avait diminué les dimensions de l'objectif).
Comme pour toutes les autres catégories d'oculaires, il faut centrer dans son champ l'objet observé pour bénéficier de la meilleure résolution de l'image mais avec ce dispositif à grand champ est apparue une nouvelle préoccupation. En effet, le champ visuel de cet oculaire est si étendu qu'il est très difficile de déterminer son centre et donc de centrer l'image.
Ceci est particulièrement critique pour son emploi sur les télescopes azimutaux qui n'ont pas de système d'entraînement motorisé. Dans ce cas, l'observateur place l'objet à une extrémité du champ et il profite pour son observation du temps que met l'astre pour traverser le champ sous l'influence de la rotation de la Terre. Cette pratique ne permet pas de profiter des meilleures images.
Cet oculaire à grand champ a été conçu par Al Nagler, fondateur de la société Televue. Il est moins encombrant et moins lourd que le précédent et il fournit de meilleures images.
Cinq verres différents sont nécessaires pour réaliser ses huit lentilles.

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée avant le foyer en fait un oculaire négatif, on ne peut donc pas envisager de l'équiper d'un réticule.
Le dégagement de son cercle oculaire est confortable mais il n'est pas compatible avec le port des lunettes.
Son champ est habituellement limité à 80° environ.
Cet oculaire forme des images plus fines que le Nagler 1 et il supporte mieux les objectifs de grande ouverture (petits rapports F/D).
Sa pupille de sortie ne souffre pas de l'aberration de sphéricité du Nagler 1, il est donc possible de l'employer pour les faibles grossissements.
Par contre, on peut lui faire la même remarque en ce qui concerne la difficulté de centrer l'objet observé sur la zone de meilleure image.
En fait, Al Nagler a défini toute une famille d'oculaires dont les formules optiques s'apparentent à celles que nous venons d'examiner (Exemple : US Patent N°4286844 et N°4747675).
Depuis le début des années 2000, un nouveau type d'oculaire à grand champ est devenu à la mode dans le monde des astronomes amateurs, il s'agit de la formule Ethos qui a été conçue par Paul Dellechiaie, ingénieur de la société Televue.

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée avant le foyer en fait un oculaire négatif, on ne peut donc pas envisager de l'équiper d'un réticule.
Huit verres différents sont nécessaires pour réaliser ses neuf lentilles.
Il fournit un champ visuel de 100° et, pour le parcourir, l'il de l'observateur doit fortement pivoter pour regarder dans les coins...
Son champ est plus grand que celui des Nagler et ses images sont globalement meilleures. Toutefois, son chromatisme résiduel est plus important pour les grandes ouvertures (ou petits rapports F/D) même au centre du champ.
C'est au centre de son champ visuel que ses images ont la meilleure qualité mais comment centrer un objet dans un espace aussi vaste ?
Les oculaires Ethos sont imposants : L'oculaire Ethos 21mm a un poids de 1020g alors que le Nagler de 22mm "ne pèse que 680g". De plus, les images ci-dessus permettent de comparer les dimensions de ces deux types. C'est donc du lourd! Il faut que l'instrument sur lequel on veut l'employer puisse le supporter et aussi... que son porte-oculaire soit assez costaud et qu'il le maintienne suffisamment bien afin ne pas le laisser tomber...
Depuis quelques années, on voit fleurir dans le commerce quantité d'offres d'oculaires à grand champ. Je ne les ai pas toutes essayées ou je n'ai pas réussi à avoir leurs caractéristiques de fabrication, je ne peux donc pas les joindre à ce comparatif.
Quelquefois ces oculaires sont des formules déjà connues par ailleurs que l'on renomme en leur attachant le nom d'une marque avec une référence qui ne dit rien sur l'origine du concepteur. Exemple : La marque MEADE propose une gamme d'oculaires "UWA" qui ressemblent beaucoup au Nagler 2...
Cependant, j'ai pu étudier avec une simulation informatique (car je ne l'ai pas eu en mains) un oculaire conçu par Donald C. Dilworth en 1988 (USA Patent N°4720183). Les qualités de cet oculaire à grand champ m'ont étonné et je vous le présente pour conclure cette revue des oculaires.
Quatre verres différents sont nécessaires pour réaliser ses huit lentilles.

La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
La lentille de champ disposée avant le foyer en fait un oculaire négatif, on ne peut donc pas envisager de l'équiper d'un réticule.
Le dégagement de son cercle oculaire est confortable mais il n'est pas compatible avec le port des lunettes.
Il a été conçu pour un champ visuel de 90°.
Cet oculaire forme des images plus fines que les Nagler ou l'Ethos et il supporte mieux les objectifs de grande ouverture (petits rapports F/D).
Comme le Nagler 1, il souffre d'une forte aberration de sphéricité sur sa pupille de sortie. Cela a pour conséquence un agrandissement "très important" de sa pupille de sortie, il ne faut donc pas l'employer pour les faibles grossissements surtout quand le rapport F/D est petit.
On peut lui faire la même remarque en ce qui concerne la difficulté de centrer l'objet observé mais cela ne devrait pas nuire à la qualité des images puisqu'elles sont bonnes sur tout le champ.
Autres caractéristiques des oculaires
Il faut maintenant évoquer la qualité de fabrication des oculaires.
Il y a tout d'abord le traitement antireflet qui influence le résultat surtout pour les oculaires qui ont de nombreuses lentilles.
Quand elle traverse un dioptre et indépendamment du phénomène de réfraction, la lumière subit une réflexion partielle. C'est la réflexion vitreuse dont la proportion est déterminée par l'expression suivante :
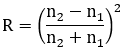
n1 et n2 représentent les indices de réfractions des deux milieux qui sont séparés par le dioptre considéré.
Cette relation nous indique que 4% de la lumière incidente est réfléchie au passage d'un dioptre air-verre ou verre-air (l'indice de réfraction du verre est environ égal à 1,5). Ainsi, une lentille avec ses deux faces provoque la perte par réflexion vitreuse de 8% de la lumière incidente. Cette proportion passe à 15% pour un oculaire à deux lentilles ou deux groupes de lentilles accolées (Huygens, Ramsden, Plössl...). Pour un Nagler 1 qui possède 8 surfaces air-verre, la réflexion vitreuse concerne 28% du flux lumineux incident.
La lumière ainsi réfléchie n'est pas simplement perdue, elle peut à nouveau être renvoyée vers la sortie de l'instrument par une autre réflexion vitreuse. Par conséquent, les réflexions internes entre les faces des différentes lentilles d'un oculaire provoquent une perte de contraste sur l'image finale ou peuvent même faire apparaître des images fantômes, c'est à dire des images qui ne correspondent à aucun objet existant dans le champ de vision de l'instrument.
Avec un traitement antireflet simple, l'amplitude de la réflexion vitreuse est divisée par 4 environ. Avec un traitement antireflet multicouche on peut la diviser par 40 environ.
On comprend donc que la qualité d'un oculaire qui comprend de nombreuses lentilles dépend des performances du traitement antireflet qui a été appliqué sur ses lentilles.
Il faut aussi parler de la qualité de fabrication proprement dite. Cela concerne le respect des côtes de fabrication (rayons de courbure et distances), la coaxialité des faces des lentilles, le centrage des lentilles, la qualité de leur polissage (j'ai déjà eu en mains des oculaires du commerce dont le polissage des lentilles n'était pas terminé!) ainsi que la qualité de l'usinage des parties métalliques. C'est généralement à l'usage qu'on pourra juger ces qualités. Toutefois, il est facile de constater les éventuels défauts de polissage. Il suffit d'observer une petite source lumineuse distante avec l'oculaire tout seul. En procédant ainsi, le champ de l'oculaire est uniformément éclairé et montre les moindres poussières présentes ou les piqures d'une lentille mal polie.
Pour favoriser le contraste, le constructeur devrait noircir le bord des lentilles. En effet, la partie extérieure de la lentille présente une surface dépolie, rugueuse et blanche qui ne demande qu'à réfléchir les éventuels rayons de lumière parasite... à moins qu'elle soit peinte en noir.
Fabrication d'un oculaire par un amateur
La fabrication d'un oculaire simple (Huygens, Dollond ou Ramsden) ne présente aucune difficulté pour un amateur qui a déjà réalisé un miroir puisqu'on peut tailler les lentilles dans du simple verre à vitre. Didier Godillon expose cette réalisation en détails dans son livre "Le guide de l'astronome amateur" et j'ai décrit succinctement cette méthode dans la page consacrée aux correcteurs de champ. Pour les petites lentilles, je remplace l'outil en verre par un bassinet en cuivre ou en laiton.

Observation photographique
Nous allons étudier ici des dispositifs qui complètent les télescopes ou les lunettes dans le but d'obtenir des images (réelles) plus grandes. Ils sont très utiles notamment pour la photographie à haute résolution car l'image formée au foyer de l'instrument est souvent trop petite pour que le capteur d'image puisse profiter de tout le pouvoir de résolution de l'objectif.
On peut considérer que ces systèmes allongent la distance focale de l'objectif sur lequel on les adapte. On parle alors de la distance focale résultante.
La disposition de certains des paragraphes suivants dans ce chapitre est certainement discutable car il y a des dispositifs parmi ceux que nous allons examiner qui sont souvent utilisés pour l'observation visuelle en complément des oculaires.
Pour la photographie astronomique des objets faibles ou étendus, on se contente souvent de la distance focale de l'instrument d'observation et on capture l'image formée au foyer (primaire ou secondaire). Pour cela, il faut disposer le capteur d'image sur le plan focal.
L'image peut être recueillie par un dispositif spécialisé comme une caméra électronique ou par un appareil photo numérique (APN) du commerce. Dans tous les cas, il faut que l'image puisse atteindre la surface sensible sans obstacle hormis l'obturateur et des filtres éventuels. Si nous voulons employer un APN, cela signifie qu'il faut lui ôter l'objectif, ce doit donc être un appareil "reflex".
Photographie avec objectif de l'APN
Lors des séances d'observation publique, il arrive fréquemment qu'une personne veuille photographier ce qu'elle voit dans l'oculaire avec son APN en mettant l'objectif de celui-ci derrière l'oculaire à la place de l'il. Quand je tente d'expliquer que le procédé n'est pas approprié, je vois systématiquement un regard plein de reproches se tourner vers moi...
Et je n'ose pas vous évoquer le dialogue qui arrive juste ensuite au sujet de l'utilisation du flash...
Par ailleurs, il est évident que la plupart des amateurs qui veulent réaliser leurs premiers clichés astronomiques vont tout d'abord être tentés d'employer leur APN avec lequel ils ont déjà réussi à immortaliser les images de superbes paysages ou de mémorables réunions de famille. Bien souvent l'objectif de cet APN n'est pas amovible.
Il me semble donc utile de disserter rapidement sur la photographie des images télescopiques avec un ANP équipé de son objectif. C'est un sujet que la plupart des auteurs évitent comme la peste... je comprends pourquoi.
La figure suivante nous permet d'analyser la configuration optique de ce procédé. Pour que la luminosité de l'image soit normale, il faut que la pupille de sortie de l'instrument d'observation soit positionnée dans le plan du diaphragme de l'objectif de l'APN. C'est rarement possible car dans les cas usuels, ce plan se trouve trop profondément enfoui dans l'objectif.

Il faudrait que le diaphragme de l'APN soit ouvert au maximum et encore cela ne suffira pas comme nous le voyons sur le graphique. Les rayons centraux parviennent jusqu'au capteur mais à partir d'une certaine distance de l'axe, variable selon la configuration, le parcours de la lumière est progressivement interrompu par le diaphragme de l'objectif.
Si la pupille oculaire était correctement placée, la luminosité de l'image sur le capteur serait uniforme. Dans notre cas, seule la partie centrale de l'image parvient correctement à l'objectif.
Pour la photographie d'une planète et à condition de bien la centrer dans le champ, on pourrait éventuellement se contenter de ce résultat. C'est alors qu'interviennent les autres difficultés :
- - Il faut pouvoir régler le temps de pose sur l'APN, c'est rarement possible quand il n'est pas reflex.
- Le temps de pose pour la photo d'une planète peut être de plusieurs secondes, il n'est pas possible de tenir l'appareil à la main dans ce cas.
- Pour maitriser la netteté de l'image, il faut bloquer le système de mise au point automatique de l'APN, ce n'est pas toujours possible.
- Pour maitriser la luminosité de la photo, il est nécessaire de bloquer l'automatisme qui gère le temps de pose et l'ouverture du diaphragme sur l'APN, ce n'est pas toujours possible. C'est pourtant nécessaire car ce système n'est vraiment pas adapté à la prise de clichés astronomiques.
- Il faut arrêter le flash (je ne suis pas certain que ce soit toujours possible).
Selon ce montage, avec un oculaire de distance focale "f" et un objectif de l'APN dont la distance focale est "F", l'image télescopique est agrandie dans le rapport G :

Toutefois, cette relation est inutile quand on ne connaît pas la distance focale "réelle" de l'objectif de l'APN or c'est la distance focale "équivalente" qui est habituellement indiquée.
Avec cette méthode, les seules fois où j'ai pu constater un résultat "regardable", cela concernait des images de la Lune ou du Soleil et l'image assombrie sur ses bords n'occupait que le centre du cliché.
La lentille de Barlow est un dispositif optique divergent imaginé par Peter Barlow (Physicien anglais né le 13 octobre 1776 à Norwich et mort le 1er mars 1862 à Woolwich) qui allonge la distance focale de l'objectif. En fait, elle est couramment composée par un doublet (2 lentilles) et parfois par un triplet (groupe de 3 lentilles).
Elle est principalement caractérisée par sa distance focale qui est négative et par le grandissement pour lequel elle a été conçue. On dégrade la qualité des images si on l'emploie pour un grandissement différent.

F est le foyer de l'objectif
Fr est le foyer résultant
Grandissement = G

avec : f = valeur absolue de la distance focale de la lentille de Barlow
Tirage = E

Une lentille de Barlow permet d'allonger la distance focale d'un instrument sans modifier son encombrement. Ainsi, selon qu'on l'utilise avec ou sans Barlow, un jeu d'oculaire pourra fournir deux ensembles de grossissements différents.
Un télescope ouvert à F/6 sur lequel on a monté une lentille de Barlow de grandissement égal à 2 aura une distance focale résultante doublée et son rapport d'ouverture résultant deviendra F/D=12.
Les modèles les plus ordinaires sont constitués par une lentille unique qui possède une superbe aberration chromatique. Il faut absolument les éviter.
L'opticien qui conçoit une Barlow achromatique (2 lentilles) ou apochromatique (3 lentilles) dispose de certaines libertés sur le choix des courbures des lentilles et de la nature des verres. Il peut les mettre à profit pour corriger des aberrations telles que la coma ou l'astigmatisme afin d'obtenir des images nettes loin de l'axe, la Barlow devient ainsi un correcteur de champ.
On trouve sur le marché un grand choix de lentilles de Barlow qui différent par leurs caractéristiques optiques, leurs diamètres, leur domaine spectral, les caractéristiques de leur traitement antireflet, la qualité de leur fabrication...
Généralement, les lentilles de Barlow employées par les astronomes amateurs ont une distance focale comprise entre 50 et 220mm, un diamètre entre 25 et 50mm et un grandissement entre 1,5 et 2,5 fois. Elles sont montées dans un tube que l'on doit disposer dans le porte-oculaire. Pour l'observation visuelle, on introduit un oculaire dans l'autre extrémité de ce tube. On trouve le même choix de coulants que pour les oculaires.
Pour la photographie, il suffit de disposer le capteur d'image au niveau du plan focal résultant. Dans ce cas, le tube qui contient la Barlow peut être gênant s'il est trop long.
Dans un article de mai 1935 paru dans la "Revue d'Optique" et intitulé "Systèmes correcteurs pour réflecteurs astronomiques", Maurice PAUL (concepteur opticien français 1890-1981) définit théoriquement un doublet de Barlow aplanétique du type Clairaut. Le terme "aplanétique" explique que ce dispositif corrige la coma et le "type Clairaut" indique que les deux lentilles sont collées.
La revue "L'Astronomie" de la Société Astronomique de France dans son numéro de Mai 1955 présente un article de sa commission des instruments dans lequel on apprend que la formule de lentille de Barlow de 2x calculée par Maurice Paul est retenue par les établissements Clavé pour être fabriquée et commercialisée.
J'ai employé cette lentille de Barlow pendant des années et je connais bien ses limitations.
Je l'illustre sur la figure suivante en reprenant la présentation employée plus haut pour les oculaires. Il y a un changement cependant car le graphique qui représente la plus grande dimension des images stellaires en fonction de la distance à l'axe est maintenant exprimé avec des unités linéaires (et non plus angulaires).
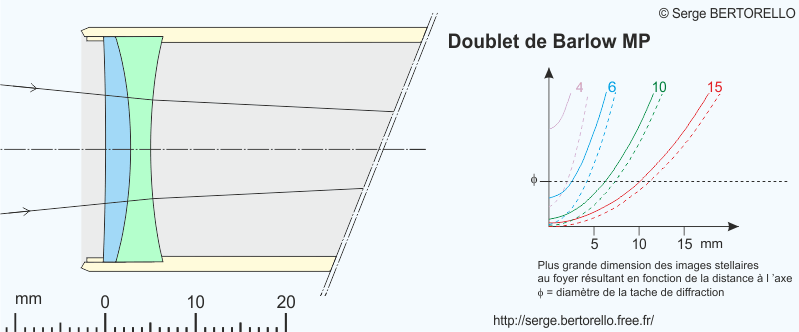
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.
Comme pour les caractéristiques des oculaires, les courbes sont réalisées pour différents rapports d'ouverture. On constate que plus celui-ci est petit et moins la Barlow est performante.
Cette lentille de Barlow a été calculée pour fournir une image sans coma. Cette qualité serait très appréciable sur un télescope si elle ne présentait pas un astigmatisme important.
Avec mes télescopes ouverts à F/D=5, le champ photographiable avec netteté en employant cette Barlow est plus petit que la dimension apparente de la Lune ou du Soleil. De plus, un spectre secondaire est visible lors des observations visuelles.
Pour un rapport F/D égal ou supérieur à 6, nous pouvons employer cette lentille de Barlow pour doubler le grossissement obtenu avec notre jeu d'oculaires. Par contre, avec un rapport F/D inférieur, elle dégrade trop la qualité des images obtenues avec des bons oculaires.
Le doublet de Barlow suivant a été conçu pour minimiser l'ensemble des aberrations sans annuler aucune.
Ce dernier modèle possède un champ plus étendu mais il n'est pas mieux adapté aux petits rapports F/D.
Je pense qu'on ne peut pas obtenir de bien meilleures caractéristiques avec un doublet.
En avançant ou en reculant la lentille de Barlow, on peut modifier le grandissement qu'elle procure en s'inspirant des formules données plus haut. Cela ne s'obtient pas sans perte de qualité.
Pour un rapport F/D égal ou supérieur à 10, cette dégradation est supportable. Par contre avec les grandes ouvertures, il ne faut pas s'éloigner du rapport de grandissement indiqué par le constructeur sous peine d'obtenir des images fortement dégradées.
Note sur l'aberration chromatique des lentilles de Barlow : Mes remarques sur l'aberration chromatique des lentilles de Barlow et mes graphiques se rapportent aux observations visuelles. Cette aberration est aggravée lors de l'emploi de capteurs d'images qui possèdent une sensibilité spectrale plus étendue que l'il humain (caméra CCD par exemple).
On ne peut pas choisir une Barlow sur catalogue. La seule méthode pour faire un bon choix consiste à essayer différents modèles sur le télescope considéré. C'est un des avantages de faire partie d'un groupe d'observateurs. On peut aussi profiter d'un rassemblement d'astronomes amateurs.
Le résultat est surprenant : les doublets ou triplets de Barlow ne supportent pas les grandes ouvertures.
Ne vous laissez pas influencer par le témoignage d'un utilisateur qui n'a pas le même type d'instrument que vous (surtout si le rapport d'ouverture est différent). Ne vous laissez pas non plus influencer par un article de presse qui vante les qualités d'une Barlow sans préciser l'ouverture de l'instrument sur lequel a été fait le test.
Selon que vous souhaitez faire une observation visuelle ou photographique, votre choix pourra être différent. En effet, pour une observation visuelle, vous chercherez à obtenir les images les plus fines au centre du champ alors que pour photographier une nébuleuse étendue vous serez moins difficile sur la finesse mais vous voudrez exploiter un champ plus grand.
Par ailleurs, l'emploi d'une lentille de Barlow avec une caméra électronique doit se faire avec un filtrage bien étudié. En effet, ces capteurs ont une sensibilité spectrale qui s'étend dans l'infrarouge et les doublets ou triplets de Barlow n'ont pas été prévus pour cela.
Pour amplifier encore le grandissement de l'image focale, on peut employer une deuxième Barlow sur le foyer résultant obtenu avec une première lentille de ce type.
Si chacune de ces Barlow est utilisée avec son grandissement théorique, cette association de deux lentilles fonctionne sans détérioration supplémentaire de l'image. Je dois toutefois préciser que j'ai étudié seulement des associations de Barlow identiques.
Ainsi, en associant deux Barlow 2x, on obtient une distance focale résultante 4 fois plus longue.
Lentille de Barlow et télescope très ouvert
La course aux gros diamètres et le besoin de transporter son télescope contribuent au succès actuel des instruments très ouverts. On rencontre de plus en plus des télescopes dont le rapport F/D est inférieur à 5, voire même inférieur à 4.
Les lentilles de Barlow classiques, qu'elles soient constituées par un doublet ou un triplet, donnent de mauvaises images avec ces instruments même au centre du champ.
Les agrandisseurs télécentriques
Les établissements qui vendent des accessoires pour l'observation astronomique proposent parfois sous l'appellation "lentille de Barlow" des dispositifs qui ne répondent pourtant pas à la définition.
Je pense notamment à la série Powermate de la marque Televue. Ces dispositifs agrandisseurs sont composés d'un doublet divergent suivi d'un doublet convergent espacés de quelques centimètres. Ce ne sont donc pas des lentilles de Barlow bien que certains les nomment "Barlow télécentriques".
J'utilise un Powermate 2,5x qui me donne satisfaction autant pour les observations visuelles que photographiques avec mes télescopes ouverts à F/5 (mais je ne connais pas ses caractéristiques de fabrication).
Je vous propose d'étudier le principe des agrandisseurs télécentriques en examinant la figure suivante.
Observons tout d'abord l'image de gauche qui représente l'emploi d'une lentille de Barlow. Elle nous permet de constater que le faisceau qui forme un point de l'image est d'autant plus incliné qu'il est éloigné de l'axe optique. Les axes des différents faisceaux lumineux semblent provenir d'un point O proche du dispositif et dont la position ne varie que très légèrement en fonction de la distance focale de l'objectif.
On peut dire aussi que dans ce cas les faisceaux hors de l'axe sont beaucoup plus inclinés qu'ils ne le seraient avec un objectif de longue focale employé sans la Barlow.
Sur l'image de droite, pour constituer un agrandisseur télécentrique, nous avons disposé après la Barlow une lentille convergente dont le foyer objet est placé précisément au point O. Ainsi l'axe de chaque faisceau lumineux arrive sur l'image tout en étant parallèle à l'axe optique. Autrement dit, les axes de ces faisceaux ne sont plus inclinés et le centre optique de l'objectif semble être repoussé à l'infini.
Cet aspect favorise l'utilisation d'un oculaire que l'on emploierait pour examiner l'image obtenue avec l'amplificateur.
Notons en passant que cette propriété est très appréciable quand on dispose un filtre interférentiel juste avant le foyer. Ceci est notable car les fréquences passantes au travers de ces filtres varient en fonction de l'inclinaison de la lumière incidente.
On constate aussi que, en reculant l'image (en augmentant la distance t) on ne modifie pas sa taille comme cela se produit avec une Barlow.
Certains auteurs soulignent que l'emploi de la Barlow défavorise la luminosité de l'extrême bord des images observées avec un oculaire car l'inclinaison des rayons du bord les oriente hors des lentilles de l'oculaire. La figure 19 illustre ce phénomène en le comparant avec l'emploi d'un amplificateur télécentrique.
En pratique, pour constater cette perte de champ, il faut employer une barlow "compacte" (c'est à dire qu'elle doit avoir une petite distance focale) avec un oculaire de grande distance focale. J'ai rencontré ce problème en testant une "Barlow Celestron 2x Ultima SV series" sur mon télescope SIRIUS (D = 256 mm, F/D = 4,64). En l'employant avec mes oculaires Clavé de 20mm et plus, le bord de l'image est nettement absent, on ne voit plus le diaphragme de champ.
Quoi qu'il en soit, l'utilisation d'un amplificateur télécentrique favorise un bon fonctionnement des oculaires. La figure suivante montre un exemple d'amplificateur télécentrique.
Lorsqu'un oculaire fournit une image nette en observation visuelle, les rayons correspondants aux différents points de l'image sont parallèles entre-eux. On dit que l'image est formée à l'infini.
Si nous reculons légèrement l'oculaire, nous l'éloignons un peu du foyer de l'objectif et, dans ces conditions, l'image qu'il forme se rapproche et peut être reçue sur un écran ou sur une surface sensible (film photo, capteur CCD,...).
La figure suivante montre cette méthode de projection en assimilant l'oculaire à une lentille mince. Elle est semblable à la figure 2 de la page sur le calcul des combinaisons optiques qui nous a permis de présenter les formules de Descartes.
L'image objet AB appartient à l'image focale fournie par l'objectif. Elle est agrandie par l'oculaire en une image A'B'.
Pour déterminer ce montage, nous pouvons employer la première formule de Descartes :
avec : p = distance entre l'objet et la lentille
Puis la deuxième formule de Descartes :
g est le grandissement.
Toutefois, on pourrait penser que, hormis celui de Kepler, un oculaire ne peut jamais être considéré comme une lentille simple. La situation doit être plus complexe comme le montre la figure 22.
Vous pouvez voir sur cette image que la configuration optique de ce système est éloignée de la situation de la lentille mince pour laquelle nous avons employé les formules de Descartes. Pourtant, même ici, ces formules fournissent un résultat proche de la réalité.
La figure 22 montre aussi pour deux grandissements différents (5x et 10x) avec un oculaire de Plössl les courbes caractéristiques de la finesse des images en fonction de la distance à l'axe au niveau du foyer résultant. Comme pour les graphiques précédents, le nombre correspondant à chaque courbe correspond à la fois au rapport F/D de l'instrument considéré et à la distance focale de l'oculaire en millimètres.
Vous comprenez la difficulté rencontrée pour faire une photo planétaire en employant cette méthode de projection avec un objectif ouvert à F/4 et un oculaire de Plössl de 4mm. On ne pourra obtenir la résolution théorique qu'au centre du cliché. On pourrait améliorer la situation en employant un bon oculaire de plus courte focale ce qui est rare car difficile à réaliser avec la précision nécessaire.
En maintenant un écran transparent derrière l'oculaire d'un télescope, on peut projeter sur celui-ci l'image du Soleil pour l'observer en toute sécurité sans employer de filtre. Cela permet de présenter l'image du Soleil à tout un groupe de personnes sans leur imposer de faire la queue pour que chacun attende son tour. Chaque membre du public présent peut même photographier sans difficulté et sans risque le disque solaire avec son appareil photo ordinaire.
Pour réaliser cet écran de projection, j'emploie une feuille de plastique destinée à être utilisée comme papier calque par les dessinateurs industriels. Le grain de ce matériau est très fin, je considère qu'il convient très bien à cet usage.
Depuis mes débuts dans l'astronomie amateur, j'ai toujours lu les mêmes exposés sur les oculaires, les différents auteurs ne faisaient preuve d'aucune originalité sur ce sujet et se recopiaient les uns les autres au mot près. Cela signifie que la technique du Copier-Coller était déjà d'un emploi courant bien avant l'avènement de la micro-informatique.
Il faut bien être conscient que les versions initiales de ces commentaires avaient été rédigées à une époque où le rapport d'ouverture le plus courant était F/D=15. Vous comprendrez donc que ces textes sont complètement inadaptés aux instruments très ouverts qui sont communs aujourd'hui.
Quelqu'un a dit "le plus mauvais élément d'un instrument est l'atmosphère". Oui, j'en suis convaincu si cet appareil est bien conçu et bien employé. Cependant, s'il s'agit d'un télescope ouvert à F/D=4 (ou moins)... vous savez maintenant, qu'il faut l'équiper d'un oculaire soigneusement choisi car sinon cet accessoire risque de ravir la première place à notre atmosphère dans la liste des causes de mauvaises images.
Par ailleurs, l'astrophotographie à haute résolution a pour but de révéler les plus fins détails que peut fournir théoriquement un instrument d'observation. Maintenant, vous savez pourquoi certains amateurs n'arrivent pas à atteindre ce but malgré des efforts louables. Le manque de netteté de leurs clichés peut être causé par un mauvais choix de leur dispositif grandissant ou un mauvais usage de celui-ci.
Je souhaite que cet exposé vous permette d'améliorer la finesse de vos observations.

Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.




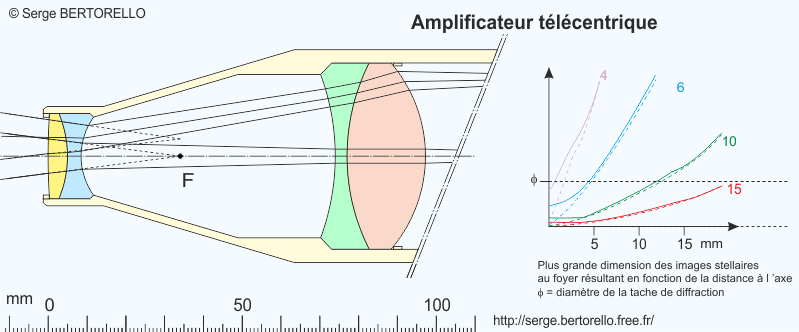
La lumière vient de l'objectif situé à gauche de la figure.
Cliquer sur l'image pour obtenir les caractéristiques de fabrication.
Graphiques réalisés à l'aide du logiciel CORRECT 3.


p' = distance entre la lentille et l'image
f ' = 0F' = distance focale de la lentille


Les graphiques indiquent la plus grande dimension des images stellaires au foyer résultant pour 2 grandissements (5x et 10x).
Graphiques réalisés à l'aide du logiciel CORRECT 3.

Je présente sur une autre page cette séance d'observation du transit de Vénus en expliquant pourquoi il est normal que le Soleil n'est pas parfaitement circulaire ici.
Conclusion

