Les correcteurs de champ
Les instruments qui forment l'image d'un objet fournissent des fins détails au centre du champ observé. Toutefois, la qualité se dégrade, parfois très vite, quand on s'éloigne de l'axe à cause de la coma ou de l'astigmatisme, ce sont des défauts que les opticiens appellent aberrations. C'est pour les corriger que l'on utilise les correcteurs de champ.
Avant l'avènement de la photographie, peu de gens se préoccupaient des aberrations extra-axiales des instruments d'observation astronomiques. Mais après que l'on eut pris les premiers clichés du ciel, les théoriciens de l'optique furent sollicités pour concevoir des instruments à grand champ. Dans les premières années du vingtième siècle, l'astronome et physicien allemand Karl SCHWARZSCHILD (1873 - 1916) jeta les bases du calcul des aberrations des instruments optiques. Ses théories lui permirent d'obtenir la formule d'un télescope possédant des aberrations extrêmement réduites : Le télescope de Schwarzschild. Toutefois, cette configuration avait des inconvénients qui ont entravé son développement. Plus tard, le célèbre opticien-inventeur français Henri CHRETIEN (1er février 1879 - 6 février 1956) inventa un télescope à faibles aberrations dont l'américain George Willis RITCHEY (31 décembre 1864 - 4 novembre 1945) construisit le premier exemplaire. Cette formule, connue sous le nom de télescope de RITCHEY-CHRETIEN, théoriquement moins parfaite que celle de SCHWARZSCHILD, eut beaucoup de succès et a été adoptée pour de nombreux instruments. Cependant cette combinaison est peu favorable aux grandes ouvertures (petits rapports F/D). Un autre problème est posé par les télescopes de SCHMIDT qui fournissent de merveilleuses photographies à grand champ avec de grandes ouvertures, mais qui ne peuvent pas être utilisés pour l'observation visuelle.
De nombreux astronomes souhaitent un télescope universel. Cet instrument permettrait de faire des photographies à grand champ avec une grande ouverture, il pourrait être utilisé pour les observations planétaires avec le pouvoir de résolution théorique et accepterait les observations visuelles. Il serait peu encombrant et aisé à fabriquer et à régler. Pour l'instant, cet instrument est utopique mais il est possible de s'approcher de sa définition.
Le problème de l'universalité des télescopes se pose chaque fois que l'on conçoit un instrument de gros diamètre, celui-ci doit pouvoir être utilisé pour des travaux très divers. Ainsi, l'étude de faisabilité d'un télescope de 5 mètres qui précéda la mise en chantier de l'observatoire du Mont Palomar a stimulé ces études. Il apparut très vite qu'une combinaison de SCHWARZSCHILD nécessiterait une coupole trop importante et trop onéreuse. La formule de CHRETIEN ne permettait pas les très courts foyers, or le rapport d'ouverture souhaité était F/D = 3,3. Avec cette ouverture, pour une résolution de 1" (une seconde d'arc), le champ d'un télescope de NEWTON a 2' (deux minutes d'arc) de diamètre !
Pour agrandir le champ photographiable, Franck E. ROSS proposa en 1935 une solution originale. Il s'agit d'un dispositif correcteur de champ constitué par deux lentilles à faces sphériques qui se placent un peu en avant du foyer. Ce correcteur de champ est facile à construire et à utiliser. Toutefois, il faut savoir que le télescope qui en est équipé hérite d'une aberration de sphéricité. Cette dernière peut être éliminée en donnant à la méridienne du miroir principal une forme hyperbolique (coefficient de déformation < -1). Or ce correcteur est habituellement utilisé sur des télescopes à miroir parabolique, il faut donc ôter le correcteur de champ pour les observations visuelles. L'opticien choisit les caractéristiques pour que le champ utilisable soit le plus grand possible sans que l'aberration de sphéricité soit sensible.
Un télescope de NEWTON peut donc posséder un champ relativement étendu avec une ouverture importante s'il est équipé d'un correcteur de ROSS. Pour les observations visuelles et les photographies à haute résolution, il faut ôter ce correcteur.
Depuis, de nombreuses formules de correcteurs de champ ont été inventées. Elles se distinguent par leurs caractéristiques optiques ainsi que par le nombre, la taille et la forme de leurs lentilles. Ainsi, un autre dispositif a été calculé par Franck E. ROSS. Ce correcteur de ROSS à trois lentilles a été utilisé sur quelques grands télescopes jusqu'aux années soixante.
A partir de 1967, C. G. WYNNE, a indiqué des formules de correcteurs de champ composées de trois et quatre lentilles. Ceux-ci, ne laissent pas d'aberration de sphéricité résiduelle, mais ils sont encombrants.

Si les instruments d'observation étaient idéalement parfaits, ils fourniraient des images infiniment détaillées. En les agrandissant, on obtiendrait toujours plus de détails.
En fait, la nature ondulatoire de la lumière impose une limite à la finesse des détails fournis par un objectif. A cause des phénomènes de diffraction, l'image d'un point lumineux est étalée sur une tache ronde. C'est le disque d'Airy qui est entouré d'anneaux concentriques faiblement lumineux. La figure 1 montre l'image d'une étoile fournie par un bon télescope. Dans le cas le plus favorable, on peut apercevoir les 2 premiers anneaux, les suivants sont trop faibles pour être vus. Un objectif parfait ne donne donc jamais comme image une réplique parfaite de l'objet, mais un ensemble de disques d'Airy juxtaposés. Le disque d'Airy constitue la limite des plus fins détails que peut fournir un objectif (voir sur une autre page de ce site "la diffraction dans un faisceau limité par une ouverture circulaire").
Le rayon du disque d'Airy est ρ (lettre grecque "rho") :
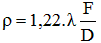
Avec : λ = longueur d'onde de la lumière
F = distance focale de l'objectif
D = diamètre de l'objectif
On parle d'aberration quand les rayons lumineux sont dirigés à l'extérieur de la tache d'Airy. Nous examinerons ici les défauts des images dus à la conception des instruments et non pas les défauts de fabrication.
On classe ces imperfections parmi six aberrations fondamentales. Il s'agit de l'aberration chromatique et des cinq aberrations géométriques élémentaires du troisième ordre. Cette dernière expression désigne le niveau d'approximation des calculs.
J'ai disposé une présentation détaillée de ces aberrations ici et là mais voici un rappel.
Elle caractérise uniquement les dispositifs composés de lentilles et ne concerne pas les systèmes à miroirs.
Le pouvoir de réfraction d'un verre varie en fonction de la longueur d'onde de la lumière. Autrement dit, les propriétés optiques d'une lentille dépendent de la couleur de la lumière qui la traverse. Or la lumière qui nous provient des astres est composée de rayons de différentes couleurs. Quand un instrument optique superpose mal les représentations de l'objet observé dans ces différentes couleurs, on dit qu'il souffre d'une aberration chromatique. Pour un instrument donné, l'aberration chromatique n'est pas la même suivant qu'il est utilisé pour la vision, pour la photographie, pour un capteur CCD, etc. Il faut donc définir le domaine spectral que l'on considère. Si cette aberration est corrigée, on dit que l'optique est achromatique.

On parle de cette aberration quand les rayons lumineux qui passent par le bord de l'objectif forment une image en avant ou en arrière de celle qui est composée par les rayons proches de l'axe. Les rayons centraux et les rayons marginaux ne convergent pas à la même distance de l'objectif (figure 2).
L'image résultante est également floue au bord et au centre du champ.
Dans la formulation mathématique qui caractérise les aberrations d'un système optique, l'aberration de sphéricité est constituée par les termes qui sont indépendants de la distance à l'axe.

La figure 3 montre l'image d'une étoile fournie par un télescope de NEWTON en dehors de l'axe optique. Cette aigrette, appelée la coma, s'agrandit quand on s'écarte du centre du champ. C'est surtout elle qui limite l'étendue du champ exploitable en photographie avec un tel télescope.
La longueur de cette aigrette est proportionnelle à la distance à l'axe. La formule suivante donne sa valeur sur un télescope de NEWTON :

Avec : D = diamètre du miroir primaire
F = distance focale
α = distance à l'axe
Cette formule est aussi valable pour la combinaison de CASSEGRAIN. Dans ce cas, il suffit de donner à F la valeur de la distance focale résultante.
Considérons le grand télescope de NEWTON du mont Palomar. Son miroir a un diamètre de 5,08m et sa distance focale vaut 16,3m. Pour ce prestigieux instrument, la formule précédente nous indique :
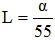
A 55" de l'axe de ce télescope la coma a déjà une longueur de 1". Ainsi, pour un pouvoir de résolution de 1" le champ exploitable au foyer de l'instrument aura seulement 9mm de diamètre. De plus, il faut particulièrement soigner le centrage de l'image si on veut prendre un cliché de Jupiter (diamètre 40") avec une résolution de 0,5".

Vous pouvez voir ci-dessus un cliché de M33 pris au foyer du télescope ALCOR de 256mm de diamètre et de 1187mm de distance focale (F/D= 4,6). C'est une pose de 45mn sur TP2415 hypersensibilisé. Il ne représente qu'une partie du cliché de 24x36mm et pourtant la coma est déjà sensible sur les étoiles situées sur le bord de l'image de la galaxie.
On dit qu'un instrument est aplanétique quand il est corrigé simultanément de l'aberration de sphéricité et de la coma.
L'astigmatisme et la courbure de champ :
Lorsqu'on s'écarte beaucoup de l'axe d'un système aplanétique on constate un étirement des images d'étoiles qui peuvent prendre la forme d'un trait. Il s'agit de l'astigmatisme. Notez que l'on désigne aussi sous ce terme des imperfections de fabrication que nous ne considérons pas ici.
D'autre part l'image semble être projetée sur une surface courbe et non pas sur un plan. C'est la courbure de champ.
Ces deux aberrations provoquent des défauts de l'image proportionnellement au diamètre de l'optique et, en première approximation, au carré de la distance à l'axe. L'astigmatisme est beaucoup moins sensible que la coma sur les télescopes usuels. Il faut toutefois remarquer que son effet est bien plus important sur un télescope de CASSEGRAIN que sur un NEWTON d'ouverture équivalente.
Une image peut être nette en tous points et être déformée, on dit qu'elle a une distorsion. Cette aberration est indépendante de l'ouverture de l'instrument. Elle correspond au fait que le grossissement ou le grandissement d'une image n'est pas le même au centre et au bord du champ. Sur un cliché astronomique, elle n'est préoccupante que si l'on veut mesurer la position des objets (astrométrie).
Avant que l'on ait pu imaginer des méthodes pour corriger ces aberrations, les constructeurs d'instruments avaient compris qu'ils pouvaient atténuer les effets en choisissant de grandes distances focales. Ils ont conçu ces "longues lunettes à faire peur aux gens" (selon l'expression de Molière <1622-1673> dans sa pièce "Les Femmes savantes" de 1672). En 1733, Chester Moor Hall découvrit la possibilité de corriger les objectifs des lunettes de l'aberration chromatique. Les autres aberrations ont été tout d'abord corrigées ou atténuées d'une façon empirique qui était personnelle à chaque constructeur. Maintenant ce problème est résolu par le calcul.
Un objectif de lunette est composé par deux lentilles. On détermine la puissance de chacune d'elles en fonction de la longueur focale souhaitée et des propriétés des verres employés afin d'obtenir une combinaison achromatique. A partir de là, l'opticien peut encore jouer sur la forme des lentilles (la cambrure) pour corriger les autres aberrations. L'objectif couramment utilisé en astronomie pour les observations visuelles est un doublet achromatique et aplanétique dont la formule est désormais classique.
De même on peut corriger les aberrations sur les télescopes à deux miroirs. Nous ne considérons pas sous cette rubrique le télescope de NEWTON car son miroir plan est facultatif et ne sert qu'à la commodité de l'observation, il n'intervient pas dans le principe formateur des aberrations. Dans la combinaison de CASSEGRAIN, on peut modifier légèrement la forme des miroirs pour obtenir un télescope aplanétique de RITCHEY-CHRETIEN. En apparence, celui-ci ressemble à s'y méprendre à un CASSEGRAIN mais ses miroirs ont une méridienne hyperbolique. D'autres combinaisons de deux miroirs ont été conçues notamment par Karl SCHWARZSCHILD et André COUDER.
Parmi toutes ces formules à deux miroirs, c'est celle de RITCHEY-CHRETIEN qui est la plus appréciée. Elle a un champ relativement étendu qui n'est limité que par son astigmatisme mais elle est pratiquement absente du monde des astronomes amateurs.
Les astronomes amateurs qui construisent leur télescope réalisent surtout des télescopes de NEWTON. Avec une courte distance focale, cet appareil fournit à son foyer une image très lumineuse. Avec un dispositif agrandisseur utilisant une lentille de BARLOW ou un oculaire, il permet des clichés planétaires. Ajoutons à cela qu'il convient très bien pour les observations visuelles. Hélas, la coma restreint beaucoup la taille du champ utilisable mais on peut nettement agrandir ce dernier en utilisant un correcteur de champ.
Nous allons passer en revue quelques dispositifs qui agrandissent la taille du champ exploitable. Sauf indication contraire ces dispositifs sont destinés à un télescope de NEWTON.
Le système le plus simple pour corriger l'image au foyer d'un instrument d'observation consiste à diaphragmer son objectif, c'est à dire diminuer son diamètre. En procédant ainsi on diminue l'influence des aberrations ainsi que les performances de l'optique. Dans certains cas cela peut être profitable comme lorsqu'on veut photographier l'ensemble du disque du Soleil ou de la Lune et que les aberrations de l'objectif ne permettent pas une netteté suffisante sur toute l'image. Ce cliché ne nécessite pas la résolution maximale de l'objectif et on peut accepter une perte de luminosité.
Ce procédé est applicable à tout type d'objectif.
Le correcteur de ROSS à deux lentilles :

Franck E. ROSS a conçu un doublet de puissance nulle pour corriger les aberrations d'un télescope de NEWTON. Ce correcteur de champ est facile à construire et à utiliser. Il fournit un champ plan corrigé de la coma, avec un astigmatisme réduit de moitié. Toutefois, il faut savoir que le télescope de NEWTON qui en est équipé hérite d'une faible aberration de sphéricité.
Dans un article de mai 1935 paru dans la "Revue d'Optique" et intitulé "Systèmes correcteurs pour réflecteurs astronomiques", Maurice PAUL (concepteur opticien français 1890-1981) définit théoriquement ce correcteur. Il nous montre qu'il doit répondre aux deux équations suivantes :
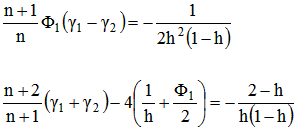
Avec : distance focale du miroir primaire = 1
n = indice de réfraction du verre constituant les 2 lentilles (réalisées dans le même matériau)
Φ1 = puissance de la première lentille
γ1 = cambrure de la première lentille
γ2 = cambrure de la deuxième lentille
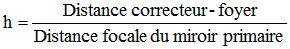
Pour h donné, γ1 et γ2 s'expriment en fonction du paramètre indépendant Φ1, puissance de la première lentille. En théorie, il y a donc une infinité de solutions. L'expérience nous montre que toutes ces solutions n'ont pas les mêmes performances. Il nous faut choisir la formule qui donne les moindres aberrations. Dans les cas habituels, l'expérience nous indique Φ1 = -5,4 pour n=1,52.
Les deux lentilles qui le composent sont réalisées dans le même verre et sa puissance globale est nulle, il est donc achromatique.
Le correcteur de ROSS à 2 lentilles introduit une aberration de sphéricité. La formule suivante indique le diamètre, en secondes d'arc, de la tâche d'aberration de sphéricité fournie par un tel correcteur installé sur un télescope à miroir parabolique :
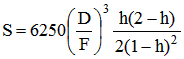
Nous en déduisons que l'aberration de sphéricité est faible pour les petites valeurs de h ou, si vous préférez, quand le correcteur est proche du foyer. Mais dans ce cas, le champ est faible. En concevant un tel correcteur, il faut donc rechercher le meilleur compromis entre l'étendue du champ exploitable et la finesse des images. Avec un miroir primaire parabolique ouvert à F/D=5 et une distance correcteur - foyer de 60mm, on obtient des images d'étoiles d'un diamètre inférieur à 30µm sur un champ de 30mm de diamètre. Sans ce dispositif, le diamètre du champ serait limité à 8mm. Il faut ôter ce correcteur pour les observations visuelles ou pour la photographie à haute résolution.
Notez que l'aberration de sphéricité peut être éliminée en donnant à la méridienne du miroir principal une forme hyperbolique (coefficient de déformation inférieur à -1).
A titre d'exemple, nous allons détailler les caractéristiques de construction d'un correcteur de ROSS à deux lentilles optimisé pour couvrir le champ d'un cliché 24x36 au foyer d'un télescope de NEWTON de 200mm de diamètre et 1m de distance focale.
Pour illustrer les performances des correcteurs présentés dans cet exposé, je propose sur la droite de chaque figure un graphique dont les courbes montrent la plus grande dimension des images stellaires en fonction de la distance à l'axe optique mesurée sur le plan focal résultant. Chacun de ces graphes est issu d'une simulation informatique.
Les instruments considérés ici sont des télescopes de Newton de 1m de distance focale.
La courbe en trait plein correspond à la plus grande dimension de l'image stellaire obtenue avec le correcteur en considérant le domaine spectral entre 404,7nm et 656nm. La courbe noire en pointillé est obtenue en considérant uniquement la longueur d'onde de 546nm qui correspond approximativement au maximum de la sensibilité spectrale de l'il humain. Quant à la courbe rouge en pointillé elle est obtenue avec le miroir parabolique seul, sans le correcteur.
Franck E. ROSS a défini d'autres types de correcteurs à 3 ou 4 lentilles.
En 1967, Charles G. WYNNE a décrit un correcteur de champ à quatre lentilles constituées du même verre (Applied Optics, N°6, 1967). Celui-ci fournit de très bonnes images sur les télescopes de NEWTON très ouverts. A partir de l'année suivante, il a régulièrement publié des formules à trois lentilles de performances similaires voire meilleures. Ces dernières étaient initialement destinées à être utilisées au foyer du miroir primaire des combinaisons de RITCHEY-CHRETIEN. En 1974, il a indiqué une combinaison à trois lentilles qui corrige les images d'un miroir parabolique ouvert à F/3 (Monthly Notices N°167, 1974).
Ces formules donnent des champs plans et bien corrigés. C'est surtout le modèle à trois lentilles qui est répandu auprès des grands télescopes. Globalement celui-ci est meilleur que son homologue à quatre lentilles.
Nous vous proposons ci-dessous une formule à trois lentilles destinée à équiper le miroir parabolique d'un télescope de Newton.
L'épaisseur totale entre le premier dioptre et le foyer résultant = 174,1mm. C'est énorme et on peut estimer qu'il est beaucoup trop gros pour le télescope de 200mm de diamètre et 1000mm de focale que nous utilisons comme référence... mais on peut employer avec bonheur cette formule avec un instrument plus gros tel qu'un T400 avec F=2000. En fait plus, la distance focale de l'instrument est grande (avec F/D ≥ 3) et meilleur sera le résultat.
Ce dispositif fait reculer le foyer de 13,28mm et allonge la distance focale de 11%. Quand on le monte sur le télescope de 200mm ouvert à F/5, l'image de diffraction n'est pas altérée jusqu'à plus de 10mm de l'axe (jusqu'à plus de 15mm de l'axe sur T400 F/D=5) et le champ peut être exploité pour la photographie au foyer jusqu'à plus de 23mm de l'axe.
Ce correcteur de Wynne fournit encore des résultats honorables avec un rapport F/D égal à 3.
Au vu de ces performances, n'allez pas imaginer qu'il est intéressant de l'utiliser pour l'observation visuelle en observant à l'oculaire l'image ainsi corrigée. En effet, les oculaires ont de telles aberrations en dehors de l'axe qu'on ne gagnerait pas grand-chose en pratiquant ainsi. De plus la dernière épaisseur est très petite. Elle correspond à la distance qui sépare le foyer final de la dernière lentille. De nombreux oculaires ont besoin d'un dégagement plus important.
Le correcteur de Wynne fournit de belles images mais il est très encombrant et son trop court dégagement du foyer peut contre-indiquer l'emploi de certains dispositifs de prise de vue tels que roue à filtres ou même APN (appareil photo numérique).
Pour accroître ce dégagement du foyer, il faut augmenter les dimensions du correcteur et elles deviennent vraiment rédhibitoires pour les instruments d'amateurs.
Un correcteur de champ à 4 lentilles :
Le correcteur de Wynne est encombrant et il a un dégagement trop faible (espace entre la dernière lentille et l'image) qui ne permet pas de l'employer avec la plupart des oculaires ni même de disposer un accessoire tel qu'une roue à filtres devant le capteur d'image.
C'est pour palier à ces inconvénients qu'a été conçue une formule à 4 lentilles groupées par deux. Il s'agit d'un doublet divergent suivi d'un doublet convergent qui ressemble beaucoup à un agrandisseur télécentrique.
Ce dispositif peut se glisser dans un porte-oculaire de 2" (ou 50,4mm) et son dégagement est suffisant pour son emploi avec une roue à filtres ou un APN. Il multiplie la distance focale par 1,111 et il recule le plan focal de 41,72mm.
Au vu de ses performances, on serait tenté de le laisser en place lors de l'observation visuelle et cette pratique est même conseillée par les commerçants qui le vendent. Je le déconseille car on n'y gagne rien. En effet, avec la plupart des oculaires les images sont dégradées quand on le laisse à demeure. Ceux-ci ne sont pas conçus pour observer une image corrigée.
Ce correcteur de champ est bien adapté pour la photographie astronomique avec les télescopes d'amateur mais sa fabrication semble hors de portée des bricoleurs.
En fait, cette expression désigne habituellement un ensemble de deux lentilles accolées formant un doublet achromatique de puissance négative. Il est conçu pour allonger la distance focale. Souvent, il la double.
Avant de calculer une formule de doublet de BARLOW, il faut définir sa distance focale, les propriétés optiques des verres utilisés et le domaine spectral d'utilisation. Ces données imposent une valeur précise pour la puissance optique de chaque lentille mais l'opticien peut encore définir les cambrures. Dans l'article évoqué plus haut, Maurice PAUL nous montre qu'il est possible de choisir une solution qui élimine la coma d'un miroir parabolique.
Quand ils sont bien conçus, les doublets de BARLOW corrigent donc les aberrations de l'objectif du télescope. Ceci permet au possesseur d'un télescope de NEWTON ouvert à F/6 de faire de bons clichés au foyer de la Lune ou du Soleil. En effet, l'image fournie par un miroir parabolique d'une ouverture supérieure à F/10 est tellement limitée par la coma qu'elle n'est pas nette sur toute l'étendue de ces astres.
De plus, ce dispositif agrandisseur permet une utilisation beaucoup plus efficace des oculaires sur les télescopes très ouverts. Ceci est vrai pour l'observation visuelle et aussi pour la photographie planétaire à haute résolution par projection avec l'oculaire. C'est pour cela que la plupart des amateurs qui abordent cette technique sans BARLOW ont des difficultés pour faire une mise au point correcte car l'image est floue.
Notez bien que le doublet de BARLOW ne doit pas être employé pour un agrandissement différent de celui pour lequel il a été calculé, cela dégrade la qualité des images. Ce fait est souvent ignoré, il est pourtant flagrant.
Enfin, nous devons remarquer que les lentilles de Barlow (doublet ou triplet) donnent de mauvais résultats lorsqu'on les emploie sur des télescopes très ouvert (F/D<5).
Vous trouverez d'autres détails sur les lentilles de Barlow dans l'exposé sur les dispositifs agrandisseurs.
L'observateur autant que le constructeur a besoin de connaître les performances de ces dispositifs. Pour cela le calcul est très instructif mais il nécessite des efforts et une bonne culture mathématique. Une autre possibilité serait d'essayer un grand nombre de correcteurs se champ afin de bien se familiariser avec leurs performances. Cette dernière proposition serait utopique si les micro-ordinateurs n'existaient pas.
En effet, un logiciel de simulation optique permet d'étudier aisément les résultats que l'on peut obtenir avec n'importe quel correcteur sur n'importe quel instrument. Sur une autre page de ce site, nous vous proposons de télécharger librement le logiciel CORRECT 3.
CORRECT 3 est un logiciel de simulation optique qui permet d'étudier l'image fournie par un instrument optique d'observation, ce dernier pouvant être équipé d'un dispositif dioptrique (oculaire, Barlow, correcteur de champ...). Il analyse un ensemble de rayons lumineux répartis uniformément sur le miroir principal. Puis il montre l'image formée au foyer final ou l'image virtuelle que l'on peut observer en plaçant l'il à la sortie du dispositif (ex : image vue à travers l'oculaire).
CORRECT 3 ne tient pas compte de la nature ondulatoire de la lumière, il considère uniquement l'aspect géométrique de sa propagation. Autrement dit, pour définir le trajet d'un rayon lumineux, CORRECT néglige la diffraction. Il emploie seulement les formules de Descartes :
Réflexion ==> R = - I
Réfraction ==> N1.Sin( I ) = N2.Sin( R )
Avec : R = angle de réflexion, I = angle d'incidence, N1 et N2 = indices de réfraction
Pourquoi utiliser un logiciel de simulation optique ?
Pour le concepteur : Lors du calcul d'un dispositif optique, la théorie utilisée indique rarement toutes les propriétés ou les défauts que l'on obtiendra à la réalisation. Pour certaines combinaisons, la théorie fournit une famille de solutions apparemment équivalentes. Le logiciel permet au concepteur de vérifier la qualité de l'image, de choisir la meilleure solution ou d'optimiser les dimensions de la combinaison étudiée.
Pour le constructeur : Les rayons de courbure et les épaisseurs obtenues lors de l'usinage d'une lentille ne sont jamais parfaitement identiques aux caractéristiques désirées. Après avoir mesuré les dimensions réelles des différentes lentilles, l'opticien les indiquera au logiciel. Grâce à lui, il pourra vérifier si la précision de la réalisation est suffisante et éventuellement il pourra optimiser la position des lentilles en fonction de leurs caractéristiques réelles.
Pour l'observateur : L'utilisateur d'un télescope tirera, lui aussi, un grand profit de l'utilisation d'un programme de simulation optique. En effet, il lui permettra de choisir la meilleure formule d'oculaire pour son instrument. Très peu d'ouvrages sur l'optique astronomique prennent en compte les performances réelles des oculaires pour définir la qualité des images obtenues avec un télescope. Pourtant, quelques simulations d'oculaires démontrent facilement que ces accessoires forment l'élément le plus imparfait du télescope.
Pour le photographe du ciel : Le logiciel montrera à l'utilisateur d'un correcteur de champ les performances de cet élément. En faisant varier quelques paramètres, il pourra apprécier la précision nécessaire à son positionnement dans le télescope. De plus, il pourra vérifier la validité du dispositif agrandisseur qu'il utilisera pour agrandir les images planétaires. Il verra que les conseils donnés par de nombreux auteurs ne sont pas valables. Exemple : contrairement à ce qui est souvent affirmé un doublet de BARLOW ne doit pas être utilisé pour un agrandissement très différent de celui pour lequel il a été conçu. Autre exemple : un agrandissement important des images planétaires ne doit pas être réalisé avec un oculaire de grande distance focale.
La réalisation d'un correcteur de ROSS par un amateur ne pose pas de problème particulier. Ce dispositif peut même être fabriqué avec du verre à vitre. Par contre, il faut bien contrôler la qualité des matériaux employés pour la fabrication d'un correcteur de WYNNE ou d'un doublet de BARLOW.
Nous considérons que c'est surtout le correcteur de ROSS qui doit retenir l'attention du constructeur amateur. Pour l'usinage des deux lentilles qui le composent, nous employons une perceuse en guise de tour optique. Elle est maintenue verticalement avec le mandrin en haut. Nous avons percé le fond d'une cuvette en plastique avant de l'emmancher sur la partie cylindrique de la perceuse située sous le mandrin. De la sorte, cet accessoire ménager récupère les projections d'abrasifs ou de produit à polir. Les lentilles sont collées provisoirement avec de l'arcanson (mélange à chaud de 2/3 résine et 1/3 cire d'abeille) ou avec de la cire à cacheter sur des pièces métalliques. Ainsi disposées, les lentilles peuvent être maintenues par le mandrin de la perceuse ou par la main de l'opérateur. La figure 11 illustre en coupe ce dispositif.
Pour fabriquer des lentilles de 5cm de diamètre, la vitesse de rotation doit être approximativement de 100 tours par minute. Généralement, les variateurs incorporés aux perceuses ne permettent pas d'obtenir une bonne régularité de la rotation pour une vitesse aussi faible. Il peut alors être intéressant d'utiliser un bon variateur externe.
Le surfaçage des lentilles se fait d'une façon similaire à celui d'un miroir de télescope. L'usinage de chaque face nécessite un outil qui est constitué par un disque de verre de même diamètre. L'interposition d'un abrasif entre ces deux pièces provoque une usure qui sera plus importante au bord de la pièce de dessous et au centre de celle de dessus. Ce premier travail s'effectue avec du carborundum qui est un abrasif très dur. Puis, quand la courbure souhaitée est atteinte, une succession d'émeris de plus en plus fins est employée pour réduire le plus possible la rugosité de la surface. Ce doucissage est réalisé en alternant les positions des lentilles de façon à travailler autant l'extérieur que l'intérieur des surfaces sphériques. Ensuite, il ne reste plus qu'à polir après avoir recouvert l'outil avec de la poix optique. Le frottement de cette poix lubrifiée avec un mélange d'eau et de poussière d'oxyde de zirconium provoque un polissage rapide de la surface des lentilles.
L'amateur qui a déjà fabriqué un miroir de télescope déduira facilement tous les autres détails nécessaires pour la fabrication d'un correcteur de ROSS.
Je vous propose un exposé sur la réalisation d'un correcteur de champ.
Divers ouvrages peuvent être consultés avec profit pour apprendre les notions de base sur les correcteurs de champ.
Calcul des combinaisons optiques / Henri CHRETIEN - Editions MASSON
Les combinaisons optiques : pratique des calculs / Jean BURCHER - Editions de la REVUE D'OPTIQUE
Astrometry with mirrors and lenses / Franck E. ROSS / Astrophysical journal, mai 1933
Systèmes correcteurs pour réflecteurs astronomiques / Maurice PAUL / Revue d'optique, mai 1935
A new wide-field triple lens paraboloid field corrector / C. G. WYNNE / Montly notices n° 167 (1974)
Grâce à un correcteur de ROSS nous pouvons exploiter photographiquement un champ de 2x3° au foyer de TITAN, notre télescope de 150mm ouvert à F/4,6. Un autre correcteur de ROSS sur notre télescope de 400mm F/D=4,6 permet d'obtenir de bons clichés sur un champ de 44x66'. Sans correcteur, ce dernier instrument aurait un champ si réduit qu'il ne permettrait même pas de photographier correctement un objet comme l'amas globulaire M13.


Ce livre devrait figurer sur le bureau de tout opticien. Son génial auteur a disséminé ses inventions dans un grand nombre de domaines allant du cinéma (CinémaScope) aux chars de guerre (périscope) en passant par le Cataphote (utilisé en signalisation routière) ou par le télescope de RITCHEY-CHRETIEN. Il s'agit d'un cours d'optique théorique approfondi.
Cet ouvrage présente les techniques de calcul des combinaisons optiques. Il est plus orienté vers la pratique que le précédent. C'est un des rares livres d'optique à traiter de la conception des oculaires. Il comporte de nombreuses tables et applications numériques.
Cet article évoque une étude concernant l'avant-projet du télescope de 5 mètres du Mont Palomar. Pour l'élimination de la coma E. Ross préconise l'utilisation d'un couple de lentilles placées devant la plaque photographique, il ne donne pas les détails de construction.
Il s'agit d'une étude intéressante sur les correcteurs de champ. Entre autres choses, l'auteur démontre les caractéristiques du correcteur de champ à deux lentilles de ROSS et une formule de doublet de Barlow qui élimine la coma.
Description de deux correcteurs à trois lentilles.
 M31. Pose de 51mn sur TP2415 hypersensibilisé au foyer de TITAN, le télescope de 145mm de diamètre, F/D=4,8 avec Correcteur de champ (formule de ROSS à 2 lentilles). |
La fabrication d'un correcteur de ROSS ne demande pas un gros investissement ni en temps ni en argent. Nous encourageons tous les bricoleurs d'instruments d'observations qui possèdent un télescope de NEWTON très ouvert à tenter l'expérience. Ils redécouvriront leur instrument.
 M63 dans les CHIENS DE CHASSE. Cliché pris sur TP2415 hypersensibilisé au foyer de ALCOR, notre télescope de 260mm de diamètre F/D=4,6 avec correcteur de champ (formule de ROSS à 2 lentilles taillées dans du verre à vitre ordinaire). |





