NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
La diffraction de la lumière
La diffraction caractérise les déviations subies par la direction de propagation des ondes (lumineuse, acoustique, radio, rayon X...) lorsqu'elles rencontrent un obstacle.
Ce phénomène semble avoir été observé pour la première fois avant 1500 par Léonard de VINCI (artiste et savant italien, né à Florence en 1452 et mort en France près d'Amboise en 1519).
Les premières descriptions précises ont été écrites par le père jésuite italien Francesco Maria GRIMALDI (1618 - 1663) dans un traité publié après sa mort.
Le physicien néerlandais Christiaan HUYGENS (1629 - 1695) fut le premier à proposer une théorie ondulatoire de la lumière qui traitait notamment de la diffraction. Il semble qu'il ignorait les travaux de GRIMALDI.
C'est en 1815 et 1818 qu'Augustin FRESNEL (physicien français 1788 - 1827) présenta ses deux mémoires sur sa théorie des propriétés de la lumière dans lesquels il donna une interprétation des phénomènes de diffraction.
Sur le site de bibnum, on trouve un intéressant exposé de Jean-Louis Basdevant sur Fresnel et son mémoire sur la diffraction de la lumière.
Limite de l'ombre d'un bord droit
On savait donc, depuis le 15ième siècle, qu'on peut trouver des zones lumineuses en des endroits où la propagation rectiligne de la lumière donnerait de l'ombre et des zones d'ombre en des régions de plein éclairement.
La figure 1 nous montre un exemple de ce comportement de la lumière.
Il s'agit d'une ombre portée par un objet au bord rectiligne sur un écran éclairé par une source ponctuelle.
Si l'éclairement était obtenu avec une source étendue comme le Soleil (par exemple), la limite de l'ombre serait relativement floue et il y aurait une transition progressive entre l'éclairement et l'ombre.
Si la lumière se propageait toujours en ligne droite, avec une source ponctuelle il y aurait une transition brutale entre la partie éclairée et l'ombre.
En fait, on constate un phénomène plus complexe.

Un peu de lumière se glisse dans l'ombre et un système de franges apparaît sur la partie éclairée de l'écran. La figure 2 détaille cet aspect.

Quand l'objet est situé à 1 mètre de l'écran, on peut percevoir le système de franges sur une largeur de quelques millimètres, voire 1 centimètre dans les meilleures conditions en lumière monochromatique. Toutefois, avec une lumière blanche on remarque seulement les premières franges.
A l'endroit où devrait se faire précisément la transition lumière-ombre on mesure une intensité lumineuse de 25% et elle diminue rapidement quand on se dirige vers l'intérieur de l'ombre.
En se dirigeant vers la partie éclairée, l'intensité lumineuse croit rapidement pour atteindre une valeur nettement supérieure à celle qu'elle aurait sans l'obstacle puis elle suit une oscillation amortie dont la période diminue en s'éloignant de la limite de l'ombre.
Pour expliquer ce comportement de la lumière, Huygens et Fresnel ont énoncé les règles suivantes :
La position du front d'onde (surface d'onde) à tout instant ultérieur est l'enveloppe de toutes ces ondelettes (Huygens).
Ces sources secondaires sont cohérentes, cela signifie qu'elles peuvent interférer (Fresnel).
Je considère qu'il faut ajouter que ces sources secondaires rayonnent uniquement dans le demi-espace vers lequel se propage le front d'onde. En effet, si on considère uniquement l'énoncé de Huygens, ces ondelettes sphériques devraient aussi se propager "vers l'arrière"...
On parle de diffraction de Fresnel lorsqu'on examine la diffraction en champ proche. Dans ce cas, le front d'onde est courbe.
Ce cas est à distinguer de la diffraction de Fraunhofer qui considère des ondes planes (fournies par une source ponctuelle et éloignée) et une figure de diffraction étudiée à grande distance.
Considérons maintenant un montage comprenant une source lumineuse monochromatique, ponctuelle et éloignée qui éclaire une fente étroite. Celle-ci laisse passer un faisceau de lumière qui se dirige vers un écran sur lequel nous analysons la répartition de l'éclairement.
Nous nous limiterons ici au cas d'une onde plane incidente qui est parallèle au plan qui contient la fente (incidence normale).
Nous sommes dans le cas de Fraunhofer, c'est à dire que les distances sont grandes par rapport à la largeur de la fente.

Nous obtenons une figure de diffraction symétrique par rapport au plan qui contient la source et la fente. Elle se compose d'une bande lumineuse centrale encadrée par un réseau de franges parallèles d'intensités décroissantes.
Toutes les franges ont une même largeur angulaire à l'exception de la frange centrale qui est deux fois plus large.
D'après le principe d'HUYGENS-FRESNEL, chaque point de la surface de la fente rayonne dans toutes les directions du demi-espace sortant (figure 4).
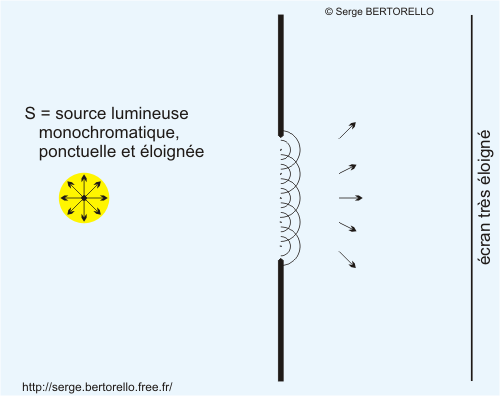
Pour déterminer l'amplitude de l'onde lumineuse reçue par un point de l'écran, il faut additionner au niveau de ce point les amplitudes qu'il reçoit de toutes ces ondes parties de la fente. Suivant la phase des rayonnements à leur arrivée sur ce lieu, certaines de ces interférences lumineuses seront constructives et d'autres destructives provoquant par endroit un éclairement ou bien une zone sombre.
Faisons tout d'abord une première analyse des interférences entre ces ondelettes pour les directions les plus remarquables en Observant la figure 5.

La première image (figure 5A) illustre les rayons dans la direction perpendiculaire au plan de la fente. Dans ce cas, puisque nous sommes en incidence normale, ils ne sont pas déviés, ils sont donc tous en phase et leurs effets s'ajouteront à leur arrivée sur l'écran provoquant ainsi une zone lumineuse sur l'écran : c'est la frange centrale.
Sur l'illustration suivante (figure 5B), nous avons illustré les rayons dont l'orientation fait un angle en sortie tel que le rayon le plus bas du faisceau a pris un retard d'une longueur d'onde sur le rayon le plus haut (le sinus de l'angle vaut donc λ/a). Ce décalage varie progressivement entre ces deux rayons. Ainsi, nous remarquons que le rayon central est décalé d'une demi-longueur d'onde par rapport au rayon le plus haut. Ces deux rayons sont donc en opposition de phase et leurs effets s'annulent en arrivant sur l'écran.
En poursuivant notre analyse, nous voyons que le rayon situé immédiatement sous le rayon supérieur est lui aussi en opposition de phase avec le rayon qui est immédiatement sous le rayon central. Leurs effets se contrarient donc.
En fait, chaque rayon de la moitié supérieure de la fente annule le rayon qui lui correspond dans la moitié inférieure. Cette direction de propagation correspond à une zone sombre, c'est la première frange sombre.
Il y a bien entendu le même phénomène pour l'orientation symétrique par rapport à l'axe central (vers le bas). Nous venons donc d'expliquer les deux franges sombres qui encadrent la frange centrale.
En considérant des rayons encore plus inclinés, on arrive à un nouveau minimum pour une orientation telle que le rayon le plus bas du faisceau a pris un retard de deux longueurs d'onde sur le rayon le plus haut (le sinus de l'angle vaut donc 2.λ/a), c'est la figure 5C. Le même raisonnement peut être tenu ici mais il faut diviser la largeur de la fente en quatre parties au lieu de deux. Le rayon supérieur est en opposition de phase avec le rayon qui est un quart de largeur de fente plus bas, ils s'annulent tous deux. De même le rayon central annule celui qui est un quart de largeur plus bas, etc. Les rayons s'annulent à nouveau 2 à 2. Idem pour l'orientation symétrique vers le bas.
Toutes les franges sombres s'expliquent ainsi...
La figure suivante nous informe quantitativement sur un exemple de résultat.

Si nous analysons l'amplitude de l'éclairement en un point de l'écran avec l'outil mathématique, nous obtenons la relation suivante:
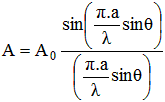
avec : A0 = amplitude lumineuse sur l'axe
A = Amplitude lumineuse à la distance angulaire θ de l'axe
a = Largeur de la fente
λ = longueur d'onde de la lumière
Le résultat obtenu peut être positif ou négatif selon la combinaison des rayons et de leur phase au point considéré.
Pour obtenir l'intensité de l'éclairement reçu par un point de l'écran, il suffit d'élever au carré cette expression :
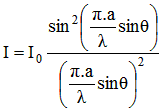
avec : I0 = intensité lumineuse sur l'axe
I = Intensité lumineuse à la distance angulaire θ de l'axe
Bien entendu, comme on pouvait s'y attendre, la valeur de l'intensité ne peut pas être négative. Elle est positive ou nulle.
Si on veut repérer les points étudiés avec une distance plutôt qu'un angle, il suffit de remplacer sinθ par l'expression suivante :

avec : D = distance entre la fente et l'écran
x = distance à l'axe mesurée sur l'écran
La distance angulaire qui sépare l'axe du premier minimum est α :
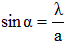
Cette distance mesurée en longueur sur l'écran est r :
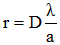
Considérons le cas pratique qui nous a permis d'obtenir le graphique de la figure 6, il comporte une largeur de fente a = 0,03mm et un écran placé à une distance D = 0,25m de cette fente. Nous obtenons pour une longueur d'onde λ = 0,56µm :
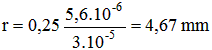
Diffraction par une fente double
Nous avons évoqué précédemment l'expérience de Young en négligeant les effets de la diffraction des fentes sur la luminosité des franges produites.
En fait, comme nous pouvons l'imaginer maintenant, la luminosité des franges produites dans cette expérience est modulée par le phénomène de diffraction de la lumière par les fentes.
La figure 7 nous montre une demi-figure de diffraction obtenue avec l'expérience de Young, elle est symétrique par rapport à l'axe du montage. Il s'agit du montage précédent auquel nous avons ajouté une deuxième fente parallèle à la première. Nous considérons toujours un rayonnement monochromatique et des conditions de Fraunhofer.

Ce graphique nous montre les franges d'interférence de Young dont l'amplitude est modulée par la diffraction des fentes.
Pour comprendre la formation de ces franges d'interférence, nous pouvons utiliser un raisonnement semblable à celui qui nous a permis de comprendre la formation des franges sombres dans la figure de diffraction d'une fente. Mais ici, nous nous intéresserons aux franges brillantes.
D'après le principe d'HUYGENS-FRESNEL, chaque point de la surface de chaque fente rayonne dans toutes les directions du demi-espace sortant. Observons la figure 8.

Pour la direction perpendiculaire au plan qui contient les fentes (figure 8A), les rayons émergeants ne sont pas déviés, ils restent donc en phase et ils forment donc une frange brillante.
Quand on s'écarte progressivement de cette direction, on constate que les déphasages des deux rayons se contrarient provoquant une baisse de luminosité jusqu'à ce que les rayons soient en opposition de phase pour provoquer la première frange sombre.
Ensuite les interférences redeviennent de plus en plus constructives pour former une frange brillante dont le maximum est atteint quand le déphasage entre les deux faisceaux atteint une longueur d'onde (figure 8B). Ici, le rayon fait avec l'axe un angle dont le sinus vaut λ/b.
Et ainsi de suite, il y a une frange brillante chaque fois que le déphasage atteint un nombre entier de longueurs d'onde.
L'intensité est décrite par l'expression suivante :
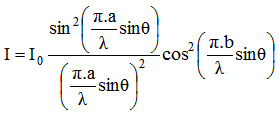
avec : b = distance entre les fentes.
La distance angulaire entre deux franges consécutives est égale à λ/b (en radians). Pour obtenir la valeur de cette distance sur l'écran, il suffit de multiplier ce résultat par la distance entre les fentes et l'écran.
Reprenons notre exemple pratique précédent auquel nous ajoutons une deuxième fente à b = 0,3mm de la première, nous obtenons la valeur "i" de cet interfrange sur l'écran en effectuant le calcul suivant :
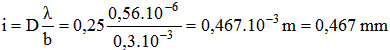
Remarque : Pour notre montage, nous avons choisi de prendre une distance entre fentes égale à dix fois la largeur des fentes. Par conséquent, une fois toutes les dix franges, une frange brillante correspond à un minimum dû à la diffraction. C'est pour cela que le dixième maximum n'apparaît pas ainsi que le vingtième, le trentième, etc. Pourtant, la frange centrale n'est pas concernée par cette extinction.
Le nombre de franges dans le pic central de diffraction est proportionnel au rapport b/a et il est indépendant de la longueur d'onde.
Si nous rajoutons des fentes à notre montage, nous obtenons un réseau. Un réseau est constitué par un grand nombre de fentes parallèles et équidistantes. La figure 9 nous montre comment se comporte l'intensité selon le nombre de fentes.

Quand nous augmentons le nombre de fentes N, les franges deviennent de plus en plus étroites et il apparaît de nouvelles petites franges dont l'amplitude est d'autant plus faible que N est grand.
Ainsi quand le nombre de fentes est très grand, on ne remarque plus que les franges principales qui sont très fines.
La formule générale suivante indique l'intensité lumineuse diffractée dans la direction θ par un réseau de N fentes :
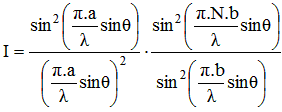
La position des franges, ou plutôt des raies, est directement liée à la longueur d'onde de la lumière. La figure 10 nous montre comment notre réseau disperse les rayonnements de 3 longueurs d'onde différentes correspondant à des couleurs bleue, verte et rouge.

Dans l'axe du réseau, appelé "ordre 0", les couleurs ne sont pas dispersées. Autour du premier groupe de franges, appelé "ordre 1", la dispersion spectrale est évidente mais les "ordres" suivants se chevauchent et cela complique l'interprétation de la dispersion. On constate par exemple que l'extrême violet du troisième ordre vient se mélanger avec le rouge du deuxième ordre.
Les réseaux de diffraction sont communément employés pour analyser la composition spectrale de la lumière dans des spectroscopes (pour l'étude visuelle) ou dans des spectrographes (pour l'étude sur un enregistrement photographique ou graphique).
Les réseaux employés dans ces appareils de mesure sont beaucoup plus dispersifs que celui que nous avons évoqué dans la figure 9. Ces réseaux de diffraction possèdent une surface gravée de plusieurs centaines de traits au millimètre en guise de fentes multiples.
Les spectroscopes et les spectrographes peuvent aussi être conçus autour d'un prisme comme nous l'avons vu précédemment.
La figure suivante nous présente le principe d'un spectroscope. Celui-ci est équipé d'un réseau de diffraction mais on pourrait aussi utiliser un prisme de verre, il suffirait de le disposer à la place du réseau. Le reste du montage serait semblable.
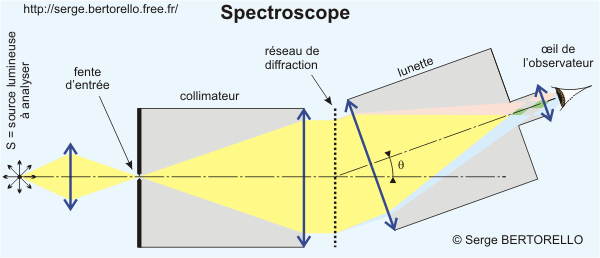
La lumière à analyser est concentrée par une première lentille sur la fente d'entrée. Cet élément est nécessaire pour bien contrôler la direction d'entrée du faisceau lumineux, il faut que celui-ci "éclaire" uniformément la lentille suivante.
La fente d'entrée est positionnée au foyer objet d'une lentille collimatrice qui forme son image à l'infini. Elle aplanit le front d'onde lumineux afin qu'il aborde le réseau dans les conditions de Fraunhofer.
Une lunette concentre ensuite le faisceau émergeant du réseau dans l'il de l'observateur pour lui permettre d'observer le spectre. Il est donc examiné dans les conditions de Fraunhofer. Cette lunette peut pivoter autour du centre du réseau afin d'explorer l'ensemble du spectre. Une mesure de son orientation (angle θ) permet de déduire la longueur d'onde visée.
L'utilisateur voit dans l'oculaire de la lunette la juxtaposition d'une multitude d'images de la fente d'entrée, dont la couleur de chacune (sa longueur d'onde) correspond à une orientation différente.
Si une seule longueur d'onde est absente dans la lumière étudiée, on voit une raie sombre (ou raie d'absorption) dans le spectre à l'emplacement qui lui correspond. C'est en quelque sorte une image "noire" de la fente.
Inversement, si la lumière comprend une seule longueur d'onde λ (un laser par exemple), c'est alors une seule raie (raie d'émission) que l'on voit dans l'oculaire. Bien entendu, la position de cette raie correspond à l'orientation selon l'angle θ = λ/b.

La composition spectrale d'une lumière caractérise le corps qui l'a émise ainsi que les corps transparents qu'elle a traversés ou bien les corps opaques sur lesquels elle s'est réfléchie. La spectroscopie a apporté d'immenses services à l'étude de la physique et de l'astronomie. Grâce à elle, des chercheurs peuvent étudier à distance la composition chimique des étoiles ou les conditions physiques qui règnent à la surface du Soleil...
Faisceau limité par une ouverture circulaire
Ce cas particulier est très important pour l'étude des instruments d'observation télescopique.
Nous sommes ici dans le cas d'un objectif à contour circulaire et sans obstruction centrale qui forme l'image à son foyer d'une source ponctuelle éloignée. C'est précisément la situation d'une lunette astronomique dirigée sur une étoile.

Je rappelle qu'une étoile est tellement éloignée qu'elle n'a aucune dimension appréciable, elle constitue vraiment un point lumineux éloigné à l'infini.
Quand il est dirigé vers une étoile, l'instrument d'observation que nous avons choisi fournit une image très différente de l'apparence de cet astre. Voici ci-contre l'image stellaire obtenue par un instrument d'observation parfait dans les conditions idéales (bonne transparence, pas de turbulence atmosphérique...). Il faut employer un fort grossissement pour l'examiner, d'une valeur au moins égale au double du diamètre de l'objectif exprimé en millimètres.
Cette figure de diffraction a été décrite par Sir George Biddell AIRY (astronome britannique 1801 - 1892). La partie centrale circulaire est appelée "tache de diffraction" ou "disque de Airy". Elle limite la finesse des images télescopiques.
Cette image circulaire est entourée d'un système d'anneaux concentriques dont l'éclat va en diminuant rapidement. C'est surtout le premier anneau que l'on perçoit, rarement le second (du moins quand rien ne vient perturber l'observation comme la turbulence atmosphérique, des aberrations...).
L'étude des intensités lumineuses au sein de cette figure de diffraction est plus compliquée que celle de la fente. C'est parce que la fente possède une largeur constante contrairement à notre ouverture circulaire.

Cette courbe est obtenue avec la relation suivante :
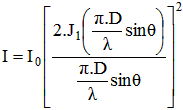
avec : I0 = intensité lumineuse au centre de la tache.
I = intensité lumineuse à la distance angulaire θ de l'axe
D = diamètre de l'objectif.
λ = longueur d'onde de la lumière
J1 = fonction de Bessel du premier ordre
J1 est la fonction de Bessel du premier ordre, elle s'applique sur la partie entre-parenthèses.
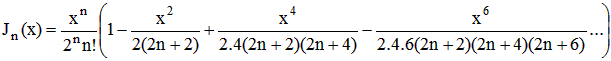
Dans le cas présent, nous utilisons cette fonction avec l'ordre n = 1 et la formule précédente se réduit à l'expression suivante:
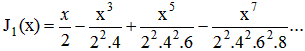
Cette fonction est disponible directement dans certaines calculatrices ou dans certains logiciels comme, par exemple, le tableur Excel de Microsoft.
Le premier anneau sombre est à la distance angulaire θ1 du centre de la tache et à la distance linéaire r1 :
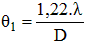
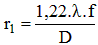
Avec : f = distance focale de l'instrument d'observation
θ1 est exprimé en radians.
Exemple : avec un objectif de 200mm de diamètre et 1m de distance focale, nous obtenons :
-
θ1 = 0,705 "
r1 = 3,42 µm
Cela signifie que la dimension angulaire de la tache de diffraction diminue quand on augmente le diamètre de l'instrument d'observation. Un gros télescope montre des images plus fines qu'un petit.
Malgré cela, il faut remarquer que la dimension linéaire de cette tache dépend seulement du rapport F/D (si on oublie λ). Les taches de diffraction de deux instruments de même rapport F/D auront donc des dimensions linéaires identiques même si l'un deux a un diamètre de 10cm et l'autre 1m.
Ces dernières formules nous indiquent aussi que les dimensions de la figure de diffraction dépendent de la longueur d'onde de la lumière. Cela signifie que l'image de diffraction devrait être irisée. En fait, le dégradé de couleur auquel nous nous attendons n'est pas perceptible dans les conditions habituelles d'observation des étoiles.
Contrairement à la distribution régulière des franges dans le cas de la diffraction par une fente, ici l'intervalle entre les anneaux successifs n'est pas rigoureusement constant. Considérons que les rayons angulaires des anneaux sont donnés par l'équation suivante :
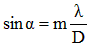
Le tableau suivant nous indique les différentes valeurs de m pour les extremums relatifs de la courbe précédente avec les valeurs des intensités correspondantes.
| m | 0 | 1,22 | 1,64 | 2,23 | 2,69 | 3,24 | 3,72 | 4,24 | ||||
| IMaxima | 1 | - | 0,017 | - | 0,004 | - | 0,0016 | - | ||||
| IMinima | - | 0 | - | 0 | - | 0 | - | 0 | ||||
| Intensité relative | 83,8 % | 7,2 % | 2,8 % | 1,5 % | ||||||||
Ce tableau nous indique aussi que la tache centrale ne reçoit que 83,8% de l'intensité lumineuse totale. Les 16,2% restants sont distribués dans les anneaux, surtout dans le premier qui retient 7,2% du total.
Influence des aberrations - règle de Lord Rayleigh
Jusque-là nous avons raisonné sur un objectif parfait dont la finesse des images est limitée uniquement par la diffraction mais que se passe-t-il avec un objectif imparfait?
Lorsque les rayons lumineux qui forment l'image d'une étoile n'arrivent pas suffisamment concentrés dans le centre de la tache de diffraction, l'intensité lumineuse du pic central s'affaiblit en faveur des anneaux qui deviennent plus lumineux.
Un exemple de détérioration grave de l'image de diffraction est apporté par certains instruments qui montrent beaucoup trop d'anneaux de diffraction autour des images stellaires. Vous comprendrez que ces anneaux surnuméraires ne sont pas un indice de bonne qualité de l'objectif.
Ainsi les défauts de l'objectif, qu'ils soient dus à la conception ou à la précision de l'usinage, ne provoquent pas un agrandissement de la tache centrale de la figure de diffraction stellaire mais ils entraînent une répartition anormale de l'énergie. L'éclat excessif des anneaux cause une perte de contraste nuisible à l'étude des alentours immédiats des étoiles ou des fins détails planétaires.
Si les défauts n'ont pas une symétrie de révolution (astigmatisme, coma), l'intensité lumineuse des anneaux est renforcée seulement dans certaines directions.
L'image d'une étoile est formée par un front d'onde sphérique qui rétrécit en se propageant jusqu'à se concentrer au foyer. Lord Rayleigh (Lord John William Strutt Rayleigh 1842-1919) a défini une tolérance sur la forme de ce front d'onde : les défauts du front d'onde qui forme la tache de diffraction sont négligeables si celui-ci est entièrement compris entre deux sphères écartées de λ/4. On dit alors que le système optique est parfait car son pouvoir de résolution est limité seulement par la diffraction.
Un tel défaut de λ/4 peut être provoqué par une anomalie de surface de λ/2 sur l'objectif d'un réfracteur (lentille) ou par un défaut de λ/8 sur la surface d'un objectif réflecteur (miroir). C'est pour cela, afin d'éviter les ambigüités, que la précision de fabrication des objectifs est indiquée sur la forme du front d'onde et non pas sur la forme de leur surface. Toutefois, cette convention n'est pas respectée par certains vendeurs de télescopes qui préfèrent indiquer la précision sur le miroir en laissant supposer qu'il s'agit de l'onde car c'est plus flatteur pour l'instrument (c'est donc une pratique mensongère...).
Pouvoir séparateur des instruments d'observation
Considérons deux étoiles de directions voisines et un instrument d'observation dont l'axe est précisément dirigé vers l'une d'elles. Nommons α l'angle formé par les directions de ces deux étoiles.

Si l'angle α est assez grand pour que les disques de diffraction ne se chevauchent pas, ces astres seront vu séparés (avec un grossissement adapté).
Si cet angle est trop petit, on ne séparera pas les disques des deux étoiles et la tache centrale pourra sembler allongée comme l'illustre la figure ci-contre.
Les deux images stellaires se superposent simplement. Leur chevauchement ne provoque pas de nouvelle figure d'interférences car les sources lumineuses concernées (les étoiles) ne sont pas cohérentes entre-elles, leurs lumières respectives n'interfèrent pas entre-elles.

La limite à partir de laquelle on affirme que les étoiles sont séparées est bien entendu discutable. Lord Rayleigh estimait que les étoiles sont séparées quand elles sont éloignées d'une distance au moins égale au rayon du premier anneau sombre. En pratique cette idée est valable seulement si les étoiles ont un éclat apparent semblable.
La figure 16 illustre le cas limite avec deux étoiles de même éclat apparent séparées par un angle égal au rayon du premier anneau sombre.
Dans ce cas limite, nous avons :
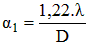
Si nous exprimons α1 en secondes d'arc et D en centimètres et que nous choisissons λ = 0,55µm (correspondant au maximum de sensibilité de l'il), cette relation devient :
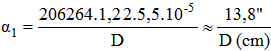
Léon Foucault (physicien français 1819-1868) a réalisé une étude expérimentale sur le pouvoir séparateur des objectifs et il a trouvé une relation voisine :
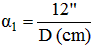
C'est souvent cette formule qui est employée pour définir le pouvoir séparateur d'un instrument d'observation, notamment par les vendeurs car elle est plus flatteuse que la précédente. Elle indique qu'un télescope de 12cm de diamètre sépare deux étoiles écartées de 1" (1 seconde d'arc) alors qu'avec le critère de Rayleigh il faut un objectif plus gros, de 13,8cm de diamètre, pour obtenir cette performance.
C'est pour cela que certains auteurs expriment que le pouvoir de résolution des objectifs est égal au critère de Rayleigh multiplié par 0,85. D'autres proposent que la résolution de 1" est atteinte par un diamètre de 11cm seulement...
Je vous laisse le soin, ami lecteur, de juger ce qui est important (ou pas) dans ces considérations sur le pouvoir de résolution des instruments d'observation.
Par ailleurs, la différence d'éclat entre les deux composantes d'un couple stellaire perturbe le pouvoir résolvant d'un instrument. Un cas célèbre est constitué par l'étoile la plus brillante du ciel (après le Soleil) SIRIUS qui est en fait une étoile double dont les éclats des deux astres diffèrent d'une dizaine de magnitudes.
On nomme SIRIUS A l'astre principal et SIRIUS B le compagnon (qui est une naine blanche). Ils sont actuellement séparés par une dizaine de secondes d'arc et leur résolution devrait donc être à la portée d'un petit instrument. Toutefois, la grande différence d'éclat rend difficile la détection du compagnon et c'est avec une lunette de 46 cm de diamètre que Alvan Graham Clark (Astronome et opticien américain 1832 1897) l'a découvert visuellement en 1862.
Conséquences de l'obstruction centrale
Considérons maintenant un faisceau limité par une ouverture circulaire avec obstruction centrale, c'est le cas d'un télescope dont une partie du faisceau incident est obstruée par la silhouette du miroir secondaire.
La première conséquence de cette obstruction est évidemment une perte de luminosité de l'image. Habituellement, la silhouette du miroir secondaire a un diamètre compris entre 2 et 3 dixièmes de celui du miroir principal. Elle provoque donc une perte de lumière de quelques pourcents de l'intensité lumineuse incidente, ce qui correspond à une perte de quelques centièmes de magnitude sur l'éclat apparent des astres observés.
Cet affaiblissement lumineux des images est généralement négligeable mais une autre conséquence est préoccupante, c'est l'augmentation de la luminosité des anneaux de diffraction comme nous le montrent les courbes la figure 17.
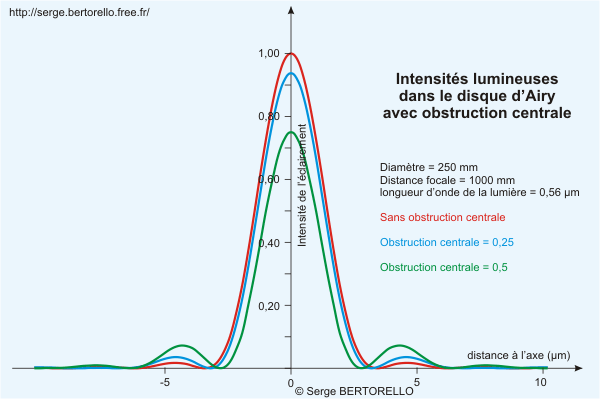
Nous constatons que la perte de luminosité entraîne une diminution de la hauteur du pic central et, malgré cela, nous assistons à une augmentation de l'intensité lumineuse du premier anneau qui dégrade le contraste des fins détails sur les images.
Depuis de nombreuses années, le livre de Jean TEXEREAU "La construction du télescope d'amateur" est la référence incontournable des opticiens amateurs, Jean TEXEREAU est né 3 février 1919 et il est mort le 6 février 2014. Cet ouvrage nous indique notamment la répartition de l'énergie lumineuse dans les anneaux de diffraction en fonction de l'obstruction centrale. Il s'agit du tableau suivant :
| OBSTRUCTION RELATIVE | 0,0 | 0,1 | 0,2 | 0,3 | 0,5 |
| Tache centrale | 83,8 % | 81,8 % | 76,4 % | 68,2 % | 47,8 % |
| 1eranneau | 7,2 % | 8,7 % | 13,7 % | 21,8 % | 35,2 % |
| 2ièmeanneau | 2,8 % | 1,9 % | 0,7 % | 0,5 % | 7,2 % |
| 3ièmeanneau | 1,5 % | 2,4 % | 4,0 % | 2,5 % | 0,2 % |
| Tous les anneaux | 16,2 % | 18,2 % | 23,6 % | 31,8 % | 52,2 % |
Dans ce tableau, l'obstruction relative est considérée comme étant le rapport du diamètre de la silhouette qui obstrue sur le diamètre de l'objectif. Ainsi, pour un télescope de Newton dont le miroir principal a 200mm de diamètre et dont le miroir plan a un petit axe de 50mm nous avons une obstruction de 50/200 = 0,25.
Une obstruction de 0,1 dégrade très peu la tache de diffraction. Avec une valeur de 0,2, on commence à percevoir le renforcement du premier anneau et avec une valeur de 0,3 la dégradation des fins détails devient difficilement tolérable sur les images planétaires.
L'attention de certains pourrait être attirée par la diminution du rayon de la tache centrale sous l'influence de l'obstruction centrale... mais elle ne compense pas la mauvaise influence de l'accroissement de la luminosité des anneaux sur la finesse et le contraste des images.
Dans son livre "Astronomical Optics", Daniel J. Schroeder nous donne les valeurs des coefficients des premiers anneaux sombres qui entourent le disque d'Airy.
| OBSTRUCTION RELATIVE | W1 | W2 | W3 |
| 0,00 | 1,220 | 2,233 | 3,238 |
| 0,10 | 1,205 | 2,269 | 3,182 |
| 0,20 | 1,167 | 2,357 | 3,087 |
| 0,33 | 1,098 | 2,424 | 3,137 |
| 0,40 | 1,058 | 2,388 | 3,300 |
| 0,50 | 1,000 | 2,286 | 3,491 |
| 0,60 | 0,947 | 2,170 | 3,389 |
Pour calculer le rayon αx d'un anneau sombre, il suffit de multiplier le coefficient correspondant par la longueur d'onde λ de la lumière considérée puis de diviser le résultat par le diamètre D de l'objectif.
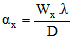
Ainsi on peut constater que le rayon du second anneau sombre atteint un maximum pour une obstruction centrale de 0,3 puis il diminue pour les obstructions supérieures.
Le concepteur d'un télescope doit donc choisir la dimension du miroir secondaire afin d'obtenir un champ de pleine lumière suffisant mais sans trop altérer la tache de diffraction. La valeur de cette obstruction de compromis ne doit pas dépasser une limite qui varie selon les auteurs. Moi-même, j'évite de lui donner une valeur supérieure à 0,25 et j'espère vous avoir fourni assez d'informations pour vous faire votre propre opinion.

