NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
La Lumière
"Heureux les fêlés car ils laissent passer la lumière" Michel Audiard (1920 - 1985).
L'optique est la science de la lumière et des images qu'elle peut former.
Nature de la lumière
Expérience de Young (Thomas YOUNG, 1773 - 1829)
Nous avons employé jusqu'ici la notion de rayon lumineux. Elle est simple et efficace pour l'étude de la formation des images mais elle ne permet pas d'expliquer le résultat de certaines expériences.
Considérons l'exemple des fentes de Young illustré sur la figure 1. Ce dispositif est constitué par une petite source lumineuse dont la lumière éclaire un écran après avoir traversé un masque comportant deux fentes fines et parallèles.
Si la lumière avait uniquement les propriétés géométriques que nous avons examinées, il apparaîtrait deux traits lumineux sur l'écran. C'est effectivement ce qu'il advient lorsque les fentes sont larges. Par contre, si les fentes sont étroites (1/10 mm par exemple) nous constatons les faits suivants :
Pour expliquer de telles expériences, il nous faut considérer que la lumière est un phénomène vibratoire. C'est une ondulation d'un champ électromagnétique comparable aux ondulations que l'on peut créer en agitant un doigt sur la surface d'un récipient d'eau.
C'est la théorie ondulatoire de la lumière. L'onde lumineuse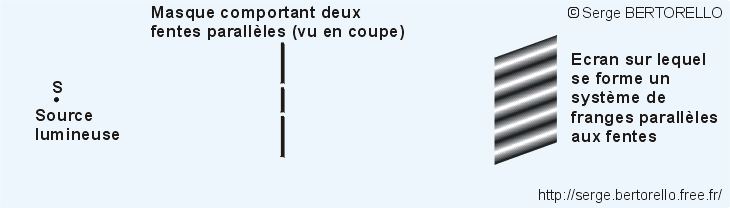
- Avec une seule fente, l'écran est entièrement éclairé.
- Avec deux fentes parallèles, un système de franges lumineuses alternativement claires et sombres se forme sur l'écran. Ces franges sont parallèles aux fentes du masque.
- A l'endroit des franges lumineuses l'écran est plus brillant que lorsqu'il n'y a qu'une seule fente. Cela signifie qu'avec la deuxième fente, certaines zones de l'écran sont plus brillantes alors que d'autres sont plus sombres.
- La frange centrale est toujours brillante.
D'après cette théorie la lumière est un phénomène périodique qui peut être représenté par une fonction sinusoïdale du temps (figure 2).
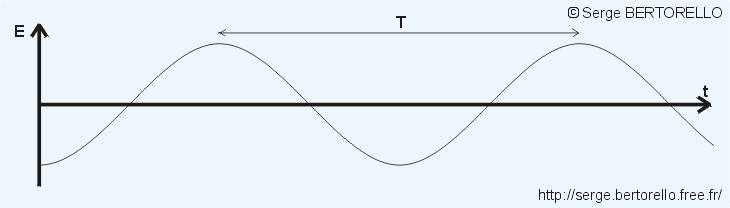
Cette figure représente le champ électrique que subit un point éclairé par une source lumineuse.
E représente l'amplitude du champ électrique et t désigne le temps. T est la période du signal, cela signifie que le champ électromagnétique reprend la même valeur au bout du temps T.
Puisque la lumière se propage avec une vitesse finie elle est aussi périodique dans l'espace (figure 3). Cette vitesse se nomme la célérité de la lumière, dans le vide elle vaut environ 300 000 Kilomètres par seconde. Le mot célérité désigne la vitesse de propagation d'une onde, alors que le mot vitesse est employé lorsqu'il y a un déplacement (de matière).
Cette fois l'axe horizontal (x) représente la distance à la source. Cette courbe sinusoïdale se déplace le long de l'axe x à la vitesse de la lumière. En conséquence, pour chaque point de cet axe le champ varie périodiquement de la façon décrite sur la figure 2. Autrement dit, la longueur d'onde de la lumière est la distance qu'elle parcourt pendant une période de son alternance.
Pour désigner la longueur d'onde, on utilise habituellement la lettre grecque λ (lambda).
Les interférences lumineuses
Les interférences lumineuses sont les combinaisons entre des ondes lumineuses. Dans ce cas les deux rayons incidents sont en phase car leurs maximums (par exemple) interviennent au même moment. Dans le cas général la situation est intermédiaire, les amplitudes sont différentes et la phase est quelconque comme l'illustre la figure 6.
L'expérience de Young que nous avons décrite plus haut est une manifestation des interférences lumineuses mais c'est un autre phénomène appelé "diffraction" qui explique la diffusion de la lumière. Les deux fentes peuvent être considérées comme deux sources lumineuses identiques et en phase qui rayonnent dans toutes les directions. Les rayons lumineux qu'elles émettent interférent au niveau de l'écran pour former un ensemble de franges.
La distance entre l'écran et chacune des deux fentes varie selon l'emplacement de l'écran considéré. Les rayons qui arrivent sur la frange centrale parcourent la même distance pour les deux fentes. Ils sont donc en phase et leurs effets s'ajoutent. Pour les autres endroits de l'écran, les rayons issus des deux fentes ont parcouru des distances différentes. Ils arrivent donc avec des phases différentes. Ils ajoutent ou retranchent leurs effets suivant la différence de phase. Pour illustrer les interférences lumineuses, on utilise parfois l'analogie qu'il y a entre l'onde lumineuse et les vagues à la surface de l'eau. Il peut aussi y avoir des interférences avec les vagues.
Considérons par exemple les vagues d'étrave engendrées par l'avancement d'un bateau. Il s'agit d'une oscillation sinusoïdale de la surface de l'eau qui se développe à partir de l'avant du navire et qui provoque une part non négligeable de la résistance à l'avancement.
Pour faciliter la progression du bateau on l'équipe parfois d'un bulbe d'étrave. C'est un renflement de la proue du navire destiné à former une vague à l'avant de celui-ci. A une certaine vitesse, les creux de cette vague coïncident avec les sommets de l'oscillation provoquée par la vague d'étrave. Celle-ci est donc annulée.
La longueur d'onde de ces vagues dépend de la vitesse du navire. Par conséquent, le bulbe d'étrave n'est efficace que pour une vitesse donnée. Il permet de gagner jusqu'à 20% environ sur la puissance de propulsion.
Résolution des objectifs
La théorie géométrique élémentaire que nous avons examinée au chapitre précédent est insuffisante pour définir dans leurs plus fins détails les images formées par les objectifs. Ainsi, l'image d'un point lumineux observé avec un fort grossissement n'est pas un point sans dimension. C'est une petite tache entourée d'anneaux faiblement lumineux. Nous pouvons constater ce phénomène sur l'image d'une étoile fournie par un bon télescope qui est illustrée sur la figure 7. C'est le disque de diffraction ou faux disque de l'étoile, on l'appelle aussi disque d'Airy (Sir George Biddell AIRY, 1801 - 1892).
Le disque central n'illustre pas le disque de l'étoile. Ce dernier est tellement petit qu'il n'est jamais perceptible (voir sur une autre page de ce site "la diffraction dans un faisceau limité par une ouverture circulaire".
Un objectif parfait ne donne donc jamais une image qui est une réplique parfaite de l'objet, mais un ensemble de disques d'Airy. Le disque d'Airy constitue la limite de résolution des plus fins détails que peut fournir un objectif.
Avec : λ = longueur d'onde de la lumière considérée Cette relation nous indique qu'un gros télescope fournit des images plus détaillées qu'un petit instrument. Autres caractéristiques de la lumière
La fréquence
Nous avons dit qu'un rayonnement lumineux est un champ électromagnétique oscillant. La fréquence de ce rayonnement est le nombre d'oscillations par seconde de ce champ. C'est une autre façon d'exprimer la longueur d'onde :
Avec : ν = fréquence de la lumière considérée (lettre grecque "nu") Unités de temps et de longueur
La fréquence peut être mesurée avec une grande précision. C'est pour cela que depuis 1967 la définition de la seconde de temps est liée à la fréquence d'un rayonnement électromagnétique. La seconde de temps est la durée de 9 192 631 770 périodes d'un rayonnement particulier émis par le césium 133.
La vitesse de propagation de la lumière est c = 299 792 458 m/s.
Depuis 1983 la définition du mètre est directement liée à la vitesse de la lumière et à la définition de la seconde. Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 de seconde. La couleur
La couleur est une sensation que nous percevons de façon différente selon la longueur d'onde de la lumière que nous voyons. Notre il est sensible aux rayonnements électromagnétiques dont la longueur d'onde est comprise entre 0,4µm et 0,7µm (1µm = 1micromètre = 1 millionième de mètre = 1 millième de millimètre). Entre 0,4 et 0,5µm de longueur d'onde la lumière nous apparaît bleue. Nous percevons du vert entre 0,5 et 0,58µm et du rouge entre 0,58 et 0,7µm (toutes ces longueurs d'onde sont approximatives car elles varient d'un individu à l'autre). Cette perception des couleurs est due à l'existence de trois types de photorécepteurs différents avec lesquels la rétine de notre il perçoit la lumière en vision diurne.
Les sensations de bleu, vert et rouge se composent pour donner toute la gamme des sensations colorées que nous distinguons. Ainsi, suivant la composition de la lumière que nous voyons, nous pourrons percevoir du vert émeraude, du jaune canari ou de l'indigo. Vers 0,58µm les sensations de vert et de rouge s'ajoutent et nous percevons du jaune.
Lorsque la luminosité d'un objet est répartie uniformément dans les trois couleurs bleu, vert et rouge nous le voyons blanc. Ces teintes sont les couleurs primaires. Habituellement, la lumière est un mélange de différentes couleurs. Il existe cependant des cas où on considère une lumière d'une seule longueur d'onde (une seule couleur), c'est le cas de la lumière émise par un laser. Dans ce cas, on dit que la lumière est monochromatique.
Ce que nous venons de décrire signifie aussi que les couleurs n'existent pas en tant que telles dans la nature, ces sensations correspondent seulement à des interprétations de notre cerveau humain. Les autres animaux peuvent avoir des sensations plus ou moins riches que nous dans ce domaine.
Les différents rayonnements électromagnétiques
La lumière visible est une petite partie des rayonnements électromagnétiques. La figure 8 nous montre l'ensemble de ces rayonnements, ils se différencient par leur longueur d'onde. Sur cette image nous avons dilaté le domaine de la lumière visible. Il faut donc retenir que les rayonnements radio, infrarouge, visible, ultraviolet, X et gamma sont des phénomènes de même nature.
Dispersion de la lumière
Nous avons vu qu'un rayon lumineux peut être dévié en traversant un dioptre, c'est la réfraction. Nous devons ajouter que le pouvoir de réfraction d'un corps dépend de la longueur d'onde de la lumière considérée (figure 9). Ceci permet de décomposer la lumière afin de l'analyser, c'est la dispersion chromatique de la lumière.
Ce phénomène de dispersion chromatique est à l'origine de certains défauts des lentilles. En effet, puisque la réfraction varie avec la couleur, une lentille traitera d'une façon différente les rayons de chaque couleur. Sa distance focale ne sera pas la même dans le rouge et le bleu. Les images fournies seront irisées.
Cette caractéristique s'appelle l'aberration chromatique, elle limite la finesse des images obtenues en lumière blanche avec une lentille simple. Elle peut être compensée en grande partie en utilisant des lentilles accolées faites de verres différents.
Un autre principe est utilisé pour disperser la lumière en fonction de sa couleur, c'est la diffraction. Prenons une vitre sur une face de laquelle nous faisons un grand nombre de rayures rectilignes et parallèles. La lumière qui traverse cette vitre rayée est dispersée en fonction de sa couleur, c'est un réseau de diffraction. Le rayonnement thermique
Nos expériences quotidiennes nous permettent fréquemment de constater qu'un rayonnement visible est émis par des objets que l'on chauffe. Un exemple très commun est le filament d'une ampoule à incandescence, il se met à briller quand il est fortement chauffé par un courant électrique.
En analysant ce phénomène, nous constatons que tout corps dont la température absolue n'est pas nulle émet un rayonnement électromagnétique. Pour les températures les plus basses, cette émission est dans le domaine des ondes radioélectriques puis, en montant l'échelle des températures, le maximum de ce rayonnement passe dans l'infrarouge puis dans le visible puis dans l'ultraviolet...
Exemple : une caméra infrarouge peut montrer le rayonnement thermique d'un corps humain ou bien les fuites de chaleur d'une maison.
Rappel : l'échelle des températures absolues commence à 0K (zéro degrés Kelvin) qui équivaut à -273,16°C. Une variation de température de 1K est équivalente à 1°C. Une température ne peut pas être inférieure à 0K.
L'étude de ce rayonnement thermique a mobilisé l'attention de très valeureux physiciens.
Définition du corps noir Le rayonnement thermique d'un corps est fonction de sa capacité d'absorption. C'est pour cela qu'on préfère généraliser les lois du rayonnement thermique à partir de l'étude des propriétés du corps noir.
Un corps noir absorbe tout rayonnement électromagnétique reçu par sa surface. En pratique, on obtient un corps noir en creusant une cavité fermée dans un matériau opaque peu réfléchissant et en perçant un petit trou dans sa paroi. Cet orifice se comporte comme un corps noir.
L'intérieur d'un four constitue une bonne approximation d'un corps noir.
Les photons
Quand des physiciens ont voulu calculer l'énergie totale émise par un corps en employant les lois de la mécanique classique, ils ont obtenu une quantité d'énergie infinie. Ce résultat a été surnommé ironiquement "la catastrophe ultraviolette". Il est bien entendu aberrant et il démontre que la mécanique classique ne décrit pas correctement le rayonnement thermique.
Max Planck était un physicien allemand (Kiel 1858 - Gottingen 1947). En 1900, il a découvert la loi spectrale du rayonnement d'un corps noir.
Pour que sa formule corresponde bien aux données expérimentales, Planck a émis l'hypothèse des quanta dans laquelle il considère que l'énergie lumineuse n'est pas émise de façon continue mais par "grains" dont l'énergie E dépend de la longueur d'onde :
Avec : h = constante de Planck
A l'époque, cette idée était regardée comme un artifice de calcul et personne n'en comprenait vraiment les implications. Aujourd'hui, cette relation de Planck est considérée comme un des fondements de la mécanique quantique.
D'autres physiciens ont étudié cet aspect, notamment Albert Einstein (physicien d'origine allemande 1879-1955) dans son étude de l'effet photoélectrique.
On sait maintenant qu'un faisceau lumineux ne peut pas transporter une quantité quelconque d'énergie, il ne peut pas en transporter moins que ce grain de lumière que l'on appelle photon.
On considère parfois que les photons sont des particules de lumière. Certains parlent même d'une contradiction car la lumière peut tantôt être considérée comme une onde et tantôt comme un ensemble de particules. En fait la nature de la lumière est trop complexe pour être décrite entièrement par une seule de ces deux idées. Rayonnement du corps noir : la loi de Planck Grâce au concept des quanta, Planck a découvert la loi qui définit pour un corps noir la luminance énergétique monochromatique L en fonction de la température :
Avec : h = constante de Planck
Tout corps noir dont la température absolue n'est pas nulle émet un rayonnement radioélectrique selon la loi de Planck.
La loi de Wien Pour une température donnée, la loi de Planck indique un maximum unique.
La loi de Wien donne la position de ce maximum en fonction de la température absolue. Elle a été établie par Wilhelm Wien, un physicien allemand né à Gaffken en 1864 et mort à Munich en 1928, puis elle a été améliorée par Planck.
Voici une expression de la loi de Wien :
Avec : λm = longueur d'onde du maximum de luminance énergétique.
Cette valeur constante s'exprime donc en mètres Kelvin (m.K);
Cette loi confirme ce qui paraît évident en observant la figure 10 : plus la température d'un corps noir est élevée et plus la longueur d'onde du maximum de sa luminance est courte.
En appliquant la loi de Wien à notre Soleil dont la surface a une température de 5770K et en l'assimilant à un corps noir, nous obtenons :
En astronomie, c'est plutôt dans l'autre sens que cette loi est utile. En effet, L'observation spectroscopique des étoiles nous renseigne sur la longueur d'onde du maximum de leur luminance énergétique. Pour obtenir la température absolue de ces astres, il suffit d'appliquer la loi de Wien :
La loi de Stefan-Boltzmann Cette loi relie la puissance rayonnée par un corps noir à sa température absolue. Elle a été découverte expérimentalement en 1879 par Josef STEFAN (physicien autrichien 1838-1893) et établie théoriquement en 1884 par son élève Ludwig Boltzmann (physicien autrichien 1844-1906).
La loi de Stefan-Boltzmann donne la puissance totale M rayonnée par unité de surface du corps noir en fonction de sa température absolue T :
σ est la constante de Stefan-Boltzmann :
Avec : h = constante de Planck
Rayonnement thermique des corps réels Les relations que nous venons d'évoquer concernent le rayonnement thermique du corps noir, c'est à dire un corps parfaitement absorbant. C'est une première approximation quand on veut modéliser le rayonnement thermique d'un objet absorbant voire d'une étoile.
Dans la réalité nous avons affaire à des matériaux plus ou moins absorbants.
Nous allons nommer ε l'émissivité d'un corps. Pour le corps noir ε=1, pour les matériaux réels ε est compris entre 0 et 1 et il dépend de la température et des conditions de mesure.
Si nous considérons cette émissivité, la loi de Stefan-Boltzmann devient :
Prenons le verre, par exemple. Son émissivité est très faible. Par conséquent, il rayonne beaucoup moins qu'un corps noir qui serait porté à la même température.
Loi de Stefan
La puissance totale M rayonnée par un corps noir dans toutes les longueurs d'onde et dans toutes les directions est proportionnelle à sa surface S et à la quatrième puissance de sa température T :
On en déduit que si deux étoiles ont la même température à leur surface, c'est la plus grosse qui rayonne la plus grande puissance.
Si deux étoiles ont le même diamètre, c'est la plus chaude qui rayonne la plus grande puissance.

Ainsi, à chaque instant, nous voyons que le champ électrique E prend une valeur maximale en des lieux régulièrement espacés. La distance entre deux maximums consécutifs est la longueur d'onde.
Lorsque plusieurs rayons lumineux arrivent en même temps sur un même point leurs amplitudes s'additionnent comme l'illustre la figure 4. Les deux rayons A et B (de même amplitude) en se combinant forment l'onde C qui a une amplitude deux fois plus grande.

La figure 5 montre la somme de deux ondes d'amplitudes égales en opposition de phase, c'est à dire que le maximum de l'une intervient en même temps que le minimum de l'autre. Les deux ondes s'annulent mutuellement.




Son rayon est 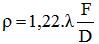
F = distance focale de l'objectif
D = diamètre de l'objectif
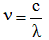
c = célérité de la lumière
λ = longueur d'onde (lettre grecque "lambda")


On l'appelle aussi "radiateur idéal" ou "radiateur de Planck".
E = h.ν
ν = fréquence de la lumière
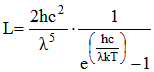
c = célérité de la lumière
λ = longueur d'onde de la lumière
e = base des logarithmes naturels = 2,718281
k = constante de Boltzman
T = température absolue

La courbe pointillée suit la position du maximum de la loi de Planck en fonction de la température, c'est la loi de Wien.
λm.T = 2,897 8.10-3 m.K
T = température absolue
λm Soleil = 2,897 8.10-3 / TSoleil = 2,897 8.10-3 / 5770 = 5.10-7 m = 0,5 µm
Tétoile = 2,897 8.10-3 / λm étoile
M = σ.T4
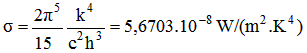
c = célérité de la lumière
k = constante de Boltzman
M = σ.ε.T4
M = σ.S.T4



