Mémento optique

Grossissement d'une lunette ou d'un télescope
Champ d'une lunette ou d'un télescope
Coefficient de déformation d'une surface optique
Coma au foyer du miroir parabolique d'un télescope de Newton
Formules de Descartes
Lentille de Barlow
Distance focale d'une lentille
Distance focale d'un oculaire à 2 lentilles
Achromatisme d'un groupe de lentilles minces accolées
Courbure de champ - Somme de Petzval
Réflexion vitreuse
Rayon de la tache de diffraction
Limite de résolution d'un télescope
Eloignement de l'image par une lame de verre à faces parallèles
Aberration de sphéricité d'une lame de verre à faces parallèles
Equations de Maxwell
Grossissement d'une lunette ou d'un télescope
G est le grossissement d'un instrument :

avec
F = distance focale de l'objectif
f = distance focale de l'oculaire
Exemple : Calculons le grossissement d'un télescope de 900mm de distance focale sur lequel on a monté un oculaire de 20mm de distance focale :
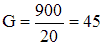
Avec l'oculaire de 20mm, cet instrument grossit donc 45 fois.
Champ d'une lunette ou d'un télescope Ce qui va suivre ne s'applique pas aux lunettes de Galilée.
C est le champ effectif d'un instrument :
avec Exemple : Calculons le champ qui est visible dans un télescope qui grossit 45 fois
avec un oculaire CLAVE dont le champ est de 48° :
Le champ visible dans l'oculaire de cet instrument vaut donc 1,07°. Pour convertir cette valeur en
minutes d'arc, il suffit de la multiplier par 60. On peut donc voir dans cet instrument un champ de 64', c'est à dire 64 minutes d'arc. Coefficient de déformation d'une surface optique :
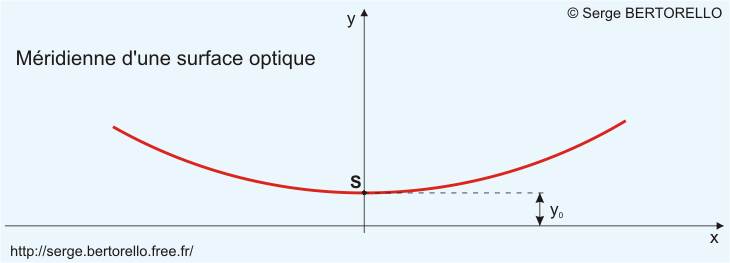
Lors de l'usinage d'une pièce optique de révolution, la forme obtenue naturellement est une portion de sphère dont la méridienne est un cercle. Si l'opticien cherche à obtenir une autre forme, comme par exemple une méridienne parabolique ou elliptique, il déforme la surface sphérique obtenue initialement.
Cet aspect ainsi que le constat que les surfaces optiques sont habituellement très proches de la sphère ont conduit les calculateurs de combinaisons optiques à considérer les méridiennes des surfaces optiques sous forme de développements limités relatifs au cercle. C'est pratique pour le calculateur autant que pour l'usineur.
Dans un repère orthonormé d'axes x et y, la méridienne d'une surface optique est décrite par un développement en fonction des puissances paires de x :
Remplaçons les termes p et q par les éléments connus du miroir :
On néglige généralement le coefficient "c", on ne fait appel à lui que pour des optiques "extrêmes" tels que les grands télescopes.
La plupart du temps, dans les cas qui intéressent l'opticien, les termes d'ordre supérieur à 4 sont négligés car on s'éloigne "peu" de l'axe. C'est pour cela qu'on précise uniquement le coefficient "b".
Avec : y = hauteur du point considéré sur la méridienne La figure ci-dessus montre différentes formes de méridienne. Elle permet de constater que ces silhouettes sont très semblables autour du point où elles sont tangentes les unes aux autres, c'est à dire près de l'axe.
Un coefficient de déformation négatif indique que le rayon de courbure augmente du centre vers le bord.
Coma au foyer du miroir parabolique d'un télescope de Newton :
K est la longueur de l'aigrette de la coma fournie par un objectif de diamètre D à la distance angulaire β de l'axe optique :
avec Les valeurs de K et β doivent être exprimées avec la même unité. Ce sont en principe des valeurs angulaires mais on utilise parfois des valeurs linéaires, c'est une approximation raisonnable.
Nous déduisons donc l'expression suivante qui nous donne la longueur de l'aigrette de coma au foyer du miroir parabolique d'un télescope de Newton :
La coma est extérieure car B est positif.
Exemple : Calculons la dimension de l'aigrette de coma à 20" de l'axe sur l'image fournie par un miroir parabolique de 5080mm de diamètre et de 16963mm de distance focale (c'est le miroir du télescope Hale du Mont Palomar) :
20" c'est approximativement le rayon apparent de la planète Jupiter et 0,33" représente
à peu près la limite de résolution du télescope Hale lorsque les conditions atmosphériques sont
excellentes. Cela signifie que le champ utilisable au maximum de résolution sur cet instrument
ne dépasse pas les dimensions apparentes de Jupiter. Pour obtenir des clichés détaillés sur un champ
plus large (sur la Lune par exemple), il faut employer un correcteur de champ.
Formules de Descartes Ces formules sont très utiles pour les calculs des combinaisons optiques que nous rencontrons
souvent en astronomie. Elles sont applicables dans les conditions d'approximation de Gauss.
Examinons la figure suivante. Un objet est symbolisé par une flèche AB, une lentille forme son
image en A'B'.
Première formule de DESCARTES pour le calcul de la position de l'image
avec Deuxième formule de DESCARTES pour calculer le grandissement de l'image
g est le grandissement.
Dans un cas fréquemment rencontré en pratique, on souhaite déterminer le grandissement en fonction de la distance p. Pour cela nous pouvons étudier conjointement les deux formules de DESCARTES, nous en déduisons l'équation suivante :
Lentille de Barlow La lentille de Barlow est un dispositif optique divergent imaginé par Peter Barlow (Physicien anglais né le 13 octobre 1776 à Norwich et mort 1er mars 1862 à Woolwich) qui allonge la distance focale de l'objectif. En fait, elle est couramment composée par un doublet (2 lentilles) et parfois par un groupe de 3 lentilles (Barlow apochromatique).
Elle est principalement caractérisée par sa distance focale qui est négative et par le grandissement pour lequel elle a été conçue. On dégrade la qualité des images si on l'emploie pour un grandissement différent.
F est le foyer de l'objectif avec : f = valeur absolue de la distance focale de la lentille de Barlow
Tirage = E
Distance focale d'une lentille R1 et R2 sont les rayons de courbure des deux faces de la lentille faite en verre d'indice n. Un rayon de courbure est positif si le dioptre est convexe vers la lumière incidente, il est négatif si le dioptre est concave (d'autres auteurs peuvent très bien suivre la considération inverse).
Lentille mince : Remarquez qu'on peut déduire de cette formule une approximation intéressante dans le cas d'une lentille plan-convexe en verre ordinaire d'indice de réfraction n=1,5 :
avec R = rayon de courbure de la face convexe
Lentille épaisse : Cette formule est intéressante mais elle n'est pas applicable quand les rayons de courbure sont égaux. En effet, dans ce cas, elle nous fait affronter une division par zéro dont le calcul est impossible.
C'est pour cela que je vous propose une deuxième relation qui ne souffre pas de cette limitation :
Distance focale d'un oculaire à 2 lentilles f et f ' sont les distances focales des 2 lentilles qui sont séparées par la distance e.
La formule suivante nous donne la distance focale F de l'oculaire :
L'oculaire de Huygens peut être représenté par la suite 2-3-4, ces chiffres désignent respectivement les proportions entre la distance focale de la lentille d'il, la distance qui sépare les deux lentilles et la distance focale de la lentille de champ. Ainsi, si on prend une lentille d'il de 1cm de focale, on devra prendre une lentille de champ de 2cm de focale avec entre elles une distance de 1,5cm. Voici les formules des oculaires classiques à deux lentilles :
Huygens : 2-3-4
Sur une autre page, vous trouverez la démonstration du calcul qui conduit à cette expression de la distance focale d'un groupe de 2 lentilles.
Achromatisme d'un groupe de lentilles minces accolées La condition d'achromatisme pour un groupe de n lentilles minces accolées s'exprime sous la forme suivante :
Avec : La constringence ν caractérise la dispersion chromatique d'un matériau réfringent. Elle est aussi appelé nombre d'Abbe ou encore coefficient de dispersion d'un verre optique : Avec :
Pour un doublet (c'est à dire deux lentilles minces accolées) la condition de chromatisme devient :
que l'on peut aussi écrire sous la forme suivante :
Pour un triplet apochromatique, cette condition devient :
Courbure de champ - Somme de Petzval Joseph PETZVAL (physicien hongrois né en 1807 à Szepesbéla en Hongrie et mort en 1891 à Vienne en Autriche) a établi une formule qui définit la courbure de champ d'un ensemble de lentilles. On la nomme "la somme de Petzval" :
Avec : Rp = rayon de courbure du champ
Afin d'obtenir la planéité du champ, l'opticien cherche à obtenir une somme de Petzval nulle.
Réflexion vitreuse Considérons un dioptre qui sépare un milieu d'indice de réfraction n1 et un milieu d'indice n2. La formule suivante exprime la proportion de cette réflexion vitreuse pour une incidence normale (c'est à dire perpendiculaire au dioptre) en fonction des indices de réfraction : Dans le cas d'un dioptre air-verre, cette formule prend la forme suivante :
Exemple : Calculons le taux de réflexion de chaque face d'une lentille faite en verre
d'indice de réfraction n = 1,5.
Cela signifie que chaque face d'une lentille de verre réfléchit 4% de la lumière incidente.
Par conséquent, on peut dire qu'un dioptre ne transmet que 96% du flux incident (0,96) à cause de la réflexion vitreuse.
Une lentille simple (comme un oculaire de Kepler) possède deux dioptres et donc elle transmet seulement Et le cas s'aggrave avec d'autres dispositifs. Ainsi des oculaires à deux éléments (Huygens, Ramsden, orthoscopique, Plössl, ...) transmettent seulement 0,964 = 0,85, c'est à dire 85% de la lumière incidente.
Avec un oculaire de Nagler 2 qui comprend 10 surfaces air-verre, on ne récolte plus que 0,9610 = 0,66 (ou 66%) de la lumière incidente. Cela veut aussi dire que 34% de cette lumière incidente est dispersée sous forme d'une lumière parasite dont une partie va immanquablement parvenir dans l'il de l'observateur.
C'est pour atténuer ce phénomène qu'on dépose le plus souvent possible un traitement antireflet sur la surface des lentilles. Avec un traitement antireflet simple, l'amplitude de la réflexion vitreuse est divisée par 4 environ. Avec un traitement antireflet multicouche on peut la diviser par 40 environ.
Rayon de la tache de diffraction Considérons un objectif de diamètre D et de distance focale f qui est dirigé vers une source lumineuse ponctuelle infiniment éloignée (une étoile). L'image qu'il fournit de cette source est une tache de diffraction auréolée avec quelques anneaux.
La formule suivante permet de calculer directement la valeur de ρ en secondes d'arc pour λ=0,56μm. Exemple : Calculons le rayon de la tache de diffraction fournie par un télescope pour lequel
D=200mm, f=1000mm avec λ=0,56μm.
Limite de résolution d'un télescope Dans des conditions d'observation télescopiques parfaites, on considère habituellement qu'on peut
séparer deux étoiles de même éclat écartées de 0,85 rayon de la tache de diffraction (λ=0,56µm).
Un objectif de télescope de 120mm de diamètre peut ainsi séparer deux étoiles distantes
de 1 seconde d'arc. Dans une autre page de ce site consacrée à la diffraction de la lumière, je vous propose un exposé plus détaillé sur le pouvoir séparateur des instruments d'observation.
Exemple : Calculons la limite de résolution d'un télescope de 200mm de diamètre.
Eloignement de l'image par une lame de verre à faces parallèles Si on place une lame de verre à faces parallèles d'épaisseur "e" dans un faisceau lumineux convergent (système centré, optique paraxiale), elle décale le foyer en l'éloignant de l'objectif de la longueur "L" :
Ce décalage est donc fonction de l'indice de réfraction qui dépend lui-même de la longueur d'onde de la lumière. Par conséquent, la traversée de cette lame introduit une aberration chromatique du type sur-correction. Cette expression signifie que c'est le foyer pour les courtes longueurs d'ondes qui est le plus "repoussé" de l'objectif.
L'utilisation de cette formule est souvent nécessaire quand on introduit un filtre dans un faisceau convergent ou quand on calcule un système optique comprenant un prisme à réflexion totale. En effet, pour un faisceau de lumière convergent, la traversée d'un tel élément est équivalente à la traversée d'une lame à face parallèle.
La figure suivante nous montre deux parcours possibles pour l'axe optique d'un faisceau lumineux convergent qui est dévié par un prisme à réflexion totale.
Dans la figure du milieu, l'épaisseur de la lame de verre équivalente est égale à la longueur du petit côté du prisme.
Pour le cas illustré à droite, cette épaisseur vaut la longueur de l'hypoténuse du prisme (le plus grand côté).
Exemple : Calculons le recul du foyer d'un télescope consécutif à la mise en place, avant le foyer, d'un filtre de verre de 3mm d'épaisseur avec n=1,5.
Ce résultat n'est donc pas négligeable et il faudra refaire la mise au point après avoir introduit le filtre.
Aberration de sphéricité d'une lame de verre à faces parallèles En disposant une lame de verre à faces parallèles dans un faisceau lumineux convergent, on introduit une aberration de sphéricité du type sur-correction. Ceci signifie que le foyer des rayons périphériques sera plus éloigné de l'objectif que le foyer des rayons centraux. Δp est l'aberration longitudinale introduite par la lame d'épaisseur "e".
avec : m = rapport d'ouverture (= F/D dans le cas d'un télescope).
Exemple : Pour m=5, n=1,5 e=100mm
Δp=0,185mm
Equations de Maxwell James Clerk Maxwell était un physicien écossais (1831-1879) qui a unifié les théories de l'électricité et du magnétisme en donnant les équations générales du champ électromagnétique.
Les équations de Maxwell réunissent les lois de l'électricité et du magnétisme en une théorie complète. Elles peuvent être résumées par quatre simples équations vectorielles.
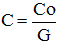
Co = champ de l'oculaire
G = grossissement de l'instrument
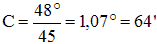
Remarquons que le soleil et la lune pourront être visibles entièrement dans ce champ car leur diamètre apparent est inférieur, il vaut environ un demi degré, c'est à dire 30 minutes d'arc.
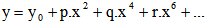
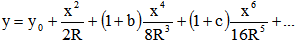
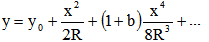
x = distance à l'axe optique
R = Rayon de courbure de la surface
b = coefficient de déformation
Pour la sphère (ou le cercle) : b = 0
Pour la parabole : b = -1
Pour une hyperbole : b < -1
Pour une ellipse autour du grand axe : -1 < b < 0
Pour une ellipse autour du petit axe : b >0
c = second coefficient de déformation

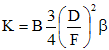
B = coefficient de coma de l'objectif
F = distance focale de l'objectif
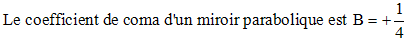
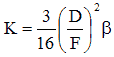
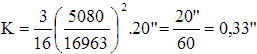

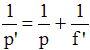
p = distance entre l'objet et la lentille
p' = distance entre la lentille et l'image
f' = distance focale de la lentille
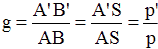
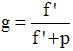
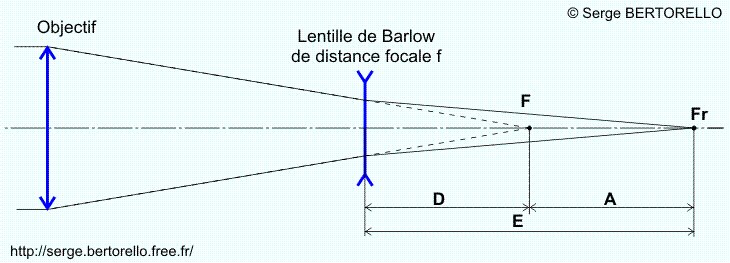
Fr est le foyer résultant
Grandissement = G


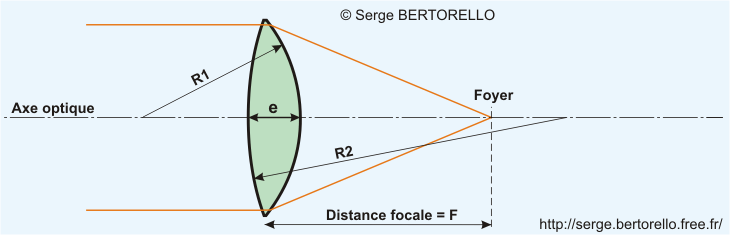
En négligeant l'épaisseur de la lentille, on obtient la formule suivante :
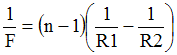
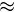 2.R
2.R
En considérant l'épaisseur e de la lentille, on obtient la formule suivante :
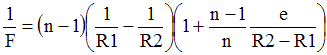
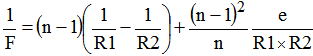

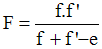
Dollond : 1-2-3
Ramsden : 3-2-3
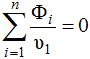
Φi = puissance optique de la lentille i
νi = constringence du verre composant la lentille i
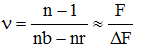
n = indice de réfraction pour le vert
nr = indice de réfraction pour le rouge
nb = indice de réfraction pour le bleu
F = distance focale de la lentille
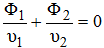

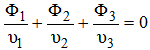
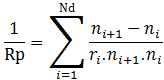
Nd = nombre de dioptres
ri = rayon de courbure du dioptre i
ni = indice de réfraction du dioptre i
Un faisceau incident sur ce dioptre sera partiellement réfléchi.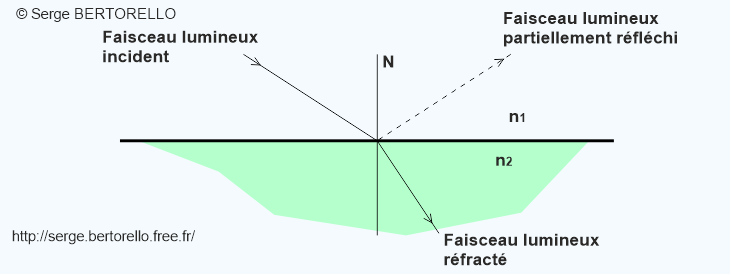
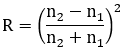
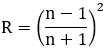
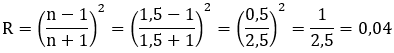
0,96 x 0,96 = 0,92 (ou 92%) du flux lumineux incident.
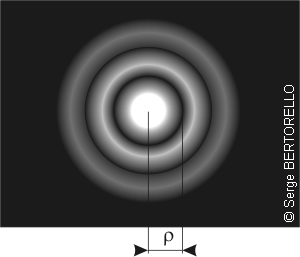
ρ est le rayon de cette tache de diffraction et λ est la longueur d'onde de la lumière considérée.
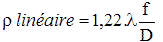
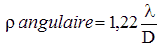
Ce résultat est exprimé en radians.
D doit être exprimé en millimètres.
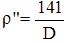
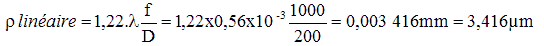
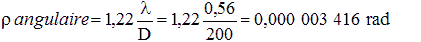
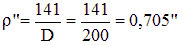
La limite de résolution p (en secondes d'arc) d'un télescope de diamètre D (en millimètres)
est donnée par la relation :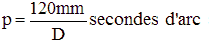
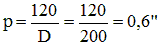
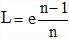

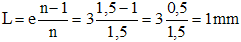
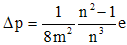
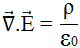 |
(Divergence de E à travers une surface fermée) = (charge intérieure) / εo
Equation qui décrit comment le champ électrique est généré par des charges électriques. |
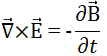 |
(Rotationnel de E le long d'une courbe fermée) = - d/dt (flux de B à travers la courbe)
La variation du champ magnétique créé un champ électrique |
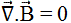 |
(Divergence de B à travers une surface fermée) = 0
Par conséquent, il ne peut exister de monopôle magnétique. |
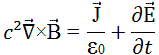 |
c2(Rotationnel de B le long d'une courbe fermée) = (courant à travers la boucle) / εo + d/dt (flux de E à travers la courbe) |
Le signe ∇ désigne l'opérateur nabla :
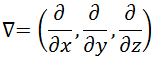 |

