NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
Calcul des combinaisons optiques
Optique paraxiale
Conditions de Gauss
Les méthodes de calcul des combinaisons optiques que nous allons étudier sont en principe limitées aux lentilles minces (c'est à dire dont l'épaisseur est négligeable) et aux faisceaux lumineux peu écartés de l'axe et dont l'angle d'ouverture est inférieur à 3°. Les rayons lumineux sont dits paraxiaux.
Ce sont les conditions d'approximation de Gauss (Carl Friedrich GAUSS, 1777 - 1855).
En pratique, la précision des calculs sera d'autant plus altérée que l'on s'écartera de ces limites.
Dans ce chapitre nous considèrerons des systèmes optiques centrés. Un système de lentilles sphériques est dit centré lorsque les centres de courbure des différents dioptres qui composent les lentilles sont alignés sur une droite appelée axe optique du système.
Conventions
La figure 1 illustre les conventions que nous allons utiliser. Elle représente une lentille convergente. Celle-ci comporte deux foyers.

- F est le foyer côté objet, nous l'appellerons foyer objet.
f est la distance focale objet.
F' est le foyer image.
f' est la distance focale image.
S est le centre de la lentille.
Détermination graphique
Examinons la figure 2. Un objet est symbolisé par une flèche AB, une lentille forme son image en A'B'.

Déterminons la position et la taille de cette image.
Pour cela nous pouvons utiliser deux des trois rayons particuliers suivants :
- Le rayon incident BI parallèle à l'axe, qui émerge suivant IF'. En effet, nous avons vu qu'un rayon incident parallèle à l'axe sort de la lentille en passant par le foyer image F'.
- Le rayon incident BF, qui émerge parallèlement à l'axe puisqu'il passe par le foyer objet F. C'est le cas symétrique du précédent.
- Le rayon incident BS, qui n'est pas dévié car il passe par le centre S de la lentille.
Cette méthode graphique nous permettra donc de concevoir très simplement des combinaisons optiques destinées à former des images.
Nous pouvons aussi déterminer la position de l'image par le calcul. Pour cela René Descartes (1596 - 1650) a démontré la formule suivante :

avec : p = distance entre l'objet et la lentille
p' = distance entre la lentille et l'image
f ' = distance focale de la lentille
Méthode graphique
La construction graphique de la figure 2 nous donne directement la taille de l'image, à condition de connaître l'échelle du schéma.
En analysant la figure 2 nous constatons que les triangles ABS et A'B'S sont semblables. Par conséquent nous pouvons énoncer l'équation suivante :

g est le grandissement.
C'est la deuxième formule de DESCARTES.
Le cas de l'objectif du microscope correspond à la figure 2 avec une petite distance p et une grande distance p'. Ainsi le grandissement est important.
Dans un cas fréquemment rencontré en pratique, on souhaite déterminer le grandissement en fonction de la distance p. Pour cela nous pouvons étudier conjointement les deux formules de DESCARTES, nous en déduisons l'équation suivante :

Quelques exemples
Examinons la figure 3.

Elle représente le cas de l'objectif de la lunette astronomique ou de l'objectif photographique quand l'objet est situé sur l'axe à une distance très grande par rapport à la longueur focale.
Dans ce cas l'image de l'objet est très petite, les points A' et B' sont confondus avec le foyer image F'.
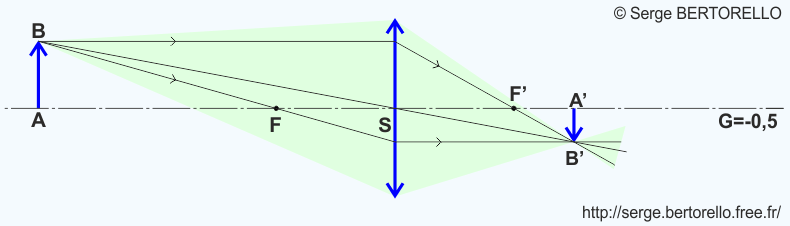
Si nous rapprochons cet objet jusqu'à une distance égale à trois fois la distance focale, nous obtenons le cas de la figure 4 où

La première formule de DESCARTES nous indique donc :

La deuxième formule nous donne le grandissement :

L'image est deux fois plus petite que l'objet et elle est renversée. Ce dernier point est indiqué par le signe négatif du grandissement.
Considérons maintenant le cas particulier de la figure 5.

La distance de la lentille à l'objet vaut le double de la distance focale.

Dans ce cas la distance entre la lentille et l'image a la même valeur (au signe près).

Le grandissement est unitaire.

L'image a la même taille que l'objet mais elle est encore inversée.
L'exemple suivant montre une lentille de Barlow montée derrière un objectif. La lentille de Barlow est un dispositif optique divergent imaginé par Peter Barlow (Physicien anglais né le 13 octobre 1776 à Norwich et mort 1er mars 1862 à Woolwich) qui allonge la distance focale de l'objectif (voir aussi le mémento optique).

Nous allons déterminer graphiquement la position du foyer résultant.
Prenons tout d'abord le rayon lumineux qui passe par le centre de la lentille de Barlow et par l'extrémité de l'image fournie par l'objectif seul à son foyer F, il est tracé en bleu. Ce rayon n'est pas dévié par la seconde lentille.
Etudions maintenant le rayon parallèle à l'axe qui participe à l'image primaire du même point, il est coloré en orange. Sa traversée de la lentille de Barlow le réfracte de telle sorte qu'il semble provenir du foyer objet de cette lentille Fo. A partir de là, nous l'avons coloré en rouge.
L'intersection de ces deux rayons (bleu et rouge) indique la position de l'image résultante, c'est à dire du foyer résultant.
Ce dessin nous permet aussi de déterminer graphiquement la taille de l'image que la lentille de Barlow a agrandi dans un rapport G = E /D
Dans certains cas, la lumière converge après sa sortie du système optique et elle peut former une image sur un écran, on dit que cette image est réelle.
Notez que cet écran peut être remplacé par une surface sensible afin d'enregistrer une photographie.
Dans d'autres cas, les rayons sortent du système en divergeant et semblent provenir d'une image située avant la sortie du système optique. Celle-ci ne peut donc pas se former sur un écran et on dit que cette image est virtuelle.
Il existe aussi des cas où un faisceau convergent est interrompu par un élément optique avant d'avoir formé une image réelle. Cette image est aussi qualifiée de virtuelle car elle n'est jamais vraiment formée.
Observons les illustrations de la figure 7.

Dans le cas [a], la lentille L forme une image réelle A' de l'objet réel A.
Dans le cas [b], la lentille L forme une image virtuelle A' de l'objet réel A.
Dans le cas [c], la lentille L forme une image réelle A" de l'objet virtuel A'.
Dans le cas [d], la lentille divergente L forme une image virtuelle A" de l'objet virtuel A'.
Les conventions graphiques que nous venons d'étudier peuvent aussi être employées avec les miroirs.
La figure 8 illustre un exemple de formation d'une image par un miroir convergent (miroir concave).

Remarquez la trajectoire des rayons particuliers qui ont permis la construction du graphique :
- Le rayon issu de B parallèlement à l'axe optique se réfléchit sur le miroir selon une direction qui passe par le foyer F.
- - Le rayon issu de B qui passe par le centre M du miroir est réfléchi selon une direction symétrique par rapport à l'axe optique.
- - Le rayon qui part de B vers le foyer F est ensuite réfléchi selon une direction parallèle à l'axe optique.
Nous constatons que les rayons réfléchis convergent au point B' qui est donc l'image de B.
La figure suivante illustre le schéma conventionnel pour un miroir divergent (miroir convexe).

Ainsi, on peut extrapoler pour les miroirs l'ensemble des aspects que nous avons de considérés pour les lentilles.
Le schéma obtenu avec un miroir est semblable au schéma employé avec une lentille. Tout se passe comme si la feuille sur laquelle on a tracé les rayons destinés à une lentille était repliée au niveau de la lentille. Remarquons toutefois, que le schéma d'un miroir est moins clair que celui d'une lentille. C'est pour cela que je remplace souvent les miroirs par des lentilles dans mes schémas. Je pense que c'est beaucoup plus efficace dans certains cas.
Approximation dans les calculs d'optique
Dans ce chapitre, nous n'avons pas considéré les défauts dont peuvent être affectées les images. Ces imperfections de conception se nomment aberrations (nous ne considérons pas les défauts de fabrication).
Ces aberrations peuvent être décrites par un développement limité en fonction du rayon de l'objectif, du diamètre du champ et de la distance angulaire à l'axe (azimut). Il s'agit d'un polynôme dont les termes sont en progression croissante des puissances de ces paramètres. La classe d'approximation est définie par l'exposant maximal qui est pris en compte.
Aberrations du premier ordre : Ce sont les aberrations qui sont proportionnelles au rayon de l'objectif. Ce sont les erreurs par rapport à l'optique gaussienne (optique paraxiale). Il s'agit d'une part des décalages des points images par rapport à la position nominale gaussienne (erreur d'échelle) et d'autre part d'un défaut de mise au point (défocalisation).
Aberrations du troisième ordre : Ce sont les aberrations définies par les termes comprenant le rayon de l'objectif dont la puissance est inférieure ou égale à 3. Nous les examinerons dans un autre chapitre (voir "Les aberrations").

