NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
Il convient à présent de se familiariser avec la notion d'aberration.
On parle d'aberration quand une partie des rayons lumineux qui forment l'image d'un point (ou une étoile) sont dirigés à l'extérieur de la tache d'Airy. Nous examinerons ici les défauts des images dus à la conception des instruments et non pas les défauts de fabrication.
On classe ces imperfections parmi six aberrations fondamentales. Il s'agit de l'aberration chromatique que nous venons d'étudier et des cinq aberrations géométriques élémentaires du troisième ordre. Cette dernière expression désigne le niveau d'approximation des calculs.
L'aberration de sphéricité : Les faces d'une lentille usuelle ont la forme d'une portion de sphère car c'est la forme la plus facile à obtenir. Pourtant, afin d'obtenir une image nette, il est parfois nécessaire que la lentille ait un autre profil (elliptique, parabolique, hyperbolique...). Ce défaut de la forme de la lentille provoque un manque de netteté sur toute l'image, c'est l'aberration de sphéricité.
On parle de cette aberration quand les rayons lumineux qui passent par le bord de l'objectif forment une image en avant ou en arrière de celle qui est composée par les rayons proches de l'axe. Les rayons centraux et les rayons marginaux ne convergent pas à la même distance de l'objectif.
Dans la formulation mathématique qui caractérise les aberrations d'un système optique, l'aberration de sphéricité est constituée par les termes qui sont indépendants de la distance à l'axe et de la couleur de la lumière.
Dans ce qui suit, nous considérons que l'objet observé est infiniment éloigné, son image se forme donc
au foyer du dispositif.
L'aberration longitudinale des rayons marginaux est la distance L'image d'une étoile obtenue avec une lentille simple est une tache dont le rayon au niveau du foyer s'appelle "aberration Transversale des rayons marginaux", c'est la distance La tache de moindre aberration a un rayon 4 fois plus petit, elle est positionnée au niveau du point G, lui-même situé aux 3/4 de la distance de FO à FH.
Le coefficient d'aberration de sphéricité caractérise le dispositif optique étudié. Pour une lentille simple, il dépend notamment de sa cambrure et de son épaisseur. Avec une lentille simple en verre d'indice n=1,5 utilisée comme objectif et un objet à l'infini, la plus faible valeur du coefficient de sphéricité vaut environ 1. Il correspond à une lentille qui est presque plan-convexe avec la convexité dirigée vers l'objet.
Les formules ci-dessus montrent notamment que l'influence de l'aberration de sphéricité diminue quand on augmente la distance focale. Les "grandes lunettes" des pionniers souffraient donc peu de cette aberration.
Une façon de corriger l'aberration de sphéricité consiste à utiliser des dioptres "asphériques" mais ils peuvent être difficiles à réaliser. Une autre méthode consiste à compenser l'aberration de sphéricité d'une lentille par l'aberration d'une autre. Nous avons vu qu'un objectif achromatique est un doublet, c'est à dire qu'il est composé de deux lentilles. Lors de la conception, on annule l'aberration de sphéricité de l'objectif en choisissant des formes de lentilles dont les aberrations de sphéricité sont de mêmes valeurs et de signes opposés.
Il est parfois utile de savoir qu'une lame de verre à faces parallèles placée dans un faisceau lumineux convergent (exemple : entre l'objectif et l'image) introduit une aberration de sphéricité (Voir dans notre formulaire : L'aberration de sphéricité d'une lame de verre à faces parallèles).
Les aberrations que nous venons d'évoquer altèrent l'image sur toute son étendue. Nous allons étudier maintenant des aberrations qui se manifestent en dehors de l'axe optique.
La coma : Considérons un instrument d'observation qui est corrigé des aberrations précédentes et qui est affecté par la coma. La figure 11 montre des images stellaires obtenues en s'éloignant de l'axe optique. Près de l'axe, cette aigrette de coma modifie la répartition de la luminosité dans la figure d'Airy, puis elle prend une forme triangulaire quand on s'écarte du centre du champ.
La figure 12 montre l'aspect de la coma à plus grande distance de l'axe optique. C'est souvent cette aberration qui limite l'étendue du champ exploitable.
Dans la formulation mathématique qui caractérise les aberrations d'un système optique, la coma est constituée par les termes qui sont proportionnels à la distance à l'axe. L'expression suivante nous donne la longueur K de l'aigrette de la coma obtenue sur l'image d'une étoile avec un objectif de diamètre D à la distance angulaire β de l'axe optique :
avec K et β doivent être exprimés avec la même unité. En principe, ce sont des valeurs angulaires
mais on utilise parfois des valeurs linéaires, c'est une approximation raisonnable.
Selon la constitution de l'objectif, la pointe de cette figure en forme de goutte d'eau peut être dirigée vers l'axe optique (B est positif) ou dans la direction opposée (B est négatif).
On dit qu'un instrument est aplanétique quand il est corrigé simultanément de l'aberration de sphéricité et de la coma.
Les objectifs des lunettes astronomiques sont aujourd'hui des objectifs achromatiques aplanétiques.
C'est cette aberration qui limite le plus souvent l'étendue du champ exploitable dans un instrument d'observation. Il est donc particulièrement intéressant de l'examiner plus en détail.
Considérons un objectif de centre O et de distance focale F qui souffre seulement de la coma, oublions la diffraction et analysons l'image qu'il forme d'une étoile écartée de son axe optique par un angle β.
La pointe de l'image se situe au point Ip, il représente l'image paraxiale. Le reste de cette forme est constitué par un empilement de cercles successivement décalés et alignés sur l'axe qui passe par le foyer f. Chacun de ces cercles de rayon Z(hi) est formé par une zone circulaire i de l'objectif, qui lui est concentrique et qui a un rayon hi. Sur l'image de la coma, chaque cercle est éloigné du point Ip d'une valeur L(hi) égale à deux fois son rayon et par conséquent les deux côtés de la pointe font entre eux un angle de 60°.
Pour calculer la longueur totale K de la coma on considère la zone extérieure de l'objectif de rayon R :
Il s'agit de la coma tangentielle. C'est à celle-ci qu'on fait allusion en l'absence de précision contraire.
Reste à calculer Z(hi) :
B est le coefficient de coma de l'objectif.
Pour calculer la longueur totale K de la coma, nous considérons le rayon R de l'objectif ainsi que son diamètre D, en nous rappelant qu'elle vaut trois fois Z(R) :
D'où nous tirons la formule [7] indiquée précédemment :
Voyons maintenant un autre aspect qui n'apparaît pas dans cette formulation. Pour cela nous disposons un écran opaque devant l'objectif et nous perçons celui-ci à la distance Z(hi) de l'axe optique puis nous le faisons tourner autour de l'axe optique. En procédant ainsi, nous isolons un pinceau lumineux qui participe à la formation de l'image de la coma et nous lui faisons parcourir un cercle autour du centre de l'objectif.
Avec ce montage, nous analysons la coma sur l'image d'une étoile hors de l'axe.
Nous constatons alors qu'une seule rotation du trou autour du centre de l'objectif provoque une rotation de deux tours sur le cercle correspondant dans l'image de la coma.
Encore une remarque, l'image de la coma obtenue avec un télescope est un peu moins longue que la valeur déterminée par les formules ci-dessus. C'est l'obstruction centrale par le miroir secondaire qui en est la cause. En effet, la silhouette du miroir secondaire occulte la partie centrale du miroir principal responsable de la pointe de l'image de la coma. Cette pointe n'est donc pas présente dans l'image formée par un télescope ce qui diminue la longueur totale de la coma et arrondit son extrémité.
L'astigmatisme et la courbure de champ : Considérons une lentille de faible ouverture (grand rapport F/D), les aberrations précédentes seront peu marquées pour celle-ci. Analysons l'image qu'elle donne d'un point distant situé dans une direction très écartée de l'axe optique.
Dans ce qui suit nous considèrerons le plan sagittal, c'est le plan qui comprend la ligne de visée du point objet considéré et l'axe optique de l'objectif (plan de symétrie).
Analysons la concentration du faisceau lumineux le long de l'axe de visée avec un écran. Plaçons tout d'abord cet écran au point FA de la figure 13 qui est le lieu où le faisceau est le plus concentré. Ici, l'image du point est en fait une tache circulaire.
Rapprochons, l'écran de la lentille. Nous voyons alors la tache initiale s'allonger jusqu'à prendre au point T la forme d'un segment de droite perpendiculaire au plan sagittal, c'est la focale tangentielle. La tache forme ensuite une ellipse dont le grand axe est perpendiculaire au plan sagittal.
Eloignons maintenant l'écran de la lentille à partir de FA. La tache s'allonge dans une direction perpendiculaire à la précédente jusqu'à prendre au point S la forme d'un segment de droite orienté dans le plan sagittal, c'est la focale sagittale. La tache forme ensuite une ellipse dont le grand axe est dans le plan sagittal.
Ceci est la manifestation de l'astigmatisme. Notez que l'on peut aussi désigner sous ce terme des imperfections de fabrication que nous ne considérons pas ici.
Les focales sagittale et tangentielle sont séparées par la distance L qui est la "longueur d'astigmatisme". Leurs positions dépendent des caractéristiques de l'objectif.
L'exemple illustré sur la figure 14 montre que ces focales sont situées sur des surfaces courbes dont les sommets sont confondus avec le foyer image de l'objectif. L'image de meilleure netteté (lieux des points FA) réside sur une surface courbe et non pas sur un plan. C'est la "courbure du champ".
L'astigmatisme et la courbure du champ sont donc des concepts étroitement liés. Ces deux aberrations provoquent des défauts de l'image proportionnellement au diamètre de l'optique et au carré de la distance à l'axe.
Les formules suivantes indiquent le diamètre C du cercle de moindre aberration dû à l'astigmatisme ainsi que la longueur d'astigmatisme L à la distance β de l'axe :
Avec : A = coefficient d'astigmatisme de l'objectif de Diamètre D et de distance focale F.
C et β sont exprimés en radians. Joseph PETZVAL (physicien hongrois né en 1807 à Szepesbéla en Hongrie et mort en 1891 à Vienne en Autriche) a établi une formule qui définit la courbure de champ d'un ensemble de lentilles. On la nomme "la somme de Petzval" :
Avec : Rp = rayon de courbure du champ
Afin d'obtenir la planéité du champ, l'opticien cherche à obtenir une somme de Petzval nulle.
Remarque : Il faut prendre garde à ne pas confondre la planéité du champ avec l'aplanétisme que nous avons évoqué plus haut. Ces deux expressions ont des significations tout à fait différentes.
La distorsion : Une image peut être nette en tous points et être déformée, on dit qu'elle a subi une distorsion. Cette aberration est indépendante de l'ouverture de l'instrument. Elle correspond au fait que le grossissement (ou le grandissement) d'une image n'est pas le même au centre et au bord du champ. Sur un cliché astronomique, elle n'est préoccupante que si l'on veut mesurer la position des objets (astrométrie).
Observons l'image d'un carré (Figure 15).
L'illustration de gauche représente l'image du carré sans distorsion.
Celle du centre est affectée par une distorsion en croissant, ici le coefficient de distorsion est positif,
cela signifie que le grandissement est plus grand au bord qu'au centre.
Le dessin de droite montre une distorsion en barillet, le coefficient de distorsion est négatif,
le grandissement est plus faible au bord du champ.
Les reflets : Bien qu'il ne s'agisse pas de ce que l'on appelle une aberration, nous devons aussi être conscients que les réflexions entre les faces des différentes lentilles peuvent créer une lumière parasite qui diminue la luminosité de l'image et altère son contraste.
Voir dans le mémento optique comment on peut calculer la réflexion vitreuse.
Pour pallier à cette dégradation de l'image, on recouvre la surface des lentilles d'un dépôt antireflet.

FO = foyer des rayons centraux, FH = foyer des rayons marginaux,
FG = lieu de la plus petite section du faisceau.
 :
:
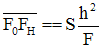 [5]
[5]
Avec :
S = Coefficient de l'aberration de sphéricité
h = Hauteur d'incidence
F = Distance focale du dispositif
 :
:
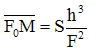 [6]
[6]


 [7]
[7]
B = coefficient de coma de l'objectif
F = distance focale de l'objectif

L(hi) = 2.Z(hi)
K = Z(R) + L(R) = 3.Z(R)





 [8]
[8]
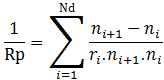
Nd = nombre de dioptres
ri = rayon de courbure du dioptre i
ni = indice de réfraction du dioptre i


