NOTIONS D'OPTIQUE

POUR LES ASTRONOMES AMATEURS

L'objectif de la lunette astronomique

Les premières lunettes d'approche construites selon la formule de Galilée ou selon celle de Kepler possédaient une lentille simple en guise d'objectif, ceci limitait sensiblement les performances car les images étaient irisées. En effet, l'image d'une étoile fournie par une telle lentille est entourée d'une auréole colorée causée par l'aberration chromatique.

En optique, le mot "aberration" désigne une imperfection d'un système optique qui dégrade l'image qu'il produit.

Nous avons vu précédemment que la lumière est déviée lorsqu'elle traverse un prisme de verre. En fait, cette déviation dépend de la couleur de la lumière car le verre ne dévie pas pareillement les rayons lumineux de longueurs d'ondes différentes. L'aberration chromatique d'une lentille est provoquée par cette dispersion chromatique du verre dont elle est composée. Les figures suivantes illustrent la dispersion chromatique d'un prisme en verre (figure 5) et sa conséquence sur une lentille constituée du même matériau (figure 6).

Figure 5 : La dispersion chromatique d'un prisme de verre.

Figure 6 : La dispersion chromatique d'une lentille en verre.

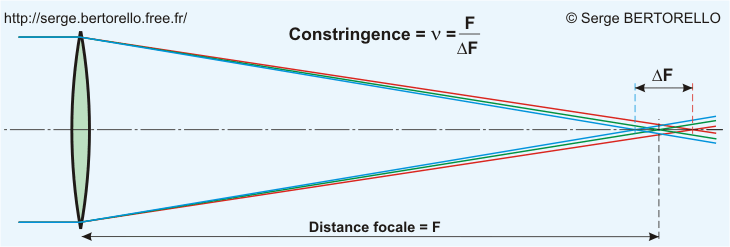
A cause de l'aberration chromatique, la longueur focale d'une lentille de verre est plus courte pour la lumière bleue et plus longue pour la lumière rouge. Ainsi, quand l'image est nette pour une couleur donnée, elle est floue pour les autres couleurs.

La constringence ν (lettre grecque "nu") caractérise la dispersion chromatique du matériau réfringent:

     [1]

Avec :
     n = indice de réfraction pour le vert
     nr = indice de réfraction pour le rouge
     nb = indice de réfraction pour le bleu

Pour être précis, il faut indiquer les longueurs d'onde qui correspondent aux indices de réfraction choisis. Usuellement on choisit pour le vert la longueur d'onde "d" de la raie jaune de l'hélium (587,5618nm) ou la longueur d'onde "e" de la raie verte du mercure (546,0740nm). Pour le rouge, il est courant de prendre l'indice de réfraction pour la raie "C" de l'hydrogène (656,2725nm) et pour le bleu celui de la raie "F" de l'hydrogène (486,1327nm).

La valeur de la constringence dépend donc du domaine spectral considéré. Dans ce qui va suivre, nous considèrerons le domaine de la lumière visible.

Ce nombre ν est aussi appelé nombre d'Abbe ou encore coefficient de dispersion d'un verre optique.

Le verre employé par les premiers constructeurs de lunettes avait sensiblement les caractéristiques suivantes :
        n = 1,52
        ν = 62

Il s'agissait du verre crown, ce qui signifie "couronne" en anglais. Ce nom rappelle l'aspect de la galette de verre en fusion lors d'une étape de la fabrication.

Si nous dirigeons une lentille simple convergente vers une étoile, nous désirons qu'elle concentre la lumière sur un point qui représente l'image de cet astre. En fait, à cause de l'aberration chromatique, l'image obtenue est une tache dont le rayon "r" est indépendant de la distance focale.

     [2]

Avec : D = diamètre de la lentille

Une lentille simple de 100mm de diamètre ne peut donc pas fournir, à cause de son aberration chromatique, une image stellaire de moins de 0,4 mm de rayon.

Les opticiens du 17^ième siècle avaient compris qu'ils pouvaient atténuer les conséquences de cette aberration chromatique des lunettes en donnant une grande distance focale à la lentille-objectif. En effet, en allongeant cette distance focale on augmente la taille de l'image sans influencer la dimension des défauts dus à l'aberration chromatique.

Figure 7 : Image d'une étoile.

Si les rayons lumineux respectaient strictement les règles géométriques que nous avons examinées jusque-là et si les instruments d'observation étaient idéalement parfaits, ces derniers fourniraient des images infiniment détaillées. En agrandissant celles-ci, on obtiendrait toujours plus de détails. En fait, la nature ondulatoire de la lumière impose une limite à la finesse des détails fournis par un objectif. A cause des phénomènes de diffraction, l'image d'un point lumineux est étalée sur une tache ronde. C'est le disque d'Airy qui est entouré d'anneaux concentriques faiblement lumineux et d'intensité décroissante.
Il tient son nom de Sir George Biddell AIRY (1801 - 1892).

La figure 7 montre l'image d'une étoile fournie par un bon objectif. L'image obtenue avec un objectif parfait n'est donc pas une réplique parfaite de l'objet, mais un ensemble de disques d'Airy (voir sur une autre page de ce site "la diffraction dans un faisceau limité par une ouverture circulaire").

L'image d'une étoile obtenue avec un objectif parfait de 100mm de diamètre et 1000mm de distance focale est un disque d'Airy de 6,8µm de rayon. Rapporté sur la voûte céleste, cela correspond à une dimension angulaire de 1,4 seconde d'arc.

Avec un bon instrument employé pour l'observation visuelle, un observateur perçoit au mieux les deux premiers anneaux de diffraction de l'image d'Airy mais théoriquement il y en a un nombre infini.

Les aberrations et les défauts d'usinage des pièces optiques peuvent provoquer l'augmentation de luminosité des anneaux de diffraction. Percevoir de nombreux anneaux de diffraction autour de l'image d'une étoile ne présage donc pas une bonne qualité optique de l'instrument d'observation.

Voir dans le mémento optique le calcul du rayon de la tache de diffraction.

Si on voulait réaliser avec une lentille simple de 100mm de diamètre un objectif dont la tache d'aberration chromatique soit d'une taille comparable à la tache de diffraction, il faudrait lui donner une longueur focale d'environ 19m. Pour satisfaire à ce critère, un objectif de 20cm de diamètre devrait avoir une distance focale de 75m.

Il faudrait encore doubler (au moins) la longueur focale pour que l'aberration chromatique commence à devenir imperceptible.

C'est pour cela que des "longues lunettes à faire peur aux gens" sont apparues au 17^ième siècle (selon l'expression de Molière <1622-1673> dans sa pièce "Les Femmes savantes" de 1672). C'était toutefois une solution insatisfaisante car elle conduisait à la réalisation d'instruments peu maniables.

Figure 8 : Hévélius construisit sa grande lunette de 150 pieds (49m de distance focale) avec un tube ouvert. La lumière parasite était éliminée par des diaphragmes. Gravure publiée en 1673.

Figure 9 : Deux objectifs achromatiques vus en coupe.
Cliquer sur l'image pour obtenir les caractéristiques détaillées d'un objectif achromatique aplanétique.

Le verre flint doit son nom à l'ancien procédé de fabrication qui utilise du silex pur (En anglais, "flint" signifie "silex").

Pour que l'objectif soit achromatique, il faut que la dispersion chromatique de la lentille divergente en flint compense exactement celle de la lentille convergente en crown. Pour cela, elles doivent satisfaire à la condition suivante :

     [3]

Φ₁ et Φ₂ sont les puissances optiques des deux lentilles, ν₁ et ν₂ sont leurs constringences respectives.

Le signe négatif indique qu'une des deux lentilles est divergente, elle a une puissance négative.

La puissance optique Φ du doublet est simplement la somme des puissances de chacune des deux lentilles :

Φ = Φ₁ + Φ₂     [4]

La lentille divergente a une puissance optique inférieure à celle de la convergente (en valeur absolue) car son verre est plus dispersif. Il existe une infinité de configurations qui satisfont à cette condition mais les aspects pratiques orientent le choix de l'opticien.

On peut, par exemple, adapter les courbures des lentilles pour que celles-ci puissent être collées. Cette solution est souvent adoptée pour les petits instruments destinés à un usage terrestre (longues vues, jumelles...).

On peut aussi rechercher la combinaison de ces lentilles qui fournit la meilleure qualité de l'image en dehors de l'axe. Cette démarche a conduit à définir l'objectif aplanétique qui est maintenant employé systématiquement pour les lunettes astronomiques. Dans ce cas, les deux lentilles sont séparées par un faible espace d'air et elles ne peuvent pas être collées car les courbures en vis-à-vis ne sont pas identiques.

Pour un instrument donné, l'aberration chromatique n'est pas la même selon qu'il est utilisé pour la vision, pour la photographie, pour un capteur CCD, etc. Il faut donc définir le domaine spectral que l'on considère.

Nous avons évoqué plus haut qu'il reste un chromatisme résiduel car les propriétés spectrales des deux lentilles d'un objectif ne sont jamais parfaitement complémentaires. Pour limiter son effet, on donne une longue distance focale aux objectifs de lunettes astronomiques (souvent F/D=15).

Pour réduire ce chromatisme résiduel, l'usage a consacré trois méthodes qui sont caractérisées par des prix de revient élevés :

- Verres à très faible dispersion : En utilisant un verre à très faible dispersion chromatique (exemple : fluorite), on peut obtenir un objectif achromatique avec des lentilles aux courbures faibles compatibles avec les petits rapports F/D mais ce matériau est coûteux.
Voir un exemple d'objectif fluorite.

- Objectif semi-apochromatique : On conçoit un objectif de ce type en choisissant soigneusement le couple de verres afin de minimiser l'aberration chromatique résiduelle. Je ne connais pas de définition rigoureuse de ce type d'objectif et je considère qu'il s'agit d'une distinction commerciale pour des objectifs achromatiques...

- Objectif apochromatique : Un objectif achromatique fait coïncider les foyers de deux longueurs d'onde alors qu'un objectif apochromatique fait coïncider les foyers pour trois longueurs d'onde. Ceci atténue fortement le chromatisme résiduel. Généralement pour cela on conçoit un objectif avec trois lentilles.
Voir un exemple d'apochromat à trois lentilles et un autre exemple à 5 lentilles.