NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
La formation des images
Expérience
Le plus simple appareil destiné à projeter une image est... un trou!
Considérons le montage de la figure 1. Il s'agit d'un tube en carton d'environ 20cm de long comme celui qui est au centre d'un rouleau de SOPALIN. Une extrémité est obturée par un bout de papier calque (papier transparent) et l'autre par un carton percé d'un trou d'aiguille de 1mm de diamètre environ.

Plaçons une ampoule électrique à incandescence à verre clair devant le trou (figure 2). Mettons-la sous tension.

Lorsque notre tube est dirigé vers la lampe, nous pouvons voir se former une image de l'ampoule sur le papier calque. Cette silhouette est très pâle et c'est surtout l'image du filament incandescent que l'on remarque.
Faisons les constatations qui s'imposent.
- - L'image est renversée de bas en haut et de droite à gauche.
- Elle est floue et peu lumineuse.
- Si nous agrandissons le trou, l'image devient plus lumineuse et plus floue.
- Plus l'ampoule est éloignée du trou, plus son image est petite.
- Si nous faisons varier la longueur du tube, nous remarquons que plus le tube est long et plus l'image est grande et pâle.
Notez que lorsqu'un trou sert d'objectif, comme c'est le cas ici, on l'appelle sténopé.
Fonctionnement du sténopé
Observons le sténopé de la figure 3.

Considérons le point A de l'objet (l'ampoule). Ce point rayonne dans toutes les directions mais seul le pinceau lumineux passant par le sténopé ira éclairer l'écran au point A' (lire "A prime"). Aucun autre pinceau lumineux issu de A n'éclairera ce point puisque la lumière se propage en ligne droite.
Le point A' est l'image du point A.
Nous pouvons étendre ce raisonnement aux points B et C ainsi qu'à tout autre point de l'objet.
En se juxtaposant, les différents points images correspondant à chaque point de l'objet forment l'ensemble de l'image.
Nous pouvons comprendre le renversement de l'image ainsi formée en observant le trajet des rayons lumineux. En effet, nous constatons que plus un point est situé haut sur l'objet et plus son image sera basse sur l'écran, car le seul faisceau lumineux issu de ce point qui atteint l'écran doit passer par le sténopé.
Evidemment, nous pouvons utiliser le même raisonnement pour expliquer l'inversion droite-gauche.
Taille de l'image
De simples considérations géométriques permettent de calculer la taille de l'image.
En examinant la figure 3, nous voyons que le triangle ABO est semblable au triangle A'B'O', nous en déduisons que :

Autrement dit, la taille de l'image est proportionnelle à la distance sténopé-écran et inversement proportionnelle à la distance sténopé-objet (si vous ne comprenez pas cette formule mathématique, je vous invite à lire "Notions de mathématiques").
Exemple : si la distance entre l'écran et le sténopé vaut le quart de la distance du sténopé à l'objet, alors l'image sera quatre fois plus petite que l'ampoule.
Netteté de l'image
L'image sera d'autant plus nette que le trou sera étroit car les pinceaux que nous considérions plus haut seront plus fins.
Luminosité de l'image
Si nous doublons les dimensions de l'image en doublant la distance sténopé-écran le flux lumineux va s'étaler sur une image deux fois plus large et deux fois plus haute donc sur une surface quatre fois plus grande. En conséquence, l'image sera quatre fois moins lumineuse.
La luminosité de l'image est inversement proportionnelle au carré de la distance sténopé-écran.
Applications
Malgré sa simplicité et ses limites ce procédé a été employé pour réaliser les premiers appareils photographiques. Le montage était similaire mais on utilisait une plaque photographique à la place de l'écran en papier transparent.
La faible luminosité de l'image et le manque de sensibilité des émulsions photographiques de l'époque conduisaient couramment à des temps de pose de plusieurs dizaines de minutes, pour des scènes situées en plein soleil.
Améliorations du procédé
Perçons un deuxième sténopé de même diamètre et dans le même carton que le premier. Nous voyons alors deux images distinctes sur l'écran. Ces deux images sont identiques et de même luminosité.
Il serait très intéressant de dévier les pinceaux lumineux issus de l'un des sténopés pour que l'image qu'il forme se superpose à l'autre image. Ainsi nous aurions une image résultante deux fois plus lumineuse sans que la netteté en souffre.
En suivant cette idée, nous pourrions ensuite percer dans le carton des milliers de sténopés. En déviant la lumière issue de chacun d'eux de façon à ce que toutes les images se superposent, nous obtiendrions une image résultante lumineuse et aussi nette que la première. Il nous faut donc étudier des moyens pour dévier la lumière, c'est ce que nous allons faire dans la suite de cet article.
Conclusion
En étudiant le sténopé nous avons appris à diviser l'ensemble de la lumière émise par un objet en une multitude de pinceaux lumineux, et nous les avons considérés séparément dans leur cheminement à travers le montage. Vous rencontrerez souvent ce type de démarche dans les livres d'optique.
Expérience
Comme nous le disions plus haut, la lumière se propage en ligne droite. En fait, ceci est vrai lorsqu'elle se propage dans un milieu isotrope, c'est à dire dans un milieu dont les propriétés physiques sont les mêmes dans toutes les directions. Le vide interstellaire est un milieu isotrope, et en première approximation l'air en est un.
Des faits d'observation quotidienne nous montrent que la lumière peut être déviée : un bâton semble se tordre lorsque nous plongeons une de ses extrémités dans l'eau, des mirages nous montrent de l'eau en plein désert, des mauvaises vitres semblent déformer les scènes vues à travers, etc.
Imaginons un rayon lumineux se propageant dans l'air qui pénètre dans un bloc de verre avec un angle d'incidence i (figure 4).

La surface de séparation des deux milieux se nomme dioptre. N est la normale au dioptre, c'est à dire la ligne imaginaire perpendiculaire au dioptre et passant par M qui est le point d'intersection entre le rayon de lumière et le dioptre.
Le rayon lumineux est dévié au passage du dioptre, il fait un angle r avec la normale N qui est plus petit que l'angle i. On dit que le faisceau est réfracté au passage du dioptre.
On observe que le rayon incident, le rayon réfracté et la normale à la surface de séparation sont dans un même plan.
Imaginons maintenant dans ce plan un cercle centré sur le point M, il intercepte le rayon lumineux en A et en B (figure 5).
Traçons deux segments de droites perpendiculaires à la normale et passant par A et B, ils coupent la normale respectivement en X et en Y.
Une étude quantitative de la réfraction nous montre que le rapport entre les longueurs de AX et YB est constant quel que soit l'angle d'incidence i. On appelle ce rapport l'indice de réfraction du verre, il est environ égal à 1,5.
Une étude plus approfondie de ce phénomène nous donne le résultat suivant :
Cette relation est la loi de Descartes (René Descartes 1596 - 1650), du moins c'est ainsi qu'on la nomme souvent en France. Les anglo-saxons l'appellent plutôt loi de Snell (Willebrord Snel Van Royen, dit Willebrordus Snellius était un astronome et mathématicien hollandais 1580 - 1626). Pour mettre tout le monde d'accord, on dit aussi loi de Snell-Descartes.
Cette propriété a été décrite expérimentalement par Snellius et interprété théoriquement par Descartes.
Nous avons considéré jusqu'ici que le faisceau part du point A dans l'air et arrive au point B dans le verre après avoir traversé le dioptre au point M. Si nous considérons un faisceau lumineux partant de B et allant vers M il sera réfracté de façon à passer par le point A. Le parcours du faisceau ne dépend donc pas du sens de propagation.
Si la lumière s'était propagée en ligne droite pour se rendre de A à B, la durée de son parcours aurait été plus longue. En effet l'épaisseur de verre traversée aurait été plus grande, et la vitesse de la lumière dans ce corps est plus petite que dans l'air. En poussant plus loin notre raisonnement nous remarquerions que la lumière prend, en passant par M le chemin le plus court en temps pour aller de A en B.
La lumière prend toujours le chemin le plus rapide pour se propager d'un point à un autre (dans un milieu isotrope ce chemin est la ligne droite).
Réfraction et déviation des faisceaux lumineux
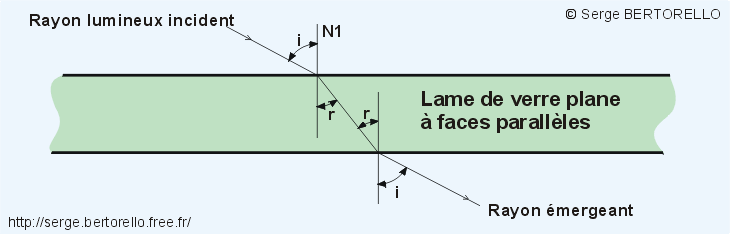
Si nous dirigeons notre faisceau lumineux sur une lame de verre plane à faces parallèles, il sera dévié une première fois par le dioptre air-verre et une seconde fois, en sens inverse par le dioptre verre-air (figure 6).
Le faisceau émergent de la lame se propage selon une direction parallèle au faisceau incident, il n'est donc pas dévié.
Considérons maintenant une pièce de verre dont les faces sont planes mais pas parallèles. En optique un tel objet est couramment appelé prisme.
Cette fois le faisceau sera dévié par le prisme d'un angle d'autant plus important que l'angle au sommet du prisme sera grand.
Nous savons donc maintenant comment dévier les rayons lumineux.
Les lentilles convergentes
Reprenons notre idée du double sténopé, nous avons vu qu'il nous fournit deux images décalées. Avec un prisme adéquat nous pouvons faire superposer les deux images (figure 8).
Si notre montage est bien conçu, nous obtenons une image deux fois plus lumineuse et aussi nette qu'avec un seul sténopé. Si nous perçons d'autres sténopés et que nous équipons chacun d'eux d'un prisme convenable, nous gagnerons encore en luminosité sans nuire à la netteté.
Si nous continuons encore à rajouter des sténopés, ceux-ci vont fusionner en un seul trou de grand diamètre et les prismes vont fusionner en une seule pièce de verre à faces sphériques. Nous venons d'inventer une lentille convergente (figure 9).
Comme nous en avons l'habitude, analysons le parcours des rayons lumineux.
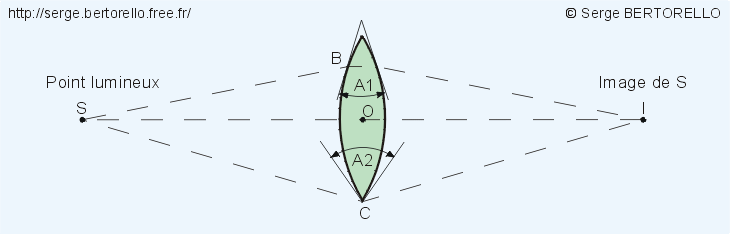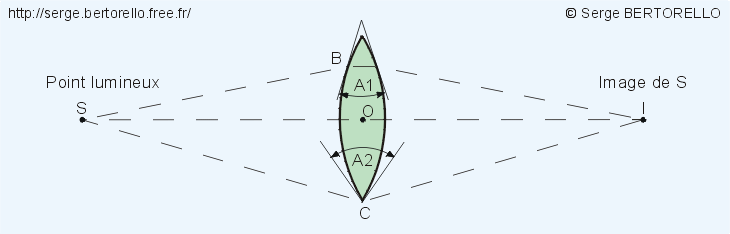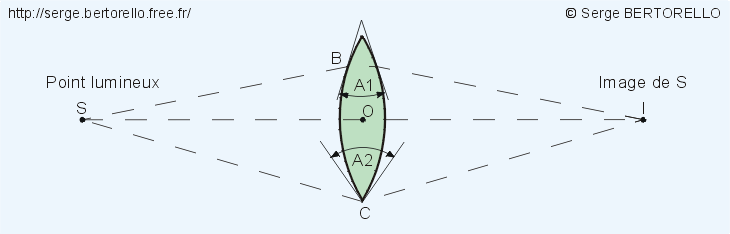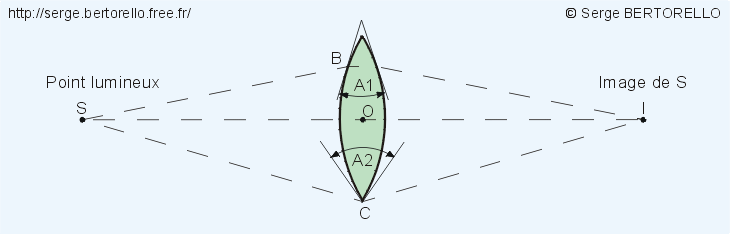
Le faisceau lumineux issu de S et passant par O, centre de la lentille, ne sera pas dévié car en ce point les faces sont parallèles.
Le faisceau passant par B sera dévié car en ce point les deux faces font un angle A1 non nul.
Le pinceau passant par C sera encore plus dévié que le précédent car en C les deux faces font un angle A2 supérieur à A1.
Les faisceaux lumineux issus de S et tombant sur la lentille seront d'autant plus déviés qu'ils seront éloignés de l'axe, et si le point S n'est pas trop proche de la lentille, les faisceaux émergents iront converger en un point I.
Il convient de faire une remarque. Nous avons montré plus haut, que la lumière emprunte toujours le chemin le plus rapide pour se rendre d'un point à un autre ; il n'est pas obligatoirement unique. Ici la lumière utilise une infinité de chemins différents passant tous à travers la lentille. Tous ces chemins sont parcourus dans le même laps de temps, le temps le plus court que puisse mettre la lumière pour se propager de S à I en passant par la lentille. Cette propriété générale permet de retrouver la plupart des résultats de l'optique géométrique. C'est le "principe de Fermat" du nom du mathématicien français Pierre FERMAT (1601 - 1665).
Considérons maintenant un deuxième point lumineux S' situé à la même distance que S (figure 10).
Les rayons lumineux émis par S' vont converger en I' situé à la même distance que I.
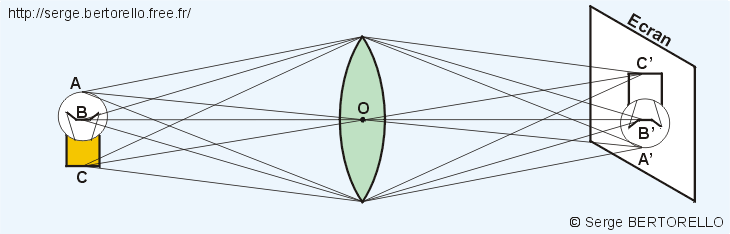
Voyons le cas où nous avons un ensemble de points lumineux en reprenant notre ampoule électrique à filament et à verre clair (figure 11).
Mettons un écran de papier au lieu où convergent les pinceaux lumineux. Nous voyons alors sur cet écran une image beaucoup plus lumineuse et nette qu'avec l'utilisation du sténopé.
Le mécanisme de formation de l'image est très semblable au cas du sténopé mais nous utilisons cette fois une plus grande quantité de la lumière issue de l'objet. Notez aussi que l'image n'est nette que pour une seule position de l'écran.
Distance focale d'une lentille convergente
Dans le montage précédent, si nous éloignons la lampe de la lentille, la position de l'image nette va se rapprocher de cette dernière jusqu'à une distance limite qui est caractéristique de la lentille étudiée. Cette distance est nommée distance focale.
Dirigeons l'axe de notre lentille vers une étoile, c'est à dire vers un objet lumineux que nous pouvons considérer, avec une très bonne approximation, ponctuel et situé infiniment loin (figure 12).
Puisque cette étoile est située à l'infini, les rayons qui nous en arrivent sont parallèles entre eux. Après la traversée de la lentille ils vont converger au point F nommé "foyer de la lentille". La distance OF est la distance focale de la lentille.
Le plan perpendiculaire à l'axe de la lentille et passant par le foyer s'appelle le plan focal. C'est sur ce plan que se forme l'image nette de tout objet situé à l'infini devant la lentille convergente.
Une lunette
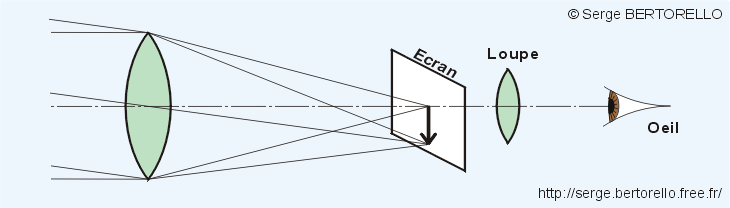
Dirigeons notre lentille vers un objet éloigné, plaçons un écran en papier calque au foyer. En plaçant notre il derrière l'écran nous voyons l'image renversée de cet objet. Si nous observons cette image avec une loupe nous verrons l'objet plus grand qu'à l'il nu (figure 13).
Otons maintenant le papier calque, nous voyons toujours l'image.
Ces deux lentilles constituent une lunette astronomique simplifiée, nous l'étudierons plus loin.
Les lentilles divergentes
Les lentilles que nous venons d'étudier sont plus épaisses au centre, nous allons constater des propriétés différentes pour des lentilles dont les bords sont plus épais que le centre, ce sont des lentilles divergentes.
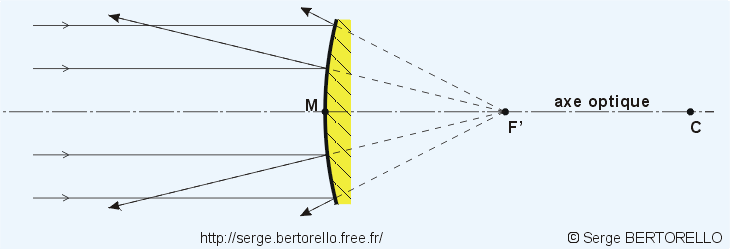
La figure 14 montre la transformation subie par un faisceau de rayons lumineux parallèles, lorsqu'il traverse une lentille divergente. Cela correspond à l'observation à travers cette lentille d'un point lumineux très éloigné (exemple : une étoile).
Les rayons sortent de la lentille selon des directions qui divergent du point F', que l'on nomme foyer virtuel de la lentille. Elle ne forme pas d'image d'un objet à l'infini, mais un il placé derrière elle (à droite sur la figure 14) verrait cet objet comme s'il se situait en F'.
OF' est la distance focale de la lentille, ici elle est exprimée par un nombre négatif.
La cambrure
Jusqu'à présent nous avons considéré qu'une lentille n'est définie que par sa distance focale. En fait, il faut aussi tenir compte de la cambrure, il s'agit d'un nombre qui caractérise la forme de la lentille et qui est numériquement égal à la moyenne des courbures des deux faces de la lentille.
La figure 15 montre des profils de lentilles de même distance focale mais de cambrures différentes.
La cambrure des lentilles n'intervient pas dans le principe de formation des images, mais elle influe sur la qualité de celles-ci.
Numériquement, la cambrure γ d'une lentille mince est égale à la moyenne des courbures de ses faces :
r1 et r2 désignent les rayons de courbure des faces de la lentille considérée. La cambrure s'exprime en dioptries quand les rayons de courbure sont mesurés en mètres.
Expérience
Il existe une autre méthode pour dévier la lumière, c'est la réflexion. Ce phénomène est mieux connu du grand public, rappelons-en les lois qui le régissent.
Un faisceau lumineux tombant sur un miroir se réfléchit selon une direction, par rapport à la normale, symétrique à la direction du faisceau incident (figure 16).
L'angle d'incidence est égal à l'angle de réflexion : i = r
Cette loi ne dépend pas des caractéristiques du milieu transparent dans lequel se propage la lumière avant et après la réflexion. Ceci signifie que l'angle de réflexion du rayon lumineux sera le même si on place le miroir dans l'eau (par exemple).
Images et miroirs
Plaçons un miroir derrière un sténopé et projetons grâce à cet ensemble l'image d'une bougie sur un écran (figure 17).
En utilisant la loi de la réflexion énoncée plus haut, nous pouvons comprendre le mécanisme de formation de cette image.
En fait, la figure 17 ressemble beaucoup à la figure 3 que l'on aurait repliée sur elle-même au niveau du sténopé. Le principe de formation de l'image est identique.
Nous pouvons remplacer l'ensemble sténopé-miroir par un très petit miroir, de même taille que le sténopé, et nous ne changerons rien au résultat du montage.
En utilisant d'autres petits miroirs judicieusement placés pour faire superposer chacune de leurs images, nous pouvons augmenter la luminosité de l'image finale (figure 18).
De même que, plus haut, nous avons fait fusionner plusieurs prismes en une seule lentille, nous pouvons remplacer ces petits miroirs par un seul qui aura la forme adéquate pour que l'image soit nette. En première approximation nous dirons que cette forme est une sphère.
Ce miroir sphérique est concave et convergent.
Considérons maintenant un point lumineux situé au centre de courbure d'un miroir sphérique, c'est à dire au centre de la sphère dont la surface du miroir est une portion (figure 19).
Tout rayon lumineux issu de S et atteignant le miroir revient en S en suivant le même chemin, car il rencontre toujours une surface qui lui est perpendiculaire. Autrement dit l'image de S se forme sur S lui-même.
Voyons ce qu'il se passe si nous décalons notre point lumineux (figure 20).
Nous constatons que l'image se décale d'une même quantité, mais en sens opposé.
Revenons maintenant à notre bougie et plaçons-la au voisinage du centre de courbure C du miroir.
Nous obtenons une image nette et inversée sur le plan de la bougie.
Si nous éloignons notre bougie du miroir, la position de l'image nette va se déplacer vers le miroir.
Distance focale d'un miroir concave
Lorsque l'objet sera très éloigné l'image se formera au foyer du miroir, elle sera évidemment beaucoup plus petite (figure 22).
La géométrie nous enseigne que le foyer d'un miroir est à mi-chemin entre sa surface et son centre de courbure. Autrement dit la distance focale MF vaut la moitié du rayon de courbure MC.
Remarque : Nous avons dit que l'image obtenue est simplement renversée, en fait ceci est vrai lorsque nous l'examinons depuis le miroir. Si, comme nous l'avons fait avec les lentilles, nous prenons une feuille de papier calque en guise d'écran et si nous observons l'image par transparence, alors cette image sera symétrique par rapport à l'objet. C'est à dire que l'image d'une main droite ressemblera à une main gauche.
Un télescope est un instrument similaire à la lunette astronomique mais l'objectif est un miroir ; nous dirons que c'est un réflecteur.
Si nous voulons observer l'image fournie par un miroir, nous devons nous placer entre le miroir et l'objet, ceci risque de compromettre la qualité de notre observation. Par conséquent nous allons utiliser un petit miroir plan pour renvoyer cette image sur le côté (figure 23).
Ceci est le principe du télescope de Newton, car ce grand homme fut le premier à réaliser cet instrument (Sir Isaac NEWTON, 1643 - 1727).
Remarque : Le nom de lunette s'emploie pour des instruments dont l'objectif est réfracteur et celui de télescope pour ceux dont l'objectif est réflecteur.
Les miroirs convexes
Un miroir peut aussi être convexe. La figure 24 nous montre ce qu'il advient à un faisceau de rayons parallèles réfléchi par un miroir sphérique convexe.
Les rayons réfléchis semblent diverger du point F' qui est le foyer virtuel du miroir. Il est à mi-chemin entre le miroir et son centre de courbure C.
Il ne forme pas d'image d'un objet à l'infini, mais un il placé devant lui (à gauche de la figure 24) verrait cet objet comme s'il se situait en F'.
MF' est la distance focale du miroir, elle est exprimée par un nombre négatif. La puissance optique Φ d'une lentille ou d'un miroir est l'inverse de sa distance focale. On l'appelle aussi vergence de la lentille.
La formule suivante donne la puissance d'une lentille mince en fonction de ses rayons de courbure :
Avec :
n = indice de réfraction du verre composant la lentille.
Cette puissance optique s'exprime en dioptries (que l'on note habituellement avec la lettre grecque delta δ). Une puissance de 1δ correspond à une distance focale de 1m. Autrement dit, la puissance optique exprimée en dioptries est l'inverse de la distance focale exprimée en mètres.
Exemple : Considérons une lentille dont la distance focale est 50cm et cherchons sa puissance optique Φ :
Une lentille de 0,5 mètre de distance focale a donc une puissance optique de 2 dioptries.
Les éléments optiques divergents ont une distance focale négative, leur puissance optique est donc négative elle-aussi.
Si on dispose deux lentilles minces l'une contre l'autre (distance négligeable), la puissance optique de ce doublet sera égale à la somme des puissances de ces lentilles.
Exemple : Considérons un doublet constitué d'une lentille convergente de puissance Φ1= 6 δ et d'une lentille divergente de puissance Φ2= -4 δ. La puissance optique résultante du doublet est Φ :
La réflexion vitreuse
Considérons un dioptre qui sépare un milieu d'indice de réfraction n1 et un milieu d'indice n2.
L'intensité de cette réflexion partielle varie en fonction de l'angle d'incidence.
Pour une incidence normale (c'est à dire perpendiculairement au dioptre), chaque face d'une vitre ordinaire dans l'air réfléchit ainsi environ 4% de la lumière (pour plus de détails voir notre Mémento optique).
Considérons maintenant un rayon lumineux qui arrive sur un dioptre air-verre avec une incidence rasante, c'est à dire avec un angle i légèrement inférieur à 90° comme l'illustre la figure 26. Comme nous l'avons appris précédemment, nous constatons l'existence d'un faisceau partiellement réfléchi et le reste du faisceau est réfracté selon un angle r tel que : avec n1 = indice de réfraction de l'air (environ égal à 1) Cette formule nous montre que l'angle de réfraction a une valeur proche de la limite que nous atteindrions avec un angle d'incidence de 90°. Dans ce cas, nous aurions :
Par conséquent, en considérant n1 = 1, nous obtiendrions :
En l'exprimant différemment : Pour un verre optique très commun qui a un indice n2 = 1,52, nous obtenons la valeur limite r = 41°.
Afin d'éviter ces développements mathématiques, nous aurions pu utiliser la construction géométrique de la figure 5 pour trouver cette limite.
La figure 27 illustre que le parcours du faisceau réfracté ne dépend pas du sens de propagation.
Nous considérons ici que la lumière arrive de l'intérieur de la masse de verre avec un angle d'incidence égal à l'angle de réfraction de la figure précédente. On constate que le faisceau partiellement réfléchit se propage maintenant à l'intérieur du verre et le faisceau réfracté suit le même trajet que précédemment mais en sens inverse.
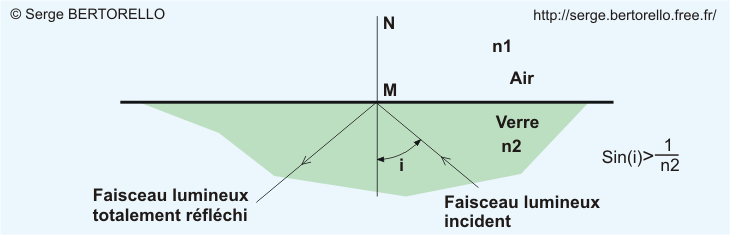
Question : Que devient le faisceau réfracté si l'angle d'incidence a une valeur supérieure à la valeur limite précédemment calculée?
La loi de la réfraction nous indique :
Pour bien comprendre cette façon d'écrire la loi de la réfraction, il faut se rappeler que le rayon vient de l'intérieur de la masse de verre. L'angle i se trouve à présent dans le verre d'indice n2.
Puisque n1=1, nous avons :
Ceci est impossible car le sinus d'un angle ne peut pas être supérieur à 1.
La construction géométrique de la figure 5 aboutit aussi à une impossibilité.
Ceci signifie qu'il n'existe pas de faisceau réfracté dans ce cas de figure. Toute la lumière se retrouve donc concentrée dans le faisceau réfléchi (figure 28), c'est une réflexion totale.
On utilise ce phénomène pour obtenir une réflexion sans déposer de métal sur le verre.
Il s'agit d'un prisme en matériau transparent qui utilise le principe de la réflexion totale sur une ou plusieurs de ses faces. La variété des formes n'est limitée que par l'imagination des opticiens.
Un modèle très courant est un prisme droit en verre dont la base est un triangle isocèle rectangle. Cela signifie qu'il possède un angle droit (90°) et ses deux autres angles sont égaux à 45°. La figure 29 illustre ce prisme en perspective et de profil. Sur les images de droite, elle montre deux dispositions différentes qui utilisent le principe de la réflexion totale. Dans ces configurations, l'angle d'incidence sur le dioptre verre-air a une valeur de 45°. Elle est supérieure à la valeur limite précédemment calculée, c'est pour cela que nous avons une réflexion totale.
Un prisme à réflexion totale est employé comme un miroir plan (ou un ensemble de miroirs plans) avec l'avantage de ne pas nécessiter de métallisation.
On utilise parfois un prisme à réflexion totale comme celui de la figure 29 à la place du miroir plan dans certains télescopes de Newton économiques.
Lors de la conception d'un dispositif autour d'un prisme à réflexion totale, il faut tenir compte de l'épaisseur du verre traversé. Exemple : Pour les deux dispositions de droite sur la figure 29, la traversée du prisme équivaut pour le faisceau lumineux à la traversée d'une lame à faces parallèles. Ceci provoque un décalage du plan focal et une aberration de sphéricité du type "sur-correction" (Voir notre mémento).
Un redresseur permet de redresser une image inversée. Une lunette astronomique donne une image inversée. Pour des usages terrestres, il existe différentes possibilités pour redresser cette image, on peut notamment employer un système de prismes à réflexion totale.
De nombreuses dispositions ont été conçues avec la réflexion totale pour redresser l'image fournie par un objectif. Je vous propose d'examiner sur la figure 30 une solution très répandue, il s'agit du redresseur rencontré dans la plupart des jumelles à prismes et dans certaines longues vues à prismes.
Un petit symbole figurant une demi-flèche permet de suivre l'orientation du faisceau après les réflexions successives afin de comprendre le mécanisme de ce redressement.
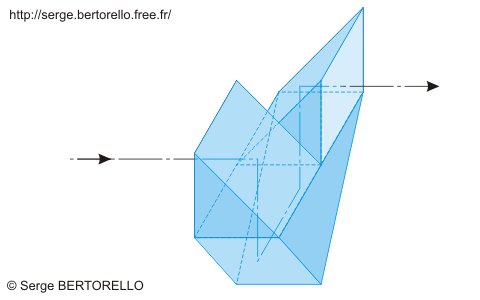
La figure 31 présente une autre composition de redresseur à prismes qui réunit trois prismes à réflexion totale.
On a inventé d'autres types de redresseurs à prismes...
Le lieu où se produit la réflexion avec un dioptre transparent n'est pas une surface d'épaisseur infiniment petite comme on pourrait le supposer en examinant la figure 28. En fait, le phénomène de la réflexion sur un dioptre transparent se produit, après la traversée du dioptre, sur une couche épaisse de quelques longueurs d'ondes de la lumière considérée. Par conséquent, en approchant suffisamment près du dioptre considéré la surface d'un autre objet transparent, on va pouvoir récupérer une partie du flux lumineux.
La figure 32 illustre différents cas obtenus avec un prisme isocèle rectangle comme celui de la figure 29.
Ce dispositif permet d'obtenir une réflexion partielle.
Toutefois en pratique ce phénomène est difficile à maîtriser et on préfère métalliser la face hypoténuse d'un des deux prismes avant de les coller ensemble. L'épaisseur de cette métallisation doit être contrôlée afin d'obtenir une réflexion partielle de 50%. On réalise ainsi un diviseur optique appelé aussi d'une façon imagée "cube séparateur". L'avantage de cette solution est l'égalité des chemins optiques des faisceaux transmis et réfléchi.
Une autre méthode pour obtenir une réflexion partielle consiste à réaliser un miroir semi-transparent. Pour cela, on utilise un miroir en verre sur lequel on dépose une couche de métal réfléchissante. Si l'épaisseur du métal déposé est particulièrement faible (moins de 40 nanomètres), on obtient une surface semi-réfléchissante et donc semi-transparente. Sur une autre page de ce site, je vous propose une étude des techniques du vide et de la métallisation des miroirs.



















Dans les pays anglo-saxons le mot "telescope" désigne indifféremment les réflecteurs ou les réfracteurs, certains ouvrages mal traduits tendent à faire persister une confusion dans ces termes.


r1 et r2 = rayons de courbure des faces de la lentille exprimés en mètres. Le rayon de courbure est positif si le dioptre est convexe vers la lumière incidente, il est négatif si le dioptre a une concavité dirigée vers l'incidence (d'autres auteurs peuvent très bien suivre la considération inverse). Voir aussi le mémento optique.

Φ = Φ1 + Φ2 = 6 - 4 = 2 δ
Un faisceau incident sur ce dioptre sera partiellement réfléchi.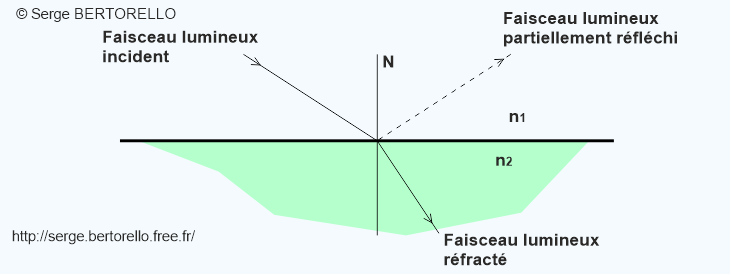

n1.sin i = n2.sin r
n2 = indice de réfraction du verre
sin i = sin 90° = 1
n2.sin r = 1


Prenons par exemple : i = 45°
n2.sin i = n1.sin r
sin r = n2.sin i = 1,52 sin 45° = 1,52 x 0,707 = 1,075

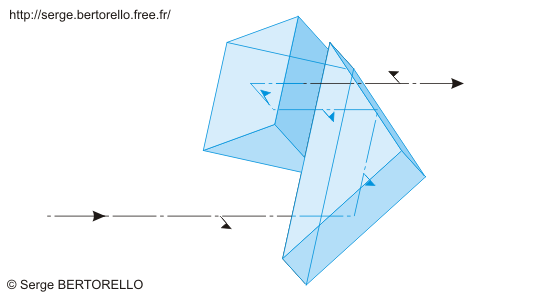
(Paolo Ignazio Pietro Porro, opticien italien 1801-1875).

A gauche : Le prisme est isolé, la réflexion est totale.
Au centre : Un deuxième prisme est rapproché de la face réfléchissante à quelques longueurs d'ondes, transmission et réflexion se partagent le faisceau incident.
En rapprochant les prismes, on augmente la transmission.
En éloignant les prismes, on augmente la réflexion.
A droite : Les prismes sont en contact, tout le faisceau est transmis.

