NOTIONS D'OPTIQUE

Le télescope de Gregory

La première description d'un télescope (à réflexion) que l'histoire a retenue est celle que le mathématicien écossais James Gregory (novembre 1638 - octobre 1675) a publiée en 1663. Il n'a jamais construit l'instrument dont il est l'inventeur car il n'a pas réussi à se procurer des miroirs de qualité suffisante. C'est Robert Hooke (1635 - 1703) qui fabriqua plus tard le premier télescope de Gregory.

Le télescope de Gregory a donc été conçu avant le télescope de Newton mais son premier exemplaire a été construit après.

Il est intéressant de noter que diverses combinaisons de miroirs destinées à constituer des télescopes avaient été décrites bien avant la fabrication des télescopes de Newton et de Gregory. Mais ces instruments n'ont jamais été fabriqués car cela aurait été très difficile et parce que ces solutions n'ont pas eu d'intérêt pratique.

Figure 21 : Vue en coupe d'un télescope de Gregory.
Cliquer sur l'image pour obtenir les caractéristiques détaillées d'un télescope de Gregory.

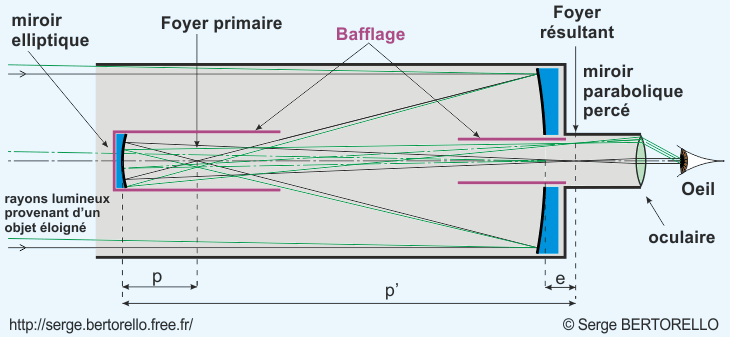
Analysons le fonctionnement du télescope de Gregory. Il utilise deux miroirs convergents. Le miroir primaire est parabolique (coefficient de déformation b₁ = -1) et il forme une image en son foyer (foyer primaire). Celle-ci est récupérée par le miroir secondaire concave et elliptique qui la projette en l'agrandissant vers le centre du miroir primaire (foyer résultant). Cette dernière image est analysée avec un oculaire par l'observateur qui est placé derrière le miroir principal.

Il faut donc que le miroir primaire soit percé en son centre pour laisser passer le faisceau de lumière.

Les formules suivantes caractérisent le télescope de Gregory, toutes les longueurs doivent être exprimées avec un signe positif. Nous considérons aussi que le foyer se situe après la surface réfléchissante du miroir principal à la distance de dégagement "e".

Calculons la position du miroir secondaire :

       [23]

est le rayon de courbure du miroir secondaire :

     [24]

D₂ est le diamètre du miroir secondaire, D₁ est le diamètre du miroir primaire. La formule suivante nous indique la valeur minimale de D₂. En fait, il faut lui donner une valeur légèrement supérieure pour avoir un champ de pleine lumière non nul :

           [25]

Le miroir secondaire du Gregory a une méridienne elliptique, son coefficient de déformation b₂ est donc plus faible que celui d'une parabole (en valeur absolue) :

       [26]

On remarque que : -1 < b₂ < 0      

Le miroir primaire fournit une image renversée et elle est renversée à nouveau par le secondaire. Résultat : le télescope de Gregory donne une image redressée. Cette caractéristique l'a rendu très populaire pendant les 18^ième et 19^ième siècles durant lesquels il était couramment utilisé comme longue-vue. Il était particulièrement apprécié pour les usages terrestres.

Sur la figure 21, nous pouvons constater que la lumière parasite peut arriver directement sur l'oculaire en dégradant ainsi le contraste de l'image observée. Pour éviter cette lumière parasite, on dispose un bafflage constitué par deux tubes opaques. Un d'eux est disposé autour du miroir secondaire et prolongé en direction du primaire. Le second est placé dans le trou du primaire et prolongé vers le secondaire. S'il est conçu correctement, ce bafflage du télescope de Gregory est très efficace.

L'image fournie par le miroir primaire est renversée et agrandie dans le rapport p'/p. La distance focale est allongée dans les mêmes proportions.

Considérons par exemple un télescope de Gregory dont le miroir primaire est ouvert à F/D=3 et dont le miroir secondaire agrandit 5x l'image. Cet instrument a donc un rapport d'ouverture résultant F/D=15 mais il aura approximativement le même encombrement qu'un télescope de Newton de même diamètre et ouvert seulement à F/D=5. La combinaison de Gregory permet donc d'obtenir une grande distance focale sous un encombrement réduit.

Notons toutefois que l'encombrement de la combinaison de Gregory est plus important quand le grandissement du secondaire est faible et dans ce cas le diamètre du petit miroir peut devenir prohibitif.

Aujourd'hui la combinaison inventée par James Gregory est délaissée malgré ses bonnes qualités optiques. Pourtant, la fabrication de cet instrument doit être relativement aisée, notamment par un amateur, puisque la réalisation de son miroir secondaire semble plus facile que celle d'un bon miroir plan pour un télescope de Newton.

Attention : Un actuel constructeur de télescopes se nomme Gregory et cela peut provoquer un malentendu car pour certaines personnes, un télescope de Gregory est tout simplement un télescope de la marque Gregory.