NOTIONS D'OPTIQUE
POUR LES ASTRONOMES AMATEURS
La vitesse de propagation de la lumière
- "La lumière en se répandant emploie du temps"
Christiaan HUYGENS (1629 - 1695).
L'étude de la vitesse de propagation de la lumière est intimement liée à l'étude de sa nature.
La lumière est nécessaire à la vue
A propos de la lumière, l'homme a fait depuis longtemps les constatations de base comme par exemple : "Il faut de la lumière pour voir". Cette remarque semble extraite des poésies commémoratives des exploits de Jacques LA PALICE (1470-1525), pourtant elle a des conséquences intéressantes. Elle nous aide à comprendre (entre autres choses) qu'un objet doit être éclairé pour être vu s'il n'est pas lumineux par lui-même. Car contrairement au sens du toucher qui n'a pas besoin d'un intermédiaire, la vue a besoin de la lumière.
La vue est le sens le plus riche en informations sur notre environnement. Sans la vue ou sans la lumière, nous sommes grandement handicapés, notre conscience du monde extérieur est altérée. La figure suivante nous démontre cet aspect avec humour.

L'avance progressive de la lumière
Depuis longtemps, une question a hanté l'esprit des physiciens : "A quelle vitesse se déplace ce rayonnement ?"
Pour certains, sa propagation devait être instantanée. Pour d'autres, ce signal présentait des analogies avec le son. Or ce dernier se déplace à une vitesse finie, c'est évident quand on regarde de loin le tir d'une arme à feu. On voit nettement le coup de feu avant de l'entendre. Cette analogie amenait à penser que la lumière se déplace progressivement elle aussi.
Ces deux idées se sont affrontées pendant longtemps. Des expérimentateurs ont même essayé de mesurer la célérité de la lumière. On cite parfois Galilée qui tentait en vain cette mesure pendant la nuit en échangeant des signaux lumineux avec un partenaire qui se trouvait de l'autre côté d'une vallée. La lumière va trop vite pour cette méthode.
Galileo Galilei dit Galilée que certains considèrent comme l'initiateur de la science expérimentale est né à Pise le 15 février 1564 et mort à Arcetri près de Florence le 8 janvier 1642.
En 1676 à l'observatoire de Paris, Olaüs RÖMER (1644-1710) étudiait le mouvement des satellites de la planète Jupiter. Il a constaté une avance ou un retard de quelques minutes de ces astres sur les prévisions. Une analyse approfondie lui montra une relation entre cette anomalie et la position relative de la Terre par rapport à Jupiter. Il déduisit alors que ces défauts de ponctualité sont dus à la vitesse de la lumière. Quand la Terre est au plus près de Jupiter, il voyait les satellites en avance sur les éphémérides car la distance parcourue par la lumière est plus petite. Inversement, il notait un retard quand les mouvements orbitaux éloignent les deux planètes.
Grâce à ses observations, Olaüs RÖMER a déterminé une estimation fort honorable de la vitesse de la lumière dans le vide. La valeur trouvée varie selon les auteurs qui la rapportent mais elle avait le bon ordre de grandeur.
En 1849, Hippolyte FIZEAU (1819-1896) a imaginé une méthode "terrestre" pour mesurer la vitesse de la lumière. Il utilisait une roue dentée qui occultait périodiquement un faisceau auquel il faisait parcourir une grande distance. Cette technique permit d'améliorer la connaissance de la vitesse de la lumière. Toutefois, la grande distance parcourue par le faisceau lumineux ne permettait pas d'analyser la propagation de la lumière dans un autre milieu que l'air.
Les anciens avaient compris que la lumière est rayonnée par certains corps et réfléchie par d'autres. Les idées se sont succédé pour expliquer la nature de ce rayonnement.
Au début du 19ième siècle, les physiciens étaient partagés en deux groupes qui défendaient des théories opposées. Il y avait ceux qui affirmaient que la lumière est une vibration ou une onde et ceux qui considéraient que le rayonnement lumineux est un flot de particules microscopiques émises par les corps incandescents.
Une étude théorique approfondie concluait que la vitesse de la lumière devait être plus grande (que dans le vide) lors de la propagation dans des corps transparents (réfringents) si elle était constituée de corpuscules. Par contre, on montrait qu'elle devait être plus lente dans ce cas si elle était de nature ondulatoire. La mesure de la célérité de la lumière dans un matériau transparent devait donc permettre de sélectionner la meilleure théorie.
Léon FOUCAULT (1819-1868) a été un physicien très talentueux auquel nous devons de nombreuses techniques qui ont fait avancer la science à grands pas. Notamment, j'aime bien rappeler que grâce à lui, la ville de Marseille peut s'enorgueillir de posséder le premier grand télescope à miroir en verre, il en était l'inventeur.
En 1850, Léon FOUCAULT a mis au point une méthode avec laquelle il a mesuré la vitesse de la lumière dans l'eau. Dans ce milieu, elle se propage moins vite que dans le vide. Les physiciens ont alors conclu à une nature ondulatoire de la lumière.

Si le miroir tourne à 1000 tours/s, l=15m et d=10m alors le rayon revient à 12,5mm de la source quand la distance l est parcourue dans l'air.
Dans ce montage, un miroir plan tourne sur lui-même avec une grande vitesse. Son axe de rotation M est situé au centre de courbure d'un miroir sphérique. Un fin rayon de lumière est émis par la source S vers le miroir plan. Périodiquement, ce dernier réfléchit le rayon en direction du miroir sphérique. A ce moment, le rayon est renvoyé vers le petit miroir mais entre-temps celui-ci a légèrement pivoté d'un angle α et il renvoie donc le rayon à côté de la source (il fait un angle 2α avec le rayon incident).
L'écartement entre la source S et l'image retournée par le montage est inversement proportionnel à la vitesse de la lumière. Cette méthode est élégante car elle est simple à mettre en œuvre et elle se contente d'une faible distance de parcours de la lumière (quelques mètres). Elle peut donc être utilisée pour analyser le comportement de la lumière dans un milieu quelconque.
A partir de l'expérience de FOUCAULT, la communauté scientifique était convaincue de la nature ondulatoire de la lumière. La lumière est donc une oscillation, une "vibration". Pour que les physiciens admettent cela, il fallait définir la nature du corps ou du milieu qui transporte cette vibration. Comme le son est une vibration de l'air, il fallait que la lumière soit une vibration d'un support qui restait à découvrir. Pour répondre à cela, on a conçu théoriquement un fluide qui envahit tout l'univers même le vide, on l'a nommé l'éther. Les physiciens considéraient donc que la lumière est une vibration de l'éther.
Cette attitude des physiciens était imposée par la mécanique. Cette discipline de la physique avait déjà eu de nombreux succès et elle semblait pouvoir expliquer tous les secrets de la matière et, pourquoi pas, de la lumière.
L'hypothèse de l'éther explique certains aspects du comportement de la lumière qui sont analogues aux propriétés du son. Elle permet notamment de comprendre pourquoi la vitesse de la lumière est indépendante de la vitesse de sa source.
La vitesse de la lumière ne dépend pas de la vitesse de la source
Un fait d'observation très banal en astronomie démontre de façon évidente que la vitesse de la lumière ne dépend pas de la vitesse de sa source. Il s'agit du mouvement apparent des étoiles doubles. La figure suivante nous montre un exemple de couple d'étoiles en mouvement.

Le comportement des étoiles doubles (ou multiples) s'apparente aux mouvements des planètes autour du Soleil. Leur observation a permis de vérifier qu'elles obéissent aux mêmes lois que les planètes, elles sont soumises aux lois de KEPLER (Johannes KEPLER 1571-1630). Les scientifiques ont rapidement exhibé ce fait pour affirmer que la loi de la gravitation découverte par NEWTON (Sir Isaac NEWTON, 1642 - 1727) pour expliquer les lois de KEPLER est universelle car elle s'applique aussi sur les systèmes stellaires les plus éloignés.
La figure suivante montre la propagation de la lumière en deux points diamétralement opposés de l'orbite d'un couple d'étoiles. Dans le cas de cette figure, nous considérons que la vitesse de la lumière ne dépend pas du rapprochement ou de l'éloignement de l'étoile observée.

Dans ce cas, l'observateur reçoit les rayons lumineux dans l'ordre chronologique suivant lequel ils ont été émis. Il observe donc un spectacle comparable à la figure 3.
Voyons ce qu'il se passerait si la vitesse de la lumière s'ajoutait à la vitesse de l'étoile.

Comme le suggère cette dernière animation, nous pourrions voir simultanément la plus petite étoile en deux points opposés de son orbite ! En effet, dans le cas représenté, la vitesse de la lumière se composerait avec celle de l'étoile observée. Elle s'ajouterait à la vitesse de l'étoile. Quand l'astre s'éloigne la lumière nous parviendrait plus lentement. Par contre elle nous arriverait plus vite quand l'étoile se rapproche. Dans certains cas, la lumière de l'étoile qui se rapproche rattraperait celle qu'elle aurait émise en s'éloignant.
Ceci serait un cas particulier qui serait tout à fait vraisemblable. En tous cas, l'étude du mouvement des étoiles doubles serait fort compliquée car il faudrait une analyse mathématique sophistiquée des observations pour comprendre le comportement réel des étoiles doubles. Le respect des lois de KEPLER par les étoiles doubles n'aurait pas été aussi évident.
En conclusion, nous pouvons affirmer que la vitesse de propagation la lumière n'est pas influencée par le mouvement de l'étoile qui la rayonne.
Ainsi, n'importe quel astronome amateur méfiant peut vérifier que la vitesse de la lumière ne dépend pas de la vitesse de la source qui l'a émise. Il lui suffit d'observer les étoiles doubles.
N'oublions pas notre constatation :
La vitesse de la lumière ne dépend pas de la vitesse de la source qui l'a émise.
Il se produit un phénomène semblable pour le son. La vitesse du son que nous percevons d'un objet en mouvement (une moto par exemple) ne dépend pas de la vitesse de cet objet. Elle dépend par contre de notre propre vitesse par rapport à l'air (ne pas confondre avec l'effet DOPPLER-FIZEAU). Par analogie, les physiciens ont pensé que la vitesse de propagation de la lumière doit être influencée par la vitesse avec laquelle nous nous déplaçons dans l'éther.
L'expérience de MICHELSON-MORLEY
Après la démonstration de Léon FOUCAULT en 1850, l'existence de l'éther était admise par la communauté scientifique. Même le physicien James Clerk MAXWELL (1831-1879), dont les travaux sur l'électromagnétisme font toujours référence, était persuadé de son existence. Cependant, aucune expérience n'avait pu le mettre en évidence.
Puisque la terre se déplace à 30 kilomètres par seconde dans son mouvement de révolution autour du Soleil, on a envisagé de démontrer l'existence de l'éther en analysant la vitesse de propagation de la lumière.

Si la Terre se déplace dans l'éther et si la lumière se propage avec une vitesse constante dans l'éther, on doit constater une valeur différente de la vitesse de la lumière selon la direction dans laquelle on l'étudie. Une mesure faite dans le sens d'avancement de la Terre donnera une valeur plus petite que lorsqu'elle est effectuée dans la direction perpendiculaire.
La difficulté est que la Terre se déplace à 30 kilomètres par seconde sur son orbite (environ), c'est à dire 10 000 fois moins vite que la lumière. Il faut donc une méthode très sensible pour mettre en évidence la petite différence de vitesse de la lumière provoquée par le déplacement de notre planète.
Vers la fin du 19ième siècle, diverses expériences avaient montré que la vitesse de la lumière n'était pas autant influencée par le mouvement de la terre qu'on le prévoyait. Toutefois, leur manque de sensibilité ne permettait pas de conclure nettement. On a alors échafaudé des théories compliquées pour affirmer que l'éther est plus ou moins entraîné par la Terre dans son mouvement. Cela signifiait que la variation de la vitesse de la lumière devait être plus petite que prévue. Il fallait donc une méthode très sensible pour analyser ce "vent d'éther".
Il faut quand même noter que certaines observations contredisaient déjà l'idée de l'entraînement de l'éther. Ainsi, l'aberration de la lumière est connue depuis 1728 grâce à James BRADLEY (1693-1762). Elle provoque un léger déplacement de la position des étoiles en fonction de la composition des vitesses de la Terre et de la lumière. Un entraînement de l'éther est incompatible avec cette interprétation.
En 1886, Albert Abraham MICHELSON (1852-1931) et Edward Williams MORLEY (1838-1923) réalisèrent une expérience célèbre dans laquelle ils comparaient le temps mis par la lumière pour effectuer deux parcours perpendiculaires de même longueur. C'est l'interféromètre de MICHELSON qui a eu de très nombreuses applications depuis.

Le faisceau lumineux qui est émis par la source S est partagé en deux rayons perpendiculaires par un miroir semi-réfléchissant. L'un d'eux est visualisé en bleu et l'autre en orange (Ces couleurs sont utilisées pour la clarté de l'illustration. Notez bien qu'il n'y a aucune intervention des couleurs dans l'expérience). Chacun de ceux-ci va ensuite se réfléchir sur un miroir qui le renvoie vers le point où ils se sont séparés. A partir de là, ils vont suivre la même direction, ils vont interférer et ils vont être reçus par un œil (ou un récepteur) figuré en bas de l'image. En conséquence, l'œil (ou le récepteur) qui les reçoit percevra une intensité lumineuse qui dépend de la phase respective des deux signaux.
Ainsi ce dispositif permet de mettre en évidence un infime retard d'un faisceau sur l'autre. L'idée des expérimentateurs consistait à orienter un des faisceaux dans le sens de déplacement de la Terre autour du Soleil. Selon la théorie de l'éther il aurait pris un retard sensible sur l'autre rayon car ce dernier aurait suivi un parcours perpendiculaire au "vent d'éther" et sa vitesse n'aurait pas été influencée.
Avec la théorie de l'éther, le faisceau orienté dans la même direction que le mouvement de la Terre devrait être retardé dans son aller-retour. Le retard subit en se propageant dans le même sens que notre planète ne serait que partiellement compensé par l'avance obtenue avec le parcours dans l'autre sens.
Imaginons un nageur qui va remonter une rivière sur 1 km à la vitesse de 2 km/h par rapport à l'eau (en nageant) avec une eau qui s'écoule à 1 km/h. Donc arrivé à une distance de 1 km, il fait demi-tour et retourne à son point de départ avec la même vitesse relative.
Il a donc parcouru 2 km à la vitesse (relative) de 2 km/h.
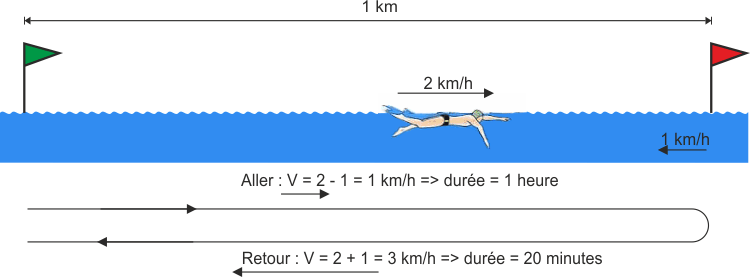
A l'aller en luttant contre le courant, il avait une vitesse de 2 - 1 = 1 Km/h par rapport à la rive. Cette partie a nécessité 1 heure.
Au retour poussé par le courant, sa vitesse était de 2 + 1 = 3 km/h par rapport à la rive. Le retour a duré 1/3 heure = 20 minutes.
Conclusion : avec sa vitesse de nage de 2 km/h, il aurait dû parcourir les 2 km en 1 heure mais il a effectué ce trajet en 1h 20mn. Le courant l'a donc bien ralenti. Son accélération dans un sens n'a pas compensé totalement son ralentissement dans l'autre sens.
C'est analogue à ce qui se produirait si la Terre se déplaçait dans l'éther. La durée d'un aller-retour d'un faisceau lumineux dans le sens d'avancement de la Terre serait accrue par rapport à une direction perpendiculaire.
Pour rapporter notre analogie au cas qui nous intéresse ici, il suffit d'échanger la vitesse du nageur avec celle de la lumière et la vitesse de l'eau par rapport à la rive avec la vitesse de la Terre dans l'éther.
La figure 8 représente autrement cette expérience dont la sensibilité devait permettre une mise en évidence du vent d'éther même si celui-ci est partiellement entraîné par la Terre dans son mouvement.

Malgré toutes les précautions prises et après avoir orienté le dispositif dans différentes directions, MICHELSON et MORLEY n'ont jamais pu mettre en évidence le moindre retard d'un faisceau sur l'autre. La vitesse de la lumière est la même dans toutes les directions. Ils avaient pourtant défini un système très sensible. C'est un des plus célèbres résultats négatifs de la physique.
Ce constat choquait les physiciens de l'époque car ils considéraient jusque-là que les phénomènes optiques étaient des phénomènes mécaniques dans l'éther.
Depuis, cette expérience a été renouvelée avec un plus grand luxe de précautions. Le résultat est toujours négatif.
La conclusion est inévitable même si elle va à l'encontre de l'intuition :
La vitesse de la lumière ne dépend pas de la vitesse du laboratoire dans lequel on la mesure.
Si nous associons ce résultat à la constatation que nous avons faite précédemment nous pouvons affirmer que :
Notons au passage la valeur de cette vitesse obtenue avec les moyens modernes :
- Vitesse de la lumière dans le vide = c = 299 792 458 m/s
On utilise souvent la valeur approximative c = 300 000 km/s
Allons plus loin maintenant, installons nous dans une fusée et analysons le comportement de la lumière dans une expérience d'optique embarquée (Figure 9). Quand l'astronef a un mouvement rectiligne uniforme (moteurs arrêtés), notre expérimentateur chronomètre un rayon lumineux qui se propage du point S au point M dans le but de mesurer la vitesse de propagation de la lumière.

Les faits expérimentaux précédents nous indiquent que la durée qu'il va mesurer sera toujours la même quelle que soit la vitesse (constante) de la fusée.
Observons maintenant cette expérience depuis l'extérieur (Figure 10).

Le phénomène est perçu différemment par notre observateur planétaire car pour lui les points de départ et d'arrivée se sont déplacés pendant l'expérience. C'est ce que montre la figure 11.

Comparons la distance parcourue par la lumière selon chacun des observateurs en examinant la figure 12.

L'observateur vert, depuis sa planète, constate que la lumière a parcouru la distance B pendant l'expérience. Pourtant l'observateur rouge, dans sa fusée, a mesuré une longueur de parcours A qui est plus petite que B.
Nous avons précédemment mis en évidence que la vitesse de la lumière est invariable. Donc si chacun des observateurs mesure une longueur de parcours différente, c'est que le temps ne s'écoule pas de façon absolument identique dans les deux cas ou alors que les longueurs sont modifiées par la vitesse relative des observateurs. Nous évaluerons plus loin la valeur de ces différences avec une autre "expérience de pensée" dans laquelle il sera question d'horloges à photon.
La vitesse de la lumière est une limite :
Un petit détail est à remarquer.
Considérez à nouveau l'expérience illustrée par les figures 10, 11 et 12 mais imaginez maintenant que la fusée se déplace avec une vitesse supérieure à celle de la lumière par rapport à la petite planète. C'est impossible sans remettre en cause les résultats expérimentaux qui nous ont conduits à admettre que la vitesse de la lumière est constante.
Nous pouvons ainsi comprendre que la vitesse de la lumière ne peut être dépassée ni même atteinte par des corps matériels.
La transformation de Galilée :
Avant d'avoir compris que la célérité de la lumière est une limite infranchissable, on repérait la position des objets dans des référentiels inertiels (ou référentiels galiléens) et on utilisait une transformation de Galilée pour passer de l'un à l'autre.
Un référentiel est un système de repérage dans l'espace et dans le temps. Dans un référentiel galiléen, un objet isolé est à l'arrêt ou en mouvement rectiligne uniforme quand aucune force n'agit sur lui.
Prenons l'exemple d'un train qui avance à vitesse constante et en ligne droite dans lequel un passager se déplace à vitesse constante vers l'avant (Figure 13). Nous considérons un référentiel attaché au sol (X,Y,Z) que nous nommons avec des lettres majuscules et un référentiel attaché au train (x,y,z) que nous désignons avec des minuscules.

Sur le référentiel lié au train, on définit les coordonnées du passager qui marche à partir de la position xo qu'il avait au temps origine (c'est à dire au moment t = 0).
- x = xo + Vp.t (Vp est la vitesse de déplacement du passager par rapport au train)
y = 0
z = 0 [1]
La transformation de Galilée pour passer du référentiel du train à celui du sol est très simple et on peut l'exprimer de la façon suivante en considérant que la distance entre les deux repères au moment origine (t = 0) vaut Xo :
- X = x + Vt.t + Xo (Vt est la vitesse de déplacement du train par rapport au sol)
Y = y
Z = z [2]
En combinant ces deux expressions, nous obtenons en nous référant au sol :
- X = Xo + xo + Vp.t + Vt.t = Xo + xo + t.(Vp + Vt)
Y = y
Z = z [3]
Pour calculer la composition des vitesses en passant d'un référentiel à l'autre, nous voyons que la transformation de Galilée entraîne une simple addition des vitesses, ce qui correspond tout à fait à notre intuition. Pour des vitesses appartenant à notre environnement habituel, le résultat de la transformation de Galilée semble correct... mais nous savons maintenant qu'on ne peut pas aller plus vite que la lumière, nous comprenons donc que cette formulation n'est qu'une approximation qui s'écartera de la réalité quand on l'appliquera à des vitesses comparables à la célérité de la lumière.
La figure 14 nous confronte à ce cas avec une fusée qui se déplace à la moitié de la vitesse de la lumière par rapport au sol et qui projette un obus à la moitié de la vitesse de la lumière par rapport à elle-même.

Une transformation de Galilée nous apprend que l'obus doit se déplacer à la vitesse de la lumière par rapport à l'observateur sédentaire (puisque 0,5C + 0,5C = C). Or nous savons que c'est impossible.
Avant de résoudre ce problème, je vais vous proposer une nouvelle expérience de pensée et pour étudier celle-ci avec profit, il faut connaitre le plus ancien théorème mathématique, un des plus simples à comprendre et c'est aussi celui qui est le mieux connu du grand public.
Pythagore était un mathématicien grec qui a vécu entre 570 et 495 avant notre ère. Il a enseigné le théorème que l'histoire a attaché à son nom mais cette règle mathématique était déjà connue par les plus importantes civilisations de l'antiquité. On a des raisons d'affirmer que les babyloniens l'utilisaient déjà plus de mille ans avant la naissance de Pythagore.
 Figure 15 : Un triangle rectangle
Figure 15 : Un triangle rectangle
Le théorème de Pythagore indique la relation qui existe entre les longueurs des différents côtés d'un triangle rectangle.
Considérons le triangle ABC illustré sur la figure 15. Il est rectangle en A, cela signifie que l'angle A est un angle droit (c'est à dire qu'il mesure 90°).
Le côté opposé à l'angle droit, ici nommé "a", est appelé hypoténuse. Les deux autres côtés sont les cathètes.
Pour l'usage que nous allons faire, le théorème de Pythagore peut s'exprimer de la façon suivante :
Pour la figure 15, cela donne :
- a2 = b2 + c2
 Fig 16
Fig 16
Armés de ce théorème, nous allons imaginer une horloge à photon (Figure animée 16). Elle est constituée par une cavité vide séparant deux miroirs disposés face à face et entre lesquels se propage un rayon lumineux considéré ici sous la forme d'un photon unique. Chaque miroir réfléchit ce photon vers l'autre réflecteur. Ainsi, cette onde lumineuse élémentaire fait un va-et-vient perpétuel entre les deux miroirs.
Nous savons que la vitesse de la lumière dans cette cavité vide est constante. Nous pouvons donc considérer les va-et-vient de la lumière entre les miroirs comme le tic-tac d'une horloge. Avec des miroirs espacés de 15 cm, l'aller-retour ferait 30 cm et la durée du tic-tac serait d'un milliardième de seconde. Dans ce cas, une seconde de temps correspondrait au comptage d'un milliard de tic-tacs.
Nous allons comparer les tic-tacs de deux horloges à photon identiques mais en mouvement l'une par rapport à l'autre. Pour cela, nous nous installons à côté de notre observateur sédentaire équipé d'une horloge à photon pour contempler le passage de son collègue voyageur spatial qui est équipé d'une autre horloge identique (Figure animée 17).

Sur l'horloge mobile nous constatons l'arrivée du photon sur le miroir supérieur. Il se réfléchit alors au point D. Pour l'astronaute, ce photon doit ensuite parcourir la distance DH pour atteindre le miroir inférieur.
Mais pour l'observateur sédentaire, après la durée d'un tic-tac de sa propre horloge, le photon a seulement atteint le point i et il lui faut parcourir une longueur supplémentaire avant son point de retour. Ce photon va donc parcourir la distance DA avant d'être réfléchi de nouveau.
Récapitulons :
- - Pour le voyageur, le photon parcourt la distance DH
- Pour le sédentaire, le photon parcourt la distance DA qui est supérieure à DH. Il constate aussi que le tic-tac de l'horloge mobile est plus long.
Avec le théorème de Pythagore, nous pouvons calculer le rapport des durées des deux tic-tacs constaté par l'observateur planétaire.
Considérons le triangle DHA de la figure animée 17. Pour l'observateur sédentaire, le parcours du photon entre les deux miroirs de sa propre horloge vaut la distance DH mais c'est la distance DA pour l'horloge mobile. Pendant ce trajet du photon, l'horloge mobile a traversé la distance HA.
Si nous désignons la célérité de la lumière dans le vide par la lettre c, un photon parcourt la distance DH pendant le temps t1 et il lui faut le temps t2 pour franchir la distance DA alors que pendant ce temps la fusée parcourt HA à la vitesse v. Tout ceci nous fournit les relations suivantes :
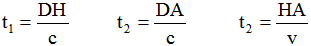 [4]
[4]Les deux dernières équations nous permettent d'associer à cette figure le rapport des vitesses entre la fusée et la lumière. Nous aurons besoin de cette relation un peu plus loin :
 [5]
[5]DHA est un triangle rectangle dont l'hypoténuse est le segment DA, nous pouvons donc utiliser le théorème de Pythagore pour affirmer que :
 [6]
[6]Ce qui équivaut à :
 [7]
[7]D'où nous déduisons :
 [8]
[8]Avec ce résultat, revenons maintenant à notre objectif qui est le calcul du rapport des durées des trajets des photons :
 [9]
[9]Simplifions cette formule en divisant le numérateur ainsi que le dénominateur par DA, cela donne l'expression équivalente suivante :
 [10]
[10]Puis en combinant cette formule avec l'expression [5] :
 [11]
[11]Ce rapport est toujours supérieur ou égal à 1. Il est très proche de 1 pour les petites vitesses (celles de notre environnement habituel) et sa valeur tend vers l'infini quand v se rapproche de c.
Cela signifie que la mesure de la durée d'un phénomène est différente selon le repère depuis lequel qu'elle est effectuée.
Nous avons obtenu cette relation en considérant les durées mais si au lieu de cela nous avions considéré les distances parcourues nous aurions trouvé le même rapport (Voir l'expression [9]). Cette expression est incontournable pour les calculs dans le cadre de la relativité.
La transformation de Lorentz :
Hendrik Antoon Lorentz était un physicien néerlandais, il est né en 1853 à Arnhem et mort en 1928 à Haarlem, toutes-deux étant des villes des Pays-Bas. A partir de la relation que nous venons d'établir, il a énoncé les formules de transformation liant deux systèmes en mouvement rectiligne uniforme l'un par rapport à l'autre.
Reprenons l'expérience du train de la figure 13 avec son passager. Avec la transformation de Galilée, la mesure du déplacement de ce voyageur par rapport au train donnait le même résultat pour un observateur au sol ou pour un observateur dans le train.
Maintenant nous savons que l'observateur depuis le sol obtiendra une valeur différente. Selon la transformation de Lorentz, il faut corriger la transformation de Galilée exprimée en [2] sous la forme "X = x + v.t" en la multipliant par le rapport précédent. Ainsi, nous obtenons :
 [12]
[12]Pour la composition des vitesses, celle du passager avec celle du train, la transformation de Galilée se contentait d'une simple addition de ces mouvements. La transformation de Lorentz nous montre que l'addition des vitesses doit être effectuée d'une manière un peu plus subtile. Voici comment les vitesses s'additionnent dans notre exemple où le passager avance dans la même direction que le train selon l'axe des X :
 [13]
[13]w' est la vitesse de déplacement mesurée dans le repère en mouvement (dans l'exemple du train, c'était la vitesse de déplacement du passager dans le train Vp).
v est la vitesse de déplacement des repères l'un par rapport à l'autre (dans l'exemple du train, c'était la vitesse du train Vt).
Bien entendu, pour les vitesses usuelles d'un train et de son passager, le résultat de la transformation de Lorentz sera quasiment identique à celui de la transformation de Galilée.
Par contre, cette transformation prend tout son sens quand on considère la fusée et son missile illustrés sur la figure 14. Dans ce cas, w' et v sont toutes deux égales à c/2 et nous obtenons :
 [14]
[14]Cela signifie que notre observateur planétaire voit le missile se déplacer avec une vitesse égale à 4/5 de c et non pas avec la vitesse de la lumière comme l'indique la transformation de Galilée.

Nous avons vu que la mesure de la durée d'un phénomène donne un résultat différent selon le référentiel depuis lequel on l'effectue. Je vous propose maintenant d'étudier les conséquences de cet aspect sur le voyage interstellaire.
Considérons le Soleil et l'étoile la plus proche de lui qui est Proxima du Centaure, elles sont séparées par la distance L = 4,243 années-lumière. Un observateur sédentaire contemple ces astres depuis une planète très éloignée, immobile par rapport aux étoiles et située à égale distance de celles-ci.
Imaginons maintenant une fusée qui entre dans le champ de notre expérience avec une vitesse "v" constante et égale à 0,9 fois la vitesse de la lumière (Figure 18). Cette fusée se déplace en ligne droite et va frôler successivement les deux étoiles.
Pour notre observateur sédentaire la durée du trajet T de la fusée entre les deux étoiles est simplement :
 [15]
[15]Mais pour le passager de la fusée cette durée aura la valeur t :
 [16]
[16]La durée du voyage est donc plus courte pour le passager de la fusée. Cette durée serait même réduite à 0,6 année si la vitesse de la fusée atteignait 99% de la vitesse de la lumière.
Ce raisonnement permet en physique des particules d'expliquer la longueur du trajet des particules instables. Les calculs selon les considérations galiléennes des longueurs de trajectoires décrites par des particules à durée de vie très courte et projetées à grande vitesse dans le vide sont toujours trop pessimistes. En fait, l'application de la transformée de Lorentz prend en compte que le temps s'écoule moins vite dans le référentiel de la particule et donc elle semble exister plus longtemps pour un observateur immobile.
- Avertissement : Les considérations que nous avons employées ici ne peuvent pas expliquer le paradoxe des jumeaux de Langevin ou le décalage des horloges atomiques qui a été étudié en faisant subir à l'une d'elles un voyage en avion alors que l'autre est restée immobile dans un laboratoire. En effet, ces problèmes appartiennent au domaine de la théorie de la relativité générale car ils concernent des référentiels dont la vitesse relative n'est pas constante.
Nous avons employé uniquement des exemples étudiables avec la relativité restreinte.
Cette étude de la vitesse de propagation de la lumière nous amène ici à nous poser des questions auxquelles la théorie de la relativité restreinte a proposé des réponses. Cette célèbre théorie initiée par Albert EINSTEIN (1879-1955) et toujours vérifiée par l'expérience, nous apprend que les longueurs sont contractées par la vitesse et que le temps ne s'écoule pas de la même façon pour deux observateurs en mouvement l'un par rapport à l'autre.
La théorie de la relativité a détruit l'idée d'un espace absolu et aussi du temps absolu. Elle a redéfini la notion de simultanéité.
La théorie de la relativité restreinte est basée sur deux postulats qu'EINSTEIN a définis en considérant les résultats expérimentaux que nous avons analysés plus haut :
- Les lois de la physique sont les mêmes dans tous les référentiels inertiels.
Dans un repère inertiel, la vitesse de la lumière c, est toujours la même, qu'elle soit émise par un objet en mouvement ou au repos.
En fait, Albert Einstein n'a pas suivi notre démarche précédente pour établir sa théorie de la relativité restreinte. Il a été guidé par l'étude de l'électricité et du magnétisme. Pour cela, il était aidé par les équations de Maxwell.

James Clerk Maxwell était un physicien écossais (1831-1879). En 1864, il présente un ensemble d'équations qui unifient l'ensemble des relations connues entre électricité et magnétisme mais l'étude des équations de Maxwell avec la physique classique aboutissait à des paradoxes... Nous allons examiner un exemple.
La figure 19 montre un fil métallique qui est parcouru par un courant électrique "i".
Conventionnellement, le courant électrique se déplace du "plus" vers le "moins". On peut considérer qu'il est composé par un flux d'électrons libres qui se déplacent dans le conducteur. Ils sont attirés par l'extrémité positive et donc ils se déplacent depuis le "moins" vers le "plus", c'est à dire en sens inverse du sens conventionnel du courant.
Rappelons que la matière est composée d'atomes eux-mêmes constitués par des noyaux qui ont une charge électrique positive et qui sont entourés d'un certain nombre d'électrons chargés négativement. La plupart du temps, chaque électron est associé à un noyau autour duquel il tourne et dont il ne s'éloigne pas.
Toutefois, des électrons libres sont communs dans les métaux, ils ne sont pas fermement liés aux atomes et ils peuvent se déplacer sous l'effet d'un champ électrique. Ces métaux sont donc conducteurs d'électricité.
L'expérience (ainsi que les équations de Maxwell) nous apprend qu'un courant électrique engendre un champ magnétique. Dans la figure 19, le courant engendre un champ magnétique B qui entoure le conducteur et qui est représenté par des flèches rouges.
Imaginons maintenant un fil parcouru par un courant électrique et électriquement neutre, c'est à dire que les charges électriques négatives qu'il contient compensent exactement ses charges électriques positives. Une particule chargée négativement se déplace près du fil et parallèlement à lui. Pour simplifier nos réflexions nous considèrerons qu'elle se déplace à la même vitesse et dans le même sens que les électrons libres qui composent le courant dans le fil. Nous savons qu'une telle particule chargée en mouvement dans un champ magnétique voit sa trajectoire incurvée mais nous allons examiner cette situation avec deux référentiels différents.

Référentiel sur le fil :
Le fil est électriquement neutre. Si nous considérons le tronçon de fil coloré sur la figure 21, cela signifie que le champ électrique généré en ce lieu par les charges négatives des électrons libres qui constituent le courant est équilibré par les charges du reste de la matière du fil dont la résultante est positive.
Nous appellerons ρ (- ou +) la densité des charges électriques (négatives ou positives) ou, si vous préférez, la quantité de charges électriques par unité de volume.

Le champ magnétique est perpendiculaire à la figure.
Puisque le fil est électriquement neutre, il n'exerce aucune force électrique sur notre particule. Toutefois, celle-ci est déviée par le champ magnétique, elle subit une force F dirigée vers le fil :
- F = q.Vo.B [16]
La trajectoire de la particule est déviée vers le fil par le champ magnétique.
Référentiel sur la particule :
Maintenant la particule est fixe et c'est le fil qui se déplace vers la gauche de la figure. Les électrons libres du courant sont donc fixes par rapport au référentiel et ce sont les charges positives liées au fil qui vont générer un champ magnétique.
Or la particule est ici au repos, il n'y a donc pas de force magnétique qui agit sur elle puisque cette force est proportionnelle à la vitesse. Comment pouvons-nous alors expliquer la cause du rapprochement entre le fil et la particule ?
Puisque qu'il n'y a pas de force magnétique, ce rapprochement ne peut être dû qu'à une force électrique... Comment cela se peut-il puisque le fil est électriquement neutre ?
En fait, il était électriquement neutre pour notre référentiel précédent.
On pourrait rechercher la solution de notre problème dans une variation de la charge électrique causée par le déplacement mais nous n'aboutirions pas. En effet, la valeur d'une charge électrique n'est pas modifiée par le mouvement. Ceci est facile à démontrer car on ne constate pas une variation de la charge électrique d'un matériau quand on le chauffe. Pourtant cet échauffement provoque une agitation des atomes et des particules chargées qui le composent. Les masses des électrons chargés négativement et celles des noyaux chargés positivement sont très différentes et par conséquent leurs vitesses varient dans des proportions différentes. Si les valeurs des charges électriques étaient influencées par le mouvement alors la charge électrique de ce matériau évoluerait d'une façon très significative. Or cela n'arrive pas.
La charge électrique d'une particule est invariante et indépendante du référentiel.
Si la charge des particules ne varie pas, qu'en est-il de la densité des charges ?
Rappelons ce que nous avons vu précédemment : La vitesse de déplacement contracte les longueurs.
Nous allons considérer séparément dans le fil les électrons libres du courant électrique et la matière chargée positivement. Dans le cas précédent le courant se déplaçait par rapport au référentiel alors que maintenant c'est l'ensemble des charges positives.
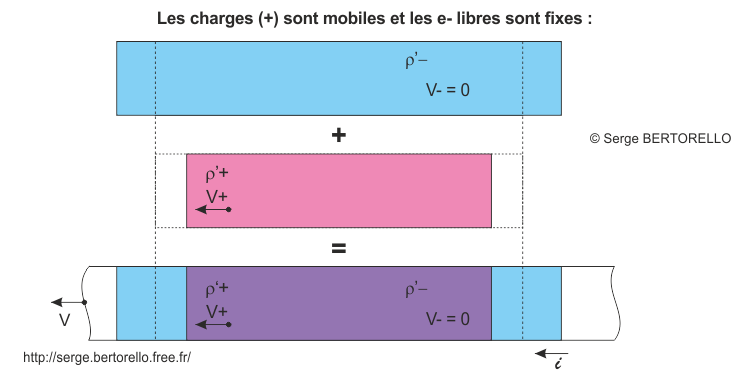
Les charges électriques ne sont plus équilibrées.
Les électrons libres (immobiles par rapport à notre particule) contenus dans le tronçon que nous considérions précédemment sont maintenant répartis sur un plus grand volume. En effet, leur mouvement dans le référentiel du fil contractait la longueur de leur section. Le changement de référentiel diminue donc la densité de leurs charges.
Par contre la partie positivement chargée est maintenant contractée par la vitesse et sa densité augmente.
La densité des charges négatives a baissé et celle des charges positives a augmenté. Par conséquent le fil en mouvement apparaît chargé positivement dans le référentiel de la particule et c'est une force électrique qui rapproche ces deux éléments.
Minute papillon !
A ce moment de mon exposé, il apparaît généralement une agitation dans l'assistance. Souvent une personne s'exclame sur un ton indigné :
- Mais êtes-vous en train de démontrer que le champ magnétique n'existe pas ? J'ai pourtant reçu un enseignement scolaire sur le champ magnétique...
A quoi je réponds en approuvant :
- Oui... moi-aussi j'ai étudié le champ magnétique. Je me rappelle du bonhomme d'Ampère ou de la règle des trois doigts de la main droite...
Un autre s'exclame sur un ton plutôt agressif :
- Sur une page de votre site web, vous expliquez le fonctionnement d'un canon à électrons en évoquant la "déflection magnétique" de ces particules et là vous nous expliquez que le champ magnétique n'existe pas. Vous vous contredisez... vous êtes incohérent...
En tant que marseillais, j'ai alors envie de répondre "Bouleguès pas pichoun !", une expression provençale qui peut se traduire par "Calme-toi petit !"
J'ai aussi envie d'ajouter que la démonstration n'est pas de moi...
Les physiciens expriment cette situation paradoxale en disant d'une façon diplomatique :
- Electricité et magnétisme sont deux façons de voir la même chose.
Notez aussi que lorsque l'on dénombre les différentes forces qui existent dans l'univers, dans le cadre du modèle standard, on ne cite jamais la force magnétique. On cite seulement les quatre forces suivantes : force gravitationnelle, force électrique (ou électromagnétique), interaction nucléaire faible et interaction nucléaire forte.
Le physicien russe Pavel Cherenkov (1904–1990) a obtenu un prix Nobel en 1958 pour avoir découvert et interprété l'effet qui porte son nom.

© IRSN (cliquer sur l'image pour accéder au site web original).
L'effet Cherenkov se produit lorsqu'une particule se déplace plus vite que la lumière dans un milieu. Sa vitesse n'est toutefois pas plus rapide que celle de la lumière dans le vide, ceci ne contredit donc pas notre précédent résultat.
Prenons l'exemple de l'eau : dans ce corps la lumière se propage à la vitesse de 226000 km/s. Considérons une particule qui pénètre dans ce liquide avec une vitesse de 280000km/s, celle-ci est inférieure à la célérité de la lumière dans le vide mais cette particule se déplace plus vite que la lumière dans l'eau, il apparaît alors un rayonnement Cherenkov causé par l'onde de choc de la particule rapide au sein de la matière.
L'effet Cherenkov est utilisé pour mettre en évidence les particules rapides.
C'est l'effet Cherenkov qui explique la lueur bleutée que l'on peut voir dans la piscine des réacteurs nucléaires. En effet, des particules sont émises avec de très grandes vitesses dans le cœur du réacteur nucléaire puis elles sont ralenties par l'eau environnante en émettant un rayonnement bleu.
Dans l'espace, les astronautes peuvent observer l'effet Cherenkov quand des particules rapides du rayonnement cosmique traversent les liquides physiologiques de leurs yeux. Ils perçoivent de temps en temps des éclairs bleus.
Je vous invite à lire :
- "Léon Foucault" de William TOBIN édité par EDP Sciences.
- "Hippolyte Fizeau, physicien de la lumière" de James LEQUEUX édité par EDP Sciences.
- "Le cours de physique de Feynman" de Richard Feynman, Robert B. Leighton et Matthew Sands réédité par Dunod.

