Le support du miroir primaire d'un télescope
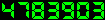

Les flexions du miroir primaire
Après avoir soigneusement surfacé le miroir principal de notre télescope vient le moment de le disposer dans le barillet. Il s'agit du dispositif qui va le maintenir au fond du tube tout en permettant un réglage précis de son orientation.
Idéalement, le miroir doit reposer sur ce support sans subir la moindre déformation.
Du point de vue de la mécanique, la position et l'orientation du miroir seront parfaitement déterminées si le dos de celui-ci repose sur trois points d'appui et si sa tranche est positionnée par deux autres points d'appui (figure 1).
En pratique, il faut compter avec les flexions du miroir.
La surface "utile" de ce composant d'optique astronomique a été obtenue avec une très grande précision. Par convention, on exprime habituellement cette dernière en comparant les plus grosses déformations du front d'onde fourni par cet objectif à la longueur d'onde qui caractérise le rayonnement auquel l'il humain est le plus sensible en vision diurne. Cette valeur de référence est notée avec la lettre grecque λ (lire "lambda"). λ = 560 nm
"nm" est l'abréviation de nanomètre. 1 nm vaut un milliardième de mètre ou un millionième de millimètre. La règle de Rayleigh : Lord Rayleigh (=John William STRUTT 1842 - 1919) a démontré que l'objectif fournit une bonne image de diffraction si l'onde lumineuse qu'il transmet est comprise entre deux sphères concentriques espacées par λ/4 au maximum (dans cette expression, la barre inclinée désigne le trait de fraction).
λ/4 = 560/4 = 140 nm
On exprime plus couramment cette règle en disant que l'écart maximum du front de l'onde émergente doit être inférieur à λ/8 par rapport au front d'onde moyen. Certains défauts de l'onde auront un écart positif jusqu'à +λ/8 et d'autres auront un écart négatif jusqu'à -λ/8. D'un extrême à l'autre, l'amplitude totale des défauts vaut donc bien λ/4 (figure 2). λ/8 = 560/8 = 70 nm
En fait, pour obtenir des images de bonne qualité et pour limiter l'influence de la turbulence atmosphérique, il est préférable que les miroirs soient réalisés avec une meilleure précision. Souvent, l'opticien cherche à obtenir des miroirs dont les plus gros défauts du front d'onde sont inférieurs à λ/16. Pour le sujet qui nous occupe ici, il est important de se rappeler que les déformations du front de l'onde émergeant d'un miroir sont deux fois plus grandes que les défauts de la surface de ce miroir (figure 3). Conventionnellement, l'opticien doit évoquer les défauts du front d'onde lorsqu'il expose la précision d'un miroir. Pourtant, certains commerçants citent la précision de la surface du miroir lui-même, c'est plus flatteur pour leur produit.
Les flexions du miroir dans son barillet : Bien entendu, il faut que le barillet maintienne le miroir au fond du tube sans lui faire subir de contrainte susceptible de dégrader la précision de sa surface mais il faut ajouter à cela que le miroir fléchit sous son propre poids entre les points d'appui. Par conséquent, le barillet doit être conçu pour limiter ces flexions à des valeurs acceptables. Les flexions d'un disque sous son propre poids sont proportionnelles au rapport R4/e2. Dans cette expression, "R" représente le rayon du miroir et "e" représente son épaisseur. Cela signifie qu'un miroir de 15cm de diamètre et 2cm d'épaisseur présente la même flexion sous son propre poids qu'un autre miroir fait dans le même matériau qui aurait 30cm de diamètre et 8cm d'épaisseur (en effet, dans ces deux cas le rapport R4/e2 est égal à 791cm2). Bien entendu, pour que la comparaison des flexions de ces deux miroirs soit possible il faut qu'ils aient des supports semblables. Nombre de points d'appui :
La figure 1 nous montre un miroir qui repose sur trois points d'appui. Ce type de support convient très bien aux petits miroirs car ils fléchissent peu sous leur propre poids. Toutefois, les gros miroirs (diamètre supérieur à 300mm) n'ont habituellement pas une épaisseur suffisante pour limiter les flexions qu'ils auraient sur un support à trois points d'appui. La solution la plus employée pour limiter ces flexions consiste à multiplier le nombre de points d'appui. Ainsi, le miroir de 400mm de diamètre du télescope "Hercule" de l'AMAS repose sur six points d'appui. D'autres instruments possèdent des barillets à 9 points d'appui voire plus. Le logiciel PLOP : Dans un article intitulé "Mirror Support: 3 or 9 Points?" et publié dans la revue SKY & TELESCOPE en septembre 1994, Toshimi Taki a présenté les résultats de son étude sur les flexions des miroirs. Pour cela, il a modélisé le miroir dans un logiciel avec la méthode des éléments finis. Son étude ainsi que les éléments logiciels qu'il a écrits ont été utilisés par David LEWIS pour réaliser son logiciel PLOP. Ce logiciel montre les flexions que subit sous son propre poids un miroir dont on indique les caractéristiques et le type de barillet. Les résultats que je vais vous exposer ont été obtenus avec le logiciel PLOP. Je vous propose d'examiner les flexions d'un miroir en Pyrex de 200mm de diamètre, 1m de distance focale et de 32mm d'épaisseur, il est posé horizontalement sur les points d'appui. Pour celui-ci, le rapport R4/e2 vaut environ 1000cm2, il sera donc très facile d'extrapoler les valeurs de ses flexions à d'autres miroirs. Par exemple : un miroir utilisé dans les mêmes conditions et pour lequel le rapport R4/e2 vaut 2500cm2 présentera des flexions 2,5 fois plus importantes car 2500 / 1000 = 2,5. 3 Points d'appui sur le bord du miroir : Considérons le cas illustré par la figure 4. Trois points d'appui sont situés sur le bord du miroir.
Avec le logiciel PLOP, j'ai étudié la déformation de ce disque de verre sous son propre poids. Comme on pouvait s'y attendre, j'ai constaté que le centre du miroir s'est affaissé ainsi que le bord entre les points de contact. La figure 5 montre la déformation du miroir le long d'un diamètre qui passe par un point d'appui (courbe bleue).
Le bord opposé au point d'appui s'est affaissé de 36 nm, mais c'est le centre qui a descendu le plus avec 53 nm. L'amplitude de la déformation est la différence de hauteur entre le point le plus élevé (le pic) et le point le plus bas (la vallée). Ici, la déformation pic-vallée (P-V) vaut 53 nm. Comme nous l'avons vu plus haut, elle entraîne un défaut d'amplitude double sur la sphéricité de la surface d'onde, soit 106 nm. Cela représente un défaut d'environ λ/5 de la surface d'onde (car 560/106 est environ égal à 5). Globalement, cette déformation a accentué la concavité du miroir et elle a diminué la distance focale de 21µm (ou 0,021 mm). C'est insensible mais si nous comparons le nouveau profil du miroir à celui qui correspond à cette nouvelle distance focale, le résultat est amélioré. Cela revient à comparer la déformation sur la figure 5 à la parabole de la meilleure onde de référence (en vert). L'écart devient 36 nm ce qui représente 72 nm sur l'onde (c'est à dire environ λ/8).
3 Points d'appui à 65% du rayon : L'expérimentation avec le logiciel PLOP de diverses dispositions de miroirs nous enseigne que la position des points d'appui sur le bord n'est pas la meilleure. Avec un support à 3 points d'appui, ce logiciel nous démontre que les déformations du miroir causées par son propre poids sont minimales quand les points d'appui sont situés à une distance au centre qui vaut environ 65% du rayon du miroir. La figure 4 illustre ce cas. La figure 7 nous montre la déformation de ce disque de verre sous son propre poids. Elle à une amplitude pic-vallée égale à 13nm, elle est donc bien plus faible que la précédente. Le plus grand écart à la parabole de la meilleure onde de référence atteint seulement 11nm. Ceci correspond à une déformation de l'onde de λ/25 (La déformation du front d'onde est égale à 11x2 = 22nm, 560/22 = 25).
Cette disposition des trois points d'appui me semble donc bien préférable pour supporter un miroir principal de télescope. Epaisseur minimale d'un miroir reposant sur 3 points :
Dans le cas optimum que nous venons d'examiner et lors des observations au zénith, la surface de notre miroir s'écarte de 11nm de l'idéal ce qui représente une déformation de l'onde de λ/25. Je pourrais accepter un défaut deux fois plus important. Une autre façon d'exprimer cette tolérance consiste à affirmer que le rapport R4/e2 doit valoir au maximum 2000 (avec R et e exprimés en cm).
6, 9 Points d'appui ou plus : Les grands miroirs ne peuvent pas avoir une épaisseur suffisante pour limiter les flexions à des valeurs acceptables. Considérons par exemple un miroir de 400mm de diamètre qui respecterait le critère [R4/e2 inférieur ou égal à 2000cm2], il devrait avoir environ 9cm d'épaisseur. D'autres cas peuvent être plus inquiétants comme un miroir de 600mm qui devrait être épais de 20cm, il pèserait plus de 140kg! Il faut limiter l'épaisseur des miroirs à des valeurs acceptables pour un équilibrage thermique rapide, un coût limité, pour leur manipulation ou leur transport. Par conséquent, les miroirs de gros diamètre sont trop fins pour accepter un support à trois points d'appui. Il faut donc concevoir un barillet avec un plus grand nombre de points d'appui. Pour étudier les flexions de ces miroirs et optimiser leur barillet, je vous recommande d'utiliser le logiciel PLOP. Le poids du miroir doit être réparti de façon maîtrisée sur l'ensemble des points d'appui tout en préservant les possibilités de réglage de son orientation. Quand 6 points d'appui sont nécessaires, il suffit de placer sur chaque vis de réglage un balancier qui supporte le miroir par ses extrémités (voir ci-après le barillet de Hercule). Pour obtenir 9 points d'appui, à la place de ces balanciers on utilise des pièces triangulaires qui appuient par leurs trois sommets sur le dos du miroir. Une autre solution pour augmenter le nombre de points d'appui consiste à utiliser des "leviers astatiques", dans ce cas la pression sur le point de contact est appliquée par une extrémité d'un balancier (le levier), à l'autre extrémité se trouve un contre poids. Ainsi, la pression dépend bien de l'orientation de l'instrument. Je vous invite à étudier une description plus détaillée de ces solutions dans le célèbre ouvrage d'André Danjon et André Couder "Lunettes et télescopes". Les miroirs minces : Quand l'épaisseur du miroir est si faible que le rapport R4/e2 est supérieur à 30000cm2, le miroir devient très "flexible" à l'échelle des défauts que nous cherchons à éviter. Dans ce cas, quand le télescope n'est pas pointé vers le zénith, le miroir se déforme en s'appuyant sur les points d'appui de sa périphérie. Il "plie" autour de son diamètre horizontal et il peut alors être affecté par un astigmatisme sensible que certains appellent "astigmatisme de pliure". Sa distance focale se raccourcit selon le diamètre vertical et s'allonge selon le diamètre horizontal. TITAN = Télescope D=145mm F/D=4,77 : Ce petit télescope est présenté en détail sur d'autres pages de ce site. Lorsque j'ai fabriqué TITAN, je n'étais pas autant informé sur les flexions des miroirs et j'ai conçu son barillet sans précautions particulières sur ce point. Voici le plan de son barillet :
Les points d'appui se situent à 65mm de l'axe (soit 0,9 R), le miroir est en verre à vitre, il a une épaisseur de 18mm ce qui donne R4/e2 = 850cm2. Le logiciel PLOP nous apprend que la déformation de la surface d'onde imputable aux flexions du miroir sous son propre poids atteint 44nm lors de l'observation au zénith. Cela correspond à un défaut de λ/13 qui est sans conséquence sensible. Cet exemple montre que les petits miroirs peuvent tolérer des barillets mal optimisés. PEGASE = Télescope D=252mm F/D=4,6 : Ce magnifique télescope appartient à Sauveur LISCIANDRA, il possède un tube carré en bois. Son barillet a été optimisé, ses trois points d'appui sont situés à 65% du rayon. Voici le plan de son barillet :
Le miroir principal de PEGASE, en Pyrex, a une épaisseur de 47mm, pour celui-ci R4/e2 = 1150cm2. Avec ce barillet, la déformation du miroir sous son propre poids est inférieure à 13nm soit 26nm sur l'onde, c'est à dire λ/21. C'est excellent. Ce barillet n'a pas été étudié avec Plop, il n'a pas été optimisé. Les 6 points d'appui sont constitués par des disques en téflon de 2mm d'épaisseur placés aux extrémités de 3 balanciers. Ainsi la pression exercée par chacune de ces cales est la même. Ces points d'appui se situent à 93% du rayon. Avec ce barillet, la déformation du miroir sous son propre poids corrigée de la courbure d'ensemble du miroir est inférieure à 14nm soit 28nm sur l'onde, c'est à dire λ/20. C'est très bon et cet instrument nous fournit de fabuleuses images planétaires... quand la météo est favorable.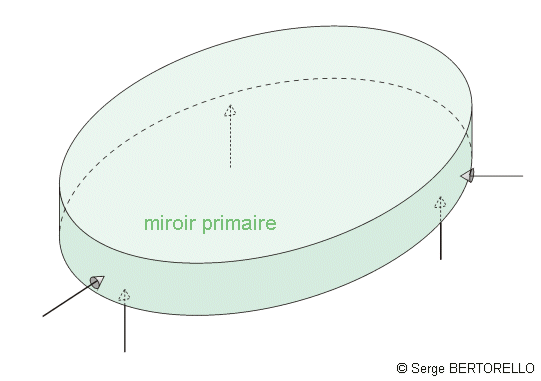




D=200mm, e=32mm, R4/e2 = 1000 cm2
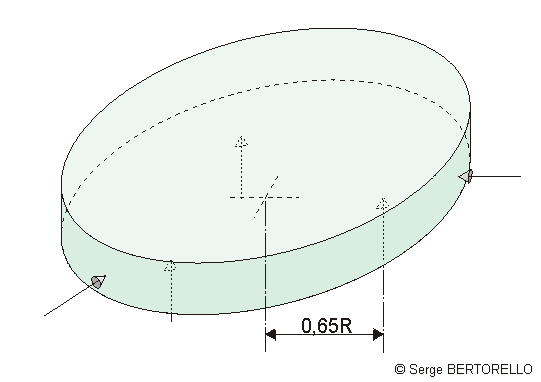

D=200mm, e=32mm, R4/e2 = 1000 cm2


Le télescope PEGASE fournit de superbes images planétaires.
HERCULE = Télescope D=406mm F/D=4,6 : Ce télescope appartient à notre association AMAS. Il n'est pas installé sur un poste fixe, il est démontable et nous le transportons à l'arrière d'un véhicule de tourisme. Il possède un tube en bois, carré et largement dimensionné. L'épaisseur du miroir vaut 76mm, ce qui lui confère un rapport R4/e2 = 2940cm2.


