NOTIONS D'OPTIQUE

Comparaison des télescopes à deux miroirs avec le Newton

Nous allons comparer ici la finesse des images obtenues avec les combinaisons présentées plus haut. Toutefois, il faut être bien conscient qu'on ne peut pas définir un jugement tranchant et définitif car les propriétés de chaque formule varient énormément en fonction des caractéristiques choisies.

De toute façon, il n'y a pas de meilleur télescope, chaque solution est un compromis qui peut être avantageux ou pas selon les besoins de l'utilisateur.

Nous allons tout d'abord considérer un télescope décrit en page 196 du célébrissime livre écrit par André Danjon et André Couder intitulé "Lunettes et télescopes" et nous allons le comparer aux autres formules en prenant des caractéristiques semblables.

Le résultat est présenté sur la figure suivante.

Figure 26 : Comparaison de la finesse des images de différentes formules de télescopes.
D = 800mm     F = 6400mm     F/D = 8
Pour le Newton : le miroir plan a un petit côté de 95mm et il est placé à 600mm du foyer.
Autres combinaisons : f₁ = 4880mm   e = 200mm   γ = 1,31   diamètre du secondaire = 361mm
Graphiques réalisés à l'aide du logiciel CORRECT 3.

On remarque tout d'abord sur les lignes pointillées du haut que la luminosité du Newton est proche de 100% (plus exactement 98,6%) car il est peu obstrué par le miroir plan. Par contre, les combinaisons Cassegrain ont une luminosité inférieure à 80% due à une obstruction de 0,45 (sur le diamètre) ce qui est considérable. Cette forte obstruction centrale n'est pas favorable aux observations planétaires.

L'instrument qui a le champ le plus étendu est le Ritchey-Chrétien. La courbe qui caractérise la finesse de ses images suit une courbe parabolique caractéristique de l'astigmatisme.

Les courbes des autres instruments sont presque droites, ce qui signifie que c'est la coma qui est prépondérante.

Notons aussi que pour cette configuration le Dall-Kirkham n'est pas beaucoup plus mauvais que le Cassegrain et le Newton.

Etudions maintenant une autre disposition avec un grandissement supérieur pour le secondaire.

Figure 27 : Comparaison de la finesse des images de différentes formules de télescopes.
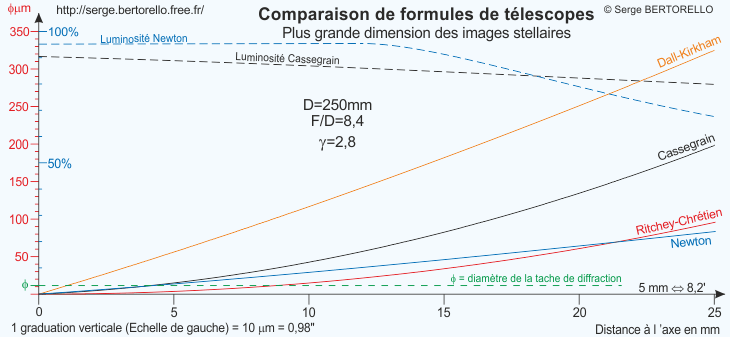
D = 250mm     F = 2100mm     F/D = 8,4
Pour le Newton : le miroir plan a un petit côté de 50mm et il est placé à 220mm du foyer.
Autres combinaisons : f₁ = 750mm    e = 100mm    γ = 2,8     diamètre du secondaire = 75mm
Graphiques réalisés à l'aide du logiciel CORRECT 3.

Il est important de noter que l'échelle de gauche n'est pas la même que sur le graphique précédent.

Le Newton a encore une obstruction plus faible, cette fois elle vaut 0,2 sur le diamètre.

J'ai défini les formules Cassegrain pour avoir une obstruction égale à 0,3, celle-ci est raisonnable.

Avec cette disposition, on retrouve le même classement selon les performances que précédemment mais le Dal-Kirkham possède cette fois-ci un champ nettement moins bon et les performances du Newton voisinent celles du Ritchey-Chrétien.

Ces deux exemples montrent qu'il n'est pas possible de définir a priori les performances d'un télescope et qu'il faut être prudent en préjugeant les mérites ou les défauts d'un type de télescope.

Les télescopes que nous avons examinés précédemment sont par principe strictement achromatiques et stigmatiques sur leur axe pour l'observation des objets très éloignés. Ce ne sera plus le cas avec les formules que nous allons examiner maintenant car elles sont constituées par une combinaison de réfraction et de réflexion.