NOTIONS D'OPTIQUE

POUR LES ASTRONOMES AMATEURS

Le miroir principal du télescope de Newton

Pour obtenir une image parfaite d'un point situé à l'infini au foyer d'un miroir utilisé comme objectif, il faut que celui-ci soit concave et que sa méridienne (son profil) ait la forme d'une parabole. On devrait alors dire que la surface utile du miroir a la forme d'un "paraboloïde de révolution" mais on dit usuellement que le miroir est "parabolique". Cette forme est caractérisée par le coefficient de déformation b = -1.

Pour qu'il puisse fournir la meilleure image possible, on démontre que les plus gros défauts de surface du miroir principal d'un télescope doivent être inférieurs à 1/8 de la longueur d'onde de la lumière utilisée. On dit que les défauts sur le verre doivent être inférieurs à λ/8 (lambda sur huit). Pour les observations visuelles, on considère le maximum de sensibilité de l'œil qui se situe vers la longueur d'onde de 0,56µm. Sur un objectif réfracteur, la précision requise sur le verre est quatre fois moindre (λ/2 est suffisant) mais il faut usiner quatre surfaces (au lieu d'une seule pour l'objectif réflecteur).

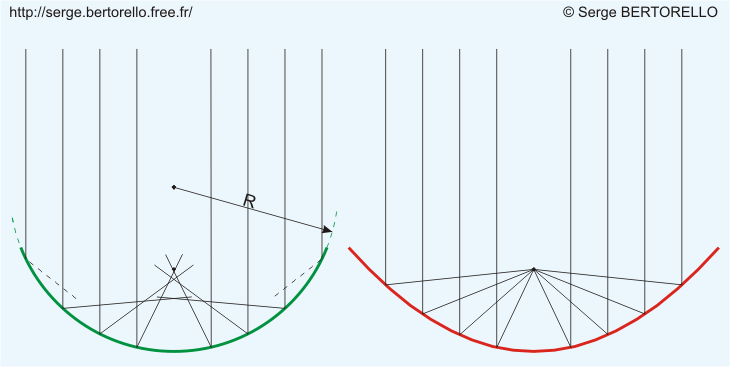
La distance focale F d'un miroir parabolique vaut la moitié du rayon de courbure R de la sphère qui est tangente à son sommet.

     [14]

Près de son sommet, ce paraboloïde est proche de la sphère tangente surtout pour les faibles ouvertures (grandes valeurs du rapport F/D). Or la sphère est la forme la plus facile à obtenir pour une surface optique. C'est pour cela qu'on trouve dans le commerce des télescopes de Newton avec miroir sphérique. Par conséquent ces miroirs économiques possèdent une aberration de sphéricité.

Figure 17 : Comparaison entre une parabole et le cercle tangent en son sommet.

Figure 18 : Aberration de sphéricité d'un miroir sphérique (à gauche) et stigmatisme du miroir parabolique de même distance focale (à droite) pour la formation de l'image d'un point situé à l'infini.

Le coefficient de l'aberration de sphéricité d'un miroir sphérique lorsqu'il forme l'image d'un objet très éloigné vaut :

     [15]

Appliquons cette valeur de S dans les formules [5] et [6] que nous avons exprimées plus haut en considérant que h représente le rayon du miroir. Nous déduisons l'aberration longitudinale du miroir sphérique :

     [16]

Il est intéressant de constater qu'elle est égale à la moitié de la flèche de courbure du miroir.

Nous déduisons aussi l'aberration transversale t et le rayon r du cercle de moindre aberration :

     [17]
     [18]

Si la distance focale est assez grande, le miroir sphérique peut fournir une bonne image d'un objet éloigné. La formule suivante nous indique sa distance focale minimale F (en millimètres) en fonction du diamètre D (en millimètres lui aussi) pour atteindre ce but (avec λ=0,56µm) :

     [19]

Exemple : Cette formule nous apprend qu'un miroir sphérique de 150mm de diamètre doit avoir une distance focale au moins égale à 1210mm pour pouvoir être employé comme miroir primaire sur un télescope de Newton.

En fait, la sphère est la meilleure forme pour un miroir qui doit former l'image d'un objet situé en son centre de courbure. Si on éloigne l'objet, la méridienne idéale de ce réflecteur devient alors une ellipse pour laquelle l'objet et l'image occupent chacun un foyer. Si on éloigne encore l'objet, il faut étirer l'ellipse jusqu'à ce qu'elle devienne une parabole quand l'objet est repoussé à l'infini, l'image nette et sans aberration de sphéricité est alors située au foyer de cette courbe.

Le miroir parabolique fournit une image parfaite d'un point infiniment éloigné sur son axe. Dès qu'on s'écarte de l'axe, on constate l'apparition des aberrations extra-axiale comme la coma. Le coefficient de coma d'un miroir parabolique est positif car la coma est extérieure, il vaut :

     [20]

Appliquons cette valeur à la formule [7] et nous déduisons l'expression suivante qui nous donne la longueur de l'aigrette de coma au foyer du miroir parabolique d'un télescope de Newton :

     [21]

Habituellement, un télescope de Newton a un rapport d'ouverture F/D inférieur à 10. Dans ces conditions, la coma est la principale aberration extra-axiale. Cela signifie que c'est la coma qui limite l'étendue du champ exploitable au foyer d'un télescope de Newton.

Quand il commence à devenir sensible, l'astigmatisme modifie l'apparence de l'aigrette comme le montre la figure 19.

Figure 19 : Images d'étoiles obtenues avec un télescope de Newton loin de l'axe optique qui est à gauche de l'image. La distance à l'axe de l'image de droite vaut le double de celle de gauche.

Le lieu de la focale sagittale est le plan focal lui-même alors que celui de la focale tangentielle est une sphère dont le rayon vaut la moitié de la longueur focale. L'image de moindre aberration se forme sur une sphère dont le rayon vaut la longueur focale.

On déduit que le coefficient d'astigmatisme d'un miroir parabolique vaut :

A = +1     [22]

Le télescope de Newton est un instrument relativement universel car il peut être employé efficacement pour les divers types d'observation (fort ou faible grossissement, visuel ou photographique). Il est relativement compact et sa fabrication est aisée.

Certaines critiques dirigées vers cet instrument concernent sa courte distance focale peu propice aux forts grossissements nécessaires pour l'observation des planètes ou des étoiles doubles. Je réponds à cet argument en proposant l'utilisation d'une bonne lentille de Barlow, c'est un accessoire d'emploi très courant.