Dimensions du miroir plan d'un télescope de Newton
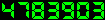
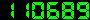
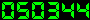
Le constructeur d'un télescope de Newton est tôt ou tard confronté au calcul des dimensions du miroir secondaire.
Sur une autre page de ce site, je vous propose la description d'une technique de réalisation d'un miroir plan.
Le lecteur qui serait inquiété par les expressions mathématiques contenues dans cet article pourra consulter avec profit la page sur les notions de mathématiques.
La figure suivante illustre le schéma optique d'un télescope de Newton.

D = diamètre du miroir principal
d = diamètre du champ de pleine lumière
p = distance du foyer à l'axe optique du miroir principal
a = petit côté du miroir plan
Le point F désigne le foyer du miroir principal
La distance "p" entre le foyer et l'axe optique du miroir principal est définie lors de la conception du télescope à partir des dimensions du tube de l'instrument et de la position souhaitée pour l'image focale. Il faut en effet que ce foyer soit accessible par les équipements d'observation tels que oculaire, boîtier photographique, caméra électronique...
Le champ de pleine lumière indique la taille maximum du champ observé qui n'est diaphragmé par aucun obstacle. Dans un télescope de Newton, c'est le bord du miroir plan qui va limiter ce champ... si on prend bien soin de ne pas occulter le bord du faisceau lumineux avec d'autres limites (comme le bord du porte oculaire).
L'intersection du miroir plan avec le cône de lumière issu du miroir principal a une silhouette en forme d'ellipse, c'est donc idéalement cette forme qui doit délimiter le miroir plan comme le montre la figure 2.

"b" est le grand côté du miroir plan. Pour le déterminer, il suffit de multiplier la valeur du petit côté par la racine carrée de 2.
[formule 1]
Dans la suite du texte, nous nous intéresserons surtout au petit axe de l'ellipse.
Dans ce cas le champ de pleine lumière est ponctuel (d=0) et l'expression qui donne "a" est très simple :
[formule 2]
Habituellement, on considère que le champ de pleine lumière doit avoir la dimension de l'image de la lune au foyer de l'instrument. Le diamètre apparent de cet astre est de 1/2 degré. Nous pouvons donc facilement calculer la taille de son image au foyer, nous l'appellerons "d" car ce sera aussi la taille du champ de pleine lumière :
d = tangente(0,5°).f = 0,0087.f [formule 3]
Calculons maintenant le petit côté du miroir plan pour ce champ de pleine lumière :
[formule 4]
Notez aussi la formule inverse qui permet de trouver la taille du champ de pleine lumière quand on connaît les dimensions du miroir secondaire.
[formule 5]
Vous savez maintenant comment calculer la dimension du miroir plan, il vous faudra aussi le placer correctement dans le tube du télescope. Il peut sembler évident qu'il faut placer le centre optique du miroir plan précisément sur l'axe du miroir principal ainsi que sur l'axe de l'oculaire mais ce n'est pas la position idéale. Sur une autre page, je vous propose de déterminer sa meilleure position sur un télescope de Newton.
Exemples :
Pour illustrer l'emploi de ces équations mathématiques, je vous propose de considérer mon télescope TITAN dont vous pouvez voir les plans détaillés sur une autre page.
Les caractéristiques de TITAN sont : D = 145mm, f=691,5mm, p=152,5mm
La formule 2 nous permet de calculer la valeur minimale de "a" pour d=0 :
Si nous souhaitons que le champ de pleine lumière puisse contenir la Lune, nous prendrons la valeur suivante pour "d" que nous fournit la formule 3 :
d = tangente(0,5°).691,5 = 0,0087 x 691,5 = 6mm
En utilisant cette valeur dans la formule 4, nous obtenons :
En fait, j'ai équipé ce télescope avec un miroir plan de 41mm de petit côté. La formule 5 nous permet de calculer le champ de pleine lumière effectif de TITAN :
Grâce à la formule 1, nous pouvons calculer la dimension du grand axe de ce miroir :
Celui qui veut réaliser des photographies au foyer de cet instrument peut souhaiter en savoir plus sur l'évolution de l'assombrissement au bord du champ. Pour cela, je vous propose d'utiliser mon logiciel CORRECT 3 Celui-ci analyse les diverses performances d'un télescope de Newton. Il fournit notamment la courbe d'assombrissement de l'image focale en fonction de l'éloignement de l'axe.

La courbe de l'assombrissement ne débute pas à 100% car le miroir plan occulte toujours une part du faisceau incident. C'est ce qu'on appelle l'obstruction. Ce graphique nous permet de déduire que la luminosité dans les coins d'un cliché 24x36 (à 21,6mm de l'axe) exposé au foyer de cet instrument serait d'environ 50% de la luminosité sans obstruction. Les angles de la photo seront donc sous-exposés.
Les formules que nous venons d'étudier donnent de bon résultats pour les télescopes "conventionnels" mais dès qu'on considère des instruments "exotiques" elles peuvent être complètement erronées. Par exemple, avec un rapport F/D = 1, ces relations fournissent des résultats aberrants.
Ce type d'ouverture improbable se rencontre plutôt dans le domaine de la radioastronomie. Toutefois, pour un télescope optique de grande ouverture, disons avec un rapport F/D inférieur à 4, il faut tenir compte dans nos calculs du fait que le miroir plan ne doit pas être centré sur l'axe (voir la page sur la position du miroir plan sur un télescope de Newton).
Il faut aussi considérer la courbure du miroir principal qui relève ses bords par rapport à son centre.
Pour exprimer la dimension minimale du petit côté du miroir plan d'un télescope de Newton, nous en arrivons ainsi à la relation suivante qui est plus complexe mais elle est exacte :
[formule 6]
La lettre "e" désigne ici la flèche de courbure du miroir, autrement dit la profondeur de sa concavité.
[formule 7]





